Talk:Homology braid II (Ex)
(Created page with "<wikitex>; '''1)''' The diagram is composed of the exact sequences of the pair $(\widetilde W,\widetilde M)$, and of the triple $(\widetilde W,\widetilde M\cup\widetilde M',\...") |
|||
| Line 24: | Line 24: | ||
To repair this, put an additional minus sign on all boundary arrows | To repair this, put an additional minus sign on all boundary arrows | ||
landing in $H_\bullet(\widetilde M)$. | landing in $H_\bullet(\widetilde M)$. | ||
| + | |||
| + | '''2)''' | ||
| + | We have learned that $W$ is homotopy equivalent to $M\cup_{g|}D^{k+1}$. | ||
| + | Let $\tilde g|\colon S^k\to\widetilde M$ be a lift (ok if $k\ge2$) | ||
| + | If we pass to the universal cover of $M$, we are attaching a $\pi$-cell $\pi\times D^{k+1}$ | ||
| + | by $(\gamma,t)\mapsto\gamma(\tilde g(t))$. | ||
| + | Excision gives | ||
| + | $$H_i(\widetilde W,\widetilde M)\cong H_i(\widetilde M\cup_{\pi\times S^k}(\pi\times D^{k+1}),\widetilde M) | ||
| + | \cong \Z\pi H_i(D^{k+1},S^k).$$ | ||
| + | Similarly, swapping $W$ is homotopy equivalent to $M'\cup_{S^{n-k}}D^{n+1-k}$. | ||
| + | This gives the second assertion. | ||
--~~~~ | --~~~~ | ||
| − | |||
| − | |||
<wikitex> | <wikitex> | ||
Revision as of 08:58, 29 March 2012
1) The diagram is composed of the exact sequences of the pair 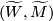 ,
and of the triple
,
and of the triple 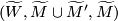 ,
and of the analogous sequences with
,
and of the analogous sequences with 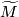 and
and 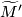 swapped.
Because
swapped.
Because 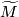 and
and 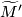 are disjoint, we have an isomorphism
are disjoint, we have an isomorphism
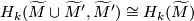 and another one with
and another one with 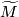 and
and 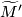 swapped. Both are implicit in the braid.
swapped. Both are implicit in the braid.
The squares that are half visible on the left and right hand side obviously commute. The upper triangles commute because of the following diagram,
![\displaystyle \xymatrix{ H_{i+1}(\widetilde W,\widetilde M) \ar[d] \ar[r]^{\partial} & H_i(\widetilde M) \ar[d]^{\cong} \ar[r] & H_i(\widetilde W) \ar[d] \\ H_{i+1}(\widetilde W,\widetilde M\cup\widetilde M') \ar[r]^{\partial} & H_i(\widetilde M\cup\widetilde M',\widetilde M') \ar[r] & H_i(\widetilde W,\widetilde M')}](/images/math/0/7/8/078863cf5a09b03d81ea4c5672c768e4.png)
The lower triangles work similarly.
The middle square only commutes up to sign:
let~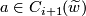 be a relative cycle in~
be a relative cycle in~ ,
so
,
so 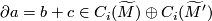 .
Then the upper path maps
.
Then the upper path maps ![[a]](/images/math/e/e/2/ee26865148f3cee59af1bcea11e37b66.png) to
to ![[b]](/images/math/3/f/b/3fb84b3642f24074408481146065340d.png) ,
and the lower path maps
,
and the lower path maps ![[a]](/images/math/e/e/2/ee26865148f3cee59af1bcea11e37b66.png) to
to ![[c]=-[b+\partial a]=-[b]](/images/math/f/8/7/f8798bc318fdc2ac570e14da2681e95a.png) .
To repair this, put an additional minus sign on all boundary arrows
landing in
.
To repair this, put an additional minus sign on all boundary arrows
landing in 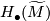 .
.
2)
We have learned that  is homotopy equivalent to
is homotopy equivalent to 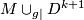 .
Let
.
Let 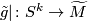 be a lift (ok if
be a lift (ok if 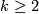 )
If we pass to the universal cover of
)
If we pass to the universal cover of  , we are attaching a
, we are attaching a  -cell
-cell 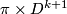 by
by 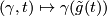 .
Excision gives
.
Excision gives
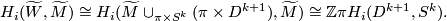
Similarly, swapping  is homotopy equivalent to
is homotopy equivalent to 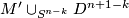 .
This gives the second assertion.
.
This gives the second assertion.
--~~~~