Talk:Homology braid II (Ex)
1) The diagram is composed of the exact sequences of the pair 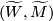 ,
and of the triple
,
and of the triple 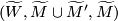 ,
and of the analogous sequences with
,
and of the analogous sequences with 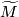 and
and 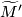 swapped.
Because
swapped.
Because 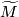 and
and 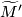 are disjoint, we have an isomorphism
are disjoint, we have an isomorphism
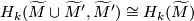 and another one with
and another one with 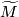 and
and 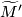 swapped. Both are implicit in the braid.
swapped. Both are implicit in the braid.
The squares that are half visible on the left and right hand side obviously commute. The upper triangles commute because of the following diagram,
![\displaystyle \xymatrix{ H_{i+1}(\widetilde W,\widetilde M) \ar[d] \ar[r]^{\partial} & H_i(\widetilde M) \ar[d]^{\cong} \ar[r] & H_i(\widetilde W) \ar[d] \\ H_{i+1}(\widetilde W,\widetilde M\cup\widetilde M') \ar[r]^{\partial} & H_i(\widetilde M\cup\widetilde M',\widetilde M') \ar[r] & H_i(\widetilde W,\widetilde M')}](/images/math/0/7/8/078863cf5a09b03d81ea4c5672c768e4.png)
The lower triangles work similarly.
The central square only commutes up to sign:
let~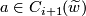 be a relative cycle in~
be a relative cycle in~ ,
so
,
so 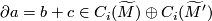 .
Then the upper path maps
.
Then the upper path maps ![[a]](/images/math/e/e/2/ee26865148f3cee59af1bcea11e37b66.png) to
to ![[b]](/images/math/3/f/b/3fb84b3642f24074408481146065340d.png) ,
and the lower path maps
,
and the lower path maps ![[a]](/images/math/e/e/2/ee26865148f3cee59af1bcea11e37b66.png) to
to ![[c]=-[b+\partial a]=-[b]](/images/math/f/8/7/f8798bc318fdc2ac570e14da2681e95a.png) .
To repair this, put an additional minus sign on all boundary arrows
landing in
.
To repair this, put an additional minus sign on all boundary arrows
landing in 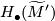 .
.
2)
We have learned that  is homotopy equivalent to
is homotopy equivalent to 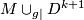 .
Let
.
Let 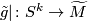 be a lift (ok if
be a lift (ok if 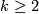 ).
If we pass to the universal cover of
).
If we pass to the universal cover of  , we are attaching a
, we are attaching a  -cell
-cell 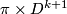 by
by 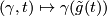 .
Excision gives
.
Excision gives
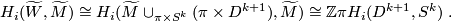
Similarly, swapping  is homotopy equivalent to
is homotopy equivalent to  .
This gives the second assertion.
.
This gives the second assertion.
3) By part 2, we get the following diagram.
![\displaystyle \xymatrix{ \Zz \pi H_{k+1}(D^{k+1},S^k) \ar[d]^{\cong} \ar[r]^{\cong} & \Zz \pi H_k(S^k) \ar[d]^{H_k\tilde g|}\\ H_{k+1}(\widetilde W,\widetilde M) \ar[r]^{\alpha} & H_k(\widetilde M).}](/images/math/a/c/a/aca5e9d115ddeea551b3109c491bcfda.png)
This proves part (a).
To prove part (b), we decompose  using the above braid as
using the above braid as
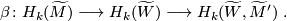
Now let  be a Morse function on
be a Morse function on  with
with 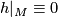 and
and 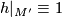 such that there is only one critical point of index
such that there is only one critical point of index  .
Fix a gradient vector field for
.
Fix a gradient vector field for  such that the stable and unstable disks are
exactly the core disk of the
such that the stable and unstable disks are
exactly the core disk of the  -handle and its dual.
We can multiply this vector field with a positive function such that the flow
-handle and its dual.
We can multiply this vector field with a positive function such that the flow  moves points
in
moves points
in  to
to 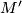 in time
in time  except in a small neighbourhood of the image of
except in a small neighbourhood of the image of 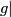 .
All this lifts to
.
All this lifts to 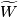 .
.
Now, let  be a smooth cycle in
be a smooth cycle in 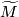 that is transversal to
that is transversal to 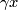 ,
which is the image of
,
which is the image of 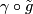 ,
for all
,
for all 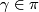 . The gradient flow moves
. The gradient flow moves  from
from  to
to 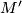 except in a small neighbourhood
of the image of
except in a small neighbourhood
of the image of 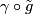 .
Hence,
.
Hence, 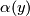 only depends on the intersections of
only depends on the intersections of  with the various~
with the various~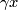 for
for 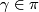 . This is the main step in the proof of (b).
. This is the main step in the proof of (b).