Stable classification of manifolds
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Two closed smooth manifolds  and
and  of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 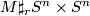 is diffeomorphic to
is diffeomorphic to 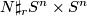 . By
. By 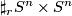 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
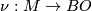 . We consider an
. We consider an  -factorization
-factorization 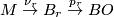
 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 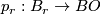 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 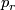 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 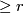 , and the map
, and the map 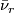 is an
is an  -equivalence.
-equivalence.
Definition 2.1. The fibre homotopy type of the fibration 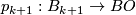 is an invariant of the map
is an invariant of the map  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 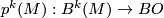 [Kreck1999].
[Kreck1999].
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
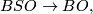
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  is the fibration
is the fibration
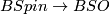
 admits a
admits a  -structure (if and only if the Stiefel-Whintey class
-structure (if and only if the Stiefel-Whintey class 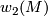 vanishes) and the fibration
vanishes) and the fibration
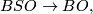
 does not admit a
does not admit a  structure. More generally, the normal
structure. More generally, the normal  -type of a Spin-manifold
-type of a Spin-manifold  is
is 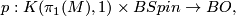
 is the composition of the projection to
is the composition of the projection to 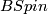 and the projection
and the projection 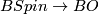 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 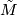 does not admit a
does not admit a  -structure, is
-structure, is 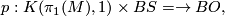
 is the composition of the projection to
is the composition of the projection to 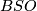 and the projection
and the projection 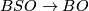 . The case where
. The case where 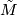 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of 4-manifolds.
doesn't, is treated in Stable classification of 4-manifolds.
If 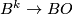
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001
 of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 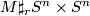 is diffeomorphic to
is diffeomorphic to 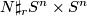 . By
. By 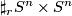 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
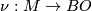 . We consider an
. We consider an  -factorization
-factorization 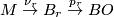
 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 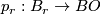 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 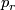 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 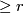 , and the map
, and the map 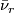 is an
is an  -equivalence.
-equivalence.
Definition 2.1. The fibre homotopy type of the fibration 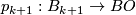 is an invariant of the map
is an invariant of the map  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 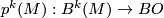 [Kreck1999].
[Kreck1999].
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
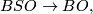
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  is the fibration
is the fibration
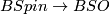
 admits a
admits a  -structure (if and only if the Stiefel-Whintey class
-structure (if and only if the Stiefel-Whintey class 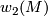 vanishes) and the fibration
vanishes) and the fibration
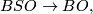
 does not admit a
does not admit a  structure. More generally, the normal
structure. More generally, the normal  -type of a Spin-manifold
-type of a Spin-manifold  is
is 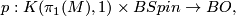
 is the composition of the projection to
is the composition of the projection to 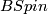 and the projection
and the projection 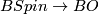 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 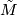 does not admit a
does not admit a  -structure, is
-structure, is 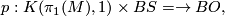
 is the composition of the projection to
is the composition of the projection to 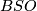 and the projection
and the projection 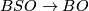 . The case where
. The case where 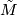 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of 4-manifolds.
doesn't, is treated in Stable classification of 4-manifolds.
If 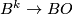
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001
 of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 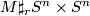 is diffeomorphic to
is diffeomorphic to 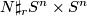 . By
. By 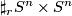 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
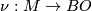 . We consider an
. We consider an  -factorization
-factorization 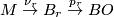
 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 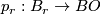 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 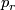 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 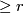 , and the map
, and the map 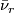 is an
is an  -equivalence.
-equivalence.
Definition 2.1. The fibre homotopy type of the fibration 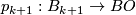 is an invariant of the map
is an invariant of the map  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 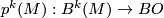 [Kreck1999].
[Kreck1999].
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
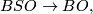
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  is the fibration
is the fibration
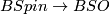
 admits a
admits a  -structure (if and only if the Stiefel-Whintey class
-structure (if and only if the Stiefel-Whintey class 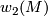 vanishes) and the fibration
vanishes) and the fibration
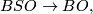
 does not admit a
does not admit a  structure. More generally, the normal
structure. More generally, the normal  -type of a Spin-manifold
-type of a Spin-manifold  is
is 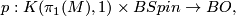
 is the composition of the projection to
is the composition of the projection to 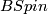 and the projection
and the projection 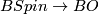 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 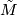 does not admit a
does not admit a  -structure, is
-structure, is 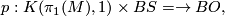
 is the composition of the projection to
is the composition of the projection to 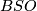 and the projection
and the projection 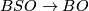 . The case where
. The case where 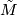 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of 4-manifolds.
doesn't, is treated in Stable classification of 4-manifolds.
If 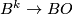
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001
 of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 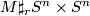 is diffeomorphic to
is diffeomorphic to 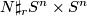 . By
. By 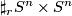 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
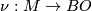 . We consider an
. We consider an  -factorization
-factorization 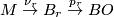
 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 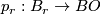 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 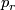 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 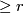 , and the map
, and the map 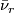 is an
is an  -equivalence.
-equivalence.
Definition 2.1. The fibre homotopy type of the fibration 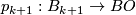 is an invariant of the map
is an invariant of the map  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 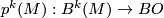 [Kreck1999].
[Kreck1999].
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
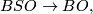
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  is the fibration
is the fibration
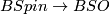
 admits a
admits a  -structure (if and only if the Stiefel-Whintey class
-structure (if and only if the Stiefel-Whintey class 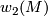 vanishes) and the fibration
vanishes) and the fibration
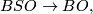
 does not admit a
does not admit a  structure. More generally, the normal
structure. More generally, the normal  -type of a Spin-manifold
-type of a Spin-manifold  is
is 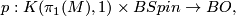
 is the composition of the projection to
is the composition of the projection to 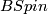 and the projection
and the projection 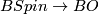 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 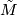 does not admit a
does not admit a  -structure, is
-structure, is 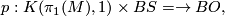
 is the composition of the projection to
is the composition of the projection to 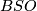 and the projection
and the projection 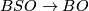 . The case where
. The case where 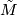 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of 4-manifolds.
doesn't, is treated in Stable classification of 4-manifolds.
If 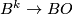
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001
 of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 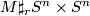 is diffeomorphic to
is diffeomorphic to 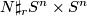 . By
. By 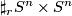 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
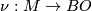 . We consider an
. We consider an  -factorization
-factorization 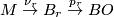
 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 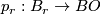 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 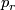 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 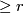 , and the map
, and the map 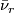 is an
is an  -equivalence.
-equivalence.
Definition 2.1. The fibre homotopy type of the fibration 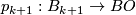 is an invariant of the map
is an invariant of the map  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 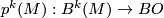 [Kreck1999].
[Kreck1999].
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
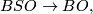
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  is the fibration
is the fibration
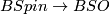
 admits a
admits a  -structure (if and only if the Stiefel-Whintey class
-structure (if and only if the Stiefel-Whintey class 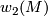 vanishes) and the fibration
vanishes) and the fibration
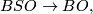
 does not admit a
does not admit a  structure. More generally, the normal
structure. More generally, the normal  -type of a Spin-manifold
-type of a Spin-manifold  is
is 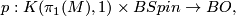
 is the composition of the projection to
is the composition of the projection to 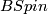 and the projection
and the projection 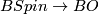 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 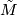 does not admit a
does not admit a  -structure, is
-structure, is 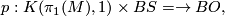
 is the composition of the projection to
is the composition of the projection to 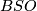 and the projection
and the projection 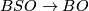 . The case where
. The case where 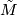 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of 4-manifolds.
doesn't, is treated in Stable classification of 4-manifolds.
If 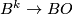
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001
 of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 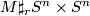 is diffeomorphic to
is diffeomorphic to 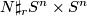 . By
. By 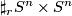 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Parametric connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
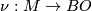 . We consider an
. We consider an  -factorization
-factorization 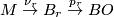
 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 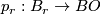 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 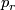 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 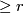 , and the map
, and the map 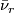 is an
is an  -equivalence.
-equivalence.
Definition 2.1. The fibre homotopy type of the fibration 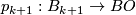 is an invariant of the map
is an invariant of the map  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 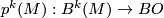 [Kreck1999].
[Kreck1999].
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
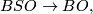
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  is the fibration
is the fibration
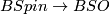
 admits a
admits a  -structure (if and only if the Stiefel-Whintey class
-structure (if and only if the Stiefel-Whintey class 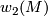 vanishes) and the fibration
vanishes) and the fibration
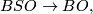
 does not admit a
does not admit a  structure. More generally, the normal
structure. More generally, the normal  -type of a Spin-manifold
-type of a Spin-manifold  is
is 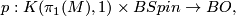
 is the composition of the projection to
is the composition of the projection to 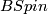 and the projection
and the projection 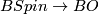 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 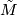 does not admit a
does not admit a  -structure, is
-structure, is 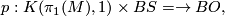
 is the composition of the projection to
is the composition of the projection to 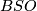 and the projection
and the projection 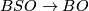 . The case where
. The case where 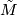 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of 4-manifolds.
doesn't, is treated in Stable classification of 4-manifolds.
If 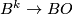
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001