Prime decomposition theorem in high dimensions
CarmenRovi (Talk | contribs) (→Problem) |
CarmenRovi (Talk | contribs) |
||
| Line 16: | Line 16: | ||
$$\star \mathbb{C}P^2 \sharp \star \mathbb{C}P^2 \cong \mathbb{C}P^2 \sharp \mathbb{C}P^2.$$ | $$\star \mathbb{C}P^2 \sharp \star \mathbb{C}P^2 \cong \mathbb{C}P^2 \sharp \mathbb{C}P^2.$$ | ||
{{endthm}} | {{endthm}} | ||
| + | ''Question'': Show that any prime decomposition of a topological $n$-manifold of dimension $n \geq 4$ is not unique. | ||
| + | |||
| + | This question was posed by Stefan Friedl at the [[:Category:MATRIX 2019 Interactions|MATRIX meeting on Interactions between high and low dimensional topology.]] | ||
</wikitex> | </wikitex> | ||
Revision as of 21:58, 8 January 2019
1 Problem
Every closed topological oriented manifold  has a prime decomposition
has a prime decomposition
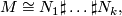
where the 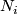 are prime manifolds.
Recall that a manifold is prime if for any decomposition as a connected
sum
are prime manifolds.
Recall that a manifold is prime if for any decomposition as a connected
sum 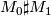 one of the summands
one of the summands  or
or  is homeomorphic to
is homeomorphic to  .
.
For  -manifolds, it was shown in [Milnor1962a] that the decomposition is unique.
For high-dimensional manifolds, there is no notion of prime decomposition of smooth manifolds, but there is a notion of prime decomposition for topological manifolds.
Nevertheless, the decomposition is not unique.
-manifolds, it was shown in [Milnor1962a] that the decomposition is unique.
For high-dimensional manifolds, there is no notion of prime decomposition of smooth manifolds, but there is a notion of prime decomposition for topological manifolds.
Nevertheless, the decomposition is not unique.
In [Kreck&Lück&Teichner1994] it is proven that a  -dimensional stable version of Kneser's conjecture on the splitting of three-manifolds as connected sums. The result clearly doesn't work non-stably in dimension
-dimensional stable version of Kneser's conjecture on the splitting of three-manifolds as connected sums. The result clearly doesn't work non-stably in dimension  and this paper gives some counterexamples. Another counterexample to the uniqueness of the decomposition is as follows.
and this paper gives some counterexamples. Another counterexample to the uniqueness of the decomposition is as follows.
Example 1.1.
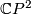 has a homotopy equivalent twin
has a homotopy equivalent twin 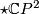 . The following decompositions provide a counterexample to uniqueness.
. The following decompositions provide a counterexample to uniqueness.
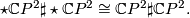
Question: Show that any prime decomposition of a topological  -manifold of dimension
-manifold of dimension 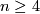 is not unique.
is not unique.
This question was posed by Stefan Friedl at the MATRIX meeting on Interactions between high and low dimensional topology.
2 References
- [Kreck&Lück&Teichner1994] M. Kreck, W. Lück and P. Teichner, Stable prime decompositions of four-manifolds, Prospects in topology, Princeton Univ. Press, Princeton, NJ (1995), 251–269. MR1368662 Zbl 0928.57019
- [Milnor1962a] J. Milnor, A unique decomposition theorem for
 -manifolds, Amer. J. Math. 84 (1962), 1–7. MR0142125 Zbl 0108.36501
-manifolds, Amer. J. Math. 84 (1962), 1–7. MR0142125 Zbl 0108.36501