Poincaré duality II (Ex)
From Manifold Atlas
(Difference between revisions)
Patrickorson (Talk | contribs) (Created page with "<wikitex>; For a simplicial complex $X$, define the front $p$-face of an $n$-simplex $\sigma = [v_0\ldots v_n]$ as $_p\sigma:=[v_0\ldots v_p]$ and the back $q$-face as $\sigma...") |
m |
||
| (One intermediate revision by one user not shown) | |||
| Line 3: | Line 3: | ||
The Alexander-Whitney diagonal approximation is given by | The Alexander-Whitney diagonal approximation is given by | ||
| − | $$ | + | $$\begin{aligned} |
| − | \tau: C_n(X) \to (C(X)\otimes C(X))_n | + | \tau: C_n(X) &\to (C(X)\otimes C(X))_n \\ |
| − | + | \sigma &\mapsto \sum_{p+q=n}{_p\sigma\otimes\sigma_q} | |
| + | \end{aligned} | ||
$$ | $$ | ||
and the partial evaluation map is defined as | and the partial evaluation map is defined as | ||
$$ | $$ | ||
| − | E: C^r(X)\otimes C_p(X)\otimes C_q(X) \to C_q(X) | + | \begin{aligned} |
| − | + | E: C^r(X)\otimes C_p(X)\otimes C_q(X) &\to C_q(X)\\ | |
| − | + | a\otimes z \otimes w &\mapsto \left\{ \begin{array}{cc} a(w)\otimes z, & r=q \\ | |
| − | a\otimes z \otimes w \mapsto \left\{ \begin{array}{cc} a(w)\otimes z, & r=q \\ | + | |
0, & \mathrm{otherwise} \end{array}\right. ~. | 0, & \mathrm{otherwise} \end{array}\right. ~. | ||
| + | \end{aligned} | ||
$$ | $$ | ||
Recall, we define the cap product on the chain level by $$a\cap z := E(a\otimes \tau(z))$$ and this descends to a well defined product on (co)homology. | Recall, we define the cap product on the chain level by $$a\cap z := E(a\otimes \tau(z))$$ and this descends to a well defined product on (co)homology. | ||
| Line 19: | Line 20: | ||
Consider $S^1$ as a simplicial complex with three $0$-simplices and three $1$-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map $$ -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)$$ thus verifying that $S^1$ has Poincaré duality. | Consider $S^1$ as a simplicial complex with three $0$-simplices and three $1$-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map $$ -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)$$ thus verifying that $S^1$ has Poincaré duality. | ||
</wikitex> | </wikitex> | ||
| − | == References == | + | <!-- == References == |
| − | {{#RefList:}} | + | {{#RefList:}} --> |
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises with solution]] | ||
Latest revision as of 14:56, 1 April 2012
For a simplicial complex  , define the front
, define the front  -face of an
-face of an  -simplex
-simplex ![\sigma = [v_0\ldots v_n]](/images/math/2/7/f/27f59f8d6be71b822333e8d85413a361.png) as
as ![_p\sigma:=[v_0\ldots v_p]](/images/math/1/e/2/1e29afd1ebf5c47cd088c03137c44d77.png) and the back
and the back  -face as
-face as ![\sigma_q := [v_{n-q}\ldots v_n].](/images/math/2/0/3/203c2a284924fa91ce13d37550fedcc4.png)
The Alexander-Whitney diagonal approximation is given by
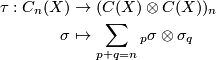
and the partial evaluation map is defined as
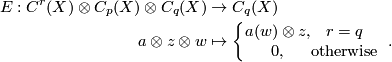
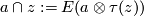
 as a simplicial complex with three
as a simplicial complex with three  -simplices and three
-simplices and three  -simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map
-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map ![\displaystyle -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)](/images/math/0/8/8/088bf75c548d58b59fdd0a562533782c.png)
 has Poincaré duality.
$-simplices and three X, define the front
has Poincaré duality.
$-simplices and three X, define the front  -face of an
-face of an  -simplex
-simplex ![\sigma = [v_0\ldots v_n]](/images/math/2/7/f/27f59f8d6be71b822333e8d85413a361.png) as
as ![_p\sigma:=[v_0\ldots v_p]](/images/math/1/e/2/1e29afd1ebf5c47cd088c03137c44d77.png) and the back
and the back  -face as
-face as ![\sigma_q := [v_{n-q}\ldots v_n].](/images/math/2/0/3/203c2a284924fa91ce13d37550fedcc4.png)
The Alexander-Whitney diagonal approximation is given by
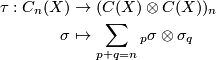
and the partial evaluation map is defined as
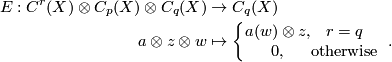
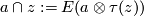
 as a simplicial complex with three
as a simplicial complex with three  -simplices and three
-simplices and three  -simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map
-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map ![\displaystyle -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)](/images/math/0/8/8/088bf75c548d58b59fdd0a562533782c.png)
 has Poincaré duality.
$-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map $$ -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)$$ thus verifying that $S^1$ has Poincaré duality.
== References ==
{{#RefList:}}
[[Category:Exercises]]X, define the front
has Poincaré duality.
$-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map $$ -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)$$ thus verifying that $S^1$ has Poincaré duality.
== References ==
{{#RefList:}}
[[Category:Exercises]]X, define the front  -face of an
-face of an  -simplex
-simplex ![\sigma = [v_0\ldots v_n]](/images/math/2/7/f/27f59f8d6be71b822333e8d85413a361.png) as
as ![_p\sigma:=[v_0\ldots v_p]](/images/math/1/e/2/1e29afd1ebf5c47cd088c03137c44d77.png) and the back
and the back  -face as
-face as ![\sigma_q := [v_{n-q}\ldots v_n].](/images/math/2/0/3/203c2a284924fa91ce13d37550fedcc4.png)
The Alexander-Whitney diagonal approximation is given by
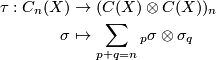
and the partial evaluation map is defined as
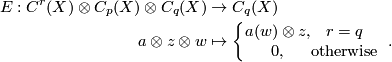
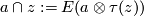
 as a simplicial complex with three
as a simplicial complex with three  -simplices and three
-simplices and three  -simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map
-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map ![\displaystyle -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)](/images/math/0/8/8/088bf75c548d58b59fdd0a562533782c.png)
 has Poincaré duality.
has Poincaré duality.