Poincaré duality II (Ex)
From Manifold Atlas
Revision as of 21:37, 19 March 2012 by Patrickorson (Talk | contribs)
For a simplicial complex  , define the front
, define the front  -face of an
-face of an  -simplex
-simplex ![\sigma = [v_0\ldots v_n]](/images/math/2/7/f/27f59f8d6be71b822333e8d85413a361.png) as
as ![_p\sigma:=[v_0\ldots v_p]](/images/math/1/e/2/1e29afd1ebf5c47cd088c03137c44d77.png) and the back
and the back  -face as
-face as ![\sigma_q := [v_{n-q}\ldots v_n].](/images/math/2/0/3/203c2a284924fa91ce13d37550fedcc4.png)
The Alexander-Whitney diagonal approximation is given by
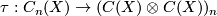
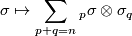
and the partial evaluation map is defined as
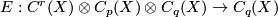
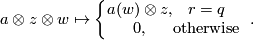
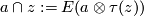
 as a simplicial complex with three
as a simplicial complex with three  -simplices and three
-simplices and three  -simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map
-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map ![\displaystyle -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)](/images/math/0/8/8/088bf75c548d58b59fdd0a562533782c.png)
 has Poincaré duality.
has Poincaré duality.
References
$-simplices and three X, define the front -face of an
-face of an  -simplex
-simplex ![\sigma = [v_0\ldots v_n]](/images/math/2/7/f/27f59f8d6be71b822333e8d85413a361.png) as
as ![_p\sigma:=[v_0\ldots v_p]](/images/math/1/e/2/1e29afd1ebf5c47cd088c03137c44d77.png) and the back
and the back  -face as
-face as ![\sigma_q := [v_{n-q}\ldots v_n].](/images/math/2/0/3/203c2a284924fa91ce13d37550fedcc4.png)
The Alexander-Whitney diagonal approximation is given by
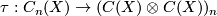
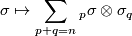
and the partial evaluation map is defined as
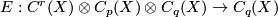
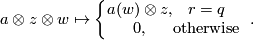
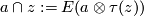
 as a simplicial complex with three
as a simplicial complex with three  -simplices and three
-simplices and three  -simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map
-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map ![\displaystyle -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)](/images/math/0/8/8/088bf75c548d58b59fdd0a562533782c.png)
 has Poincaré duality.
has Poincaré duality.
References
$-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map $$ -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)$$ thus verifying that $S^1$ has Poincaré duality. == References == {{#RefList:}} [[Category:Exercises]]X, define the front -face of an
-face of an  -simplex
-simplex ![\sigma = [v_0\ldots v_n]](/images/math/2/7/f/27f59f8d6be71b822333e8d85413a361.png) as
as ![_p\sigma:=[v_0\ldots v_p]](/images/math/1/e/2/1e29afd1ebf5c47cd088c03137c44d77.png) and the back
and the back  -face as
-face as ![\sigma_q := [v_{n-q}\ldots v_n].](/images/math/2/0/3/203c2a284924fa91ce13d37550fedcc4.png)
The Alexander-Whitney diagonal approximation is given by
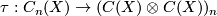
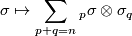
and the partial evaluation map is defined as
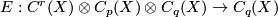
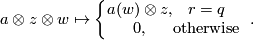
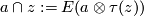
 as a simplicial complex with three
as a simplicial complex with three  -simplices and three
-simplices and three  -simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map
-simplices. Compute explicitly, using the Alexander-Whitney diagonal approximation, the map ![\displaystyle -\cap[S^1]: C^{1-*}(S^1) \to C_*(S^1)](/images/math/0/8/8/088bf75c548d58b59fdd0a562533782c.png)
 has Poincaré duality.
has Poincaré duality.