Talk:Poincaré duality II (Ex)

Note: There is a sign error in this solution to be fixed!! Give 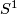$S^1$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}S^1$ the triangulation with 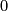$0$$0$-simplices 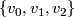$\{v_0,v_1,v_2\}$$\{v_0,v_1,v_2\}$ and $1$$1$-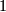simplices $\{[v_0,v_1], [v_1,v_2] , [v_2,v_0] \}$$\{[v_0,v_1], [v_1,v_2] , [v_2,v_0] \}$. Let us choose the fundamental class

$\displaystyle [S^1]=[v_0,v_1]\cup[v_1,v_2]\cup[v_2,v_0].$ $$\displaystyle [S^1]=[v_0,v_1]\cup[v_1,v_2]\cup[v_2,v_0].$$

The diagonal approximation $\tau$$\tau$ maps $[v_0,v_1]$$[v_0,v_1]$ to

$\displaystyle \begin{aligned} && \sum_{p+q=1} {_p[v_0,v_1]\otimes [v_0,v_1]_q} \\&=& {_0[v_0,v_1]}\otimes [v_0,v_1]_1 + {_1[v_0,v_1]}\otimes [v_0,v_1]_0 \\&=& \{v_0\}\otimes [v_0,v_1] + [v_0,v_1]\otimes\{v_1\}.\end{aligned}$ $$\displaystyle \begin{aligned} && \sum_{p+q=1} {_p[v_0,v_1]\otimes [v_0,v_1]_q} \\&=& {_0[v_0,v_1]}\otimes [v_0,v_1]_1 + {_1[v_0,v_1]}\otimes [v_0,v_1]_0 \\&=& \{v_0\}\otimes [v_0,v_1] + [v_0,v_1]\otimes\{v_1\}.\end{aligned}$$

Thus the diagonal approximation of the fundamental class $\tau([S^1])$$\tau([S^1])$ is

$\displaystyle \{v_0\}\otimes [v_0,v_1] + [v_0,v_1]\otimes\{v_1\}+ \{v_1\}\otimes [v_1,v_2] + [v_1,v_2]\otimes\{v_2\} + \{v_2\}\otimes [v_2,v_0] + [v_2,v_0]\otimes\{v_0\}.$ $$\displaystyle \{v_0\}\otimes [v_0,v_1] + [v_0,v_1]\otimes\{v_1\}+ \{v_1\}\otimes [v_1,v_2] + [v_1,v_2]\otimes\{v_2\} + \{v_2\}\otimes [v_2,v_0] + [v_2,v_0]\otimes\{v_0\}.$$

Capping with the fundamental class sends 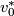$v_0^*$$v_0^*$ to

$\displaystyle \begin{aligned} && E(v_0^*\otimes\tau([S^1])) \\ &=& E(v_0^*\otimes ([v_2,v_0]\otimes\{v_0\}+ \mathrm{other}\;\mathrm{terms})) \\ &=& v_0^*(v_0)\otimes[v_2,v_0]\\ &=& [v_2,v_0]. \end{aligned}$ $$\displaystyle \begin{aligned} && E(v_0^*\otimes\tau([S^1])) \\ &=& E(v_0^*\otimes ([v_2,v_0]\otimes\{v_0\}+ \mathrm{other}\;\mathrm{terms})) \\ &=& v_0^*(v_0)\otimes[v_2,v_0]\\ &=& [v_2,v_0]. \end{aligned}$$

Similarly, $-\cap[S^1]$$-\cap[S^1]$ sends

$\displaystyle \begin{aligned} v_1^* &\mapsto& [v_0,v_1], \\ v_2^* &\mapsto& [v_1,v_2], \\ [v_0,v_1]^* &\mapsto& v_0, \\ [v_1,v_2]^* &\mapsto& v_1, \\ [v_2,v_0]^* &\mapsto& v_2. \end{aligned}$ $$\displaystyle \begin{aligned} v_1^* &\mapsto& [v_0,v_1], \\ v_2^* &\mapsto& [v_1,v_2], \\ [v_0,v_1]^* &\mapsto& v_0, \\ [v_1,v_2]^* &\mapsto& v_1, \\ [v_2,v_0]^* &\mapsto& v_2. \end{aligned}$$

Thus we obtain the chain equivalence

$\displaystyle \xymatrix{ <v_0^*,v_1^*,v_2^*> = C^0(S^1)\ar[rr]^-{(-\cap[S^1])_1} \ar[d]_{\delta} && C_1(S^1)=<[v_0,v_1],[v_1,v_2],[v_2,v_0]> \ar[d]^{d} \\ <[v_0,v_1]^*,[v_1,v_2]^*,[v_2,v_0]^*>=C^1(S^1) \ar[rr]^-{(-\cap[S^1])_0} && C_0(S^1)=<v_0,v_1,v_2>}$

Where

$\displaystyle (-\cap[S^1])_1 = \left( \begin{array}{ccc}0&1&0\\0&0&1\\1&0&0 \end{array}\right),\quad(-\cap[S^1])_0 = \left( \begin{array}{ccc}1&0&0\\0&1&0\\0&0&1 \end{array}\right),\quad d= \left( \begin{array}{ccc}-1&0&1\\1&-1&0\\0&1&-1 \end{array}\right),\quad \delta = \left( \begin{array}{ccc}-1&1&0\\0&-1&1\\1&0&-1 \end{array}\right).$ $$\displaystyle (-\cap[S^1])_1 = \left( \begin{array}{ccc}0&1&0\\0&0&1\\1&0&0 \end{array}\right),\quad(-\cap[S^1])_0 = \left( \begin{array}{ccc}1&0&0\\0&1&0\\0&0&1 \end{array}\right),\quad d= \left( \begin{array}{ccc}-1&0&1\\1&-1&0\\0&1&-1 \end{array}\right),\quad \delta = \left( \begin{array}{ccc}-1&1&0\\0&-1&1\\1&0&-1 \end{array}\right).$$

Note: this doesn't quite work - this is not a chain map, composing one way gives minus the composition the other way. Fixing the sign error we can take the inverse permutation matrices as the chain inverse.