Plumbing (Ex)
m |
m |
||
| (8 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | The exercises below are about plumbing manifolds. For the details of the construction, see the page [[Plumbing]] | + | The exercises below are about plumbing manifolds. For the details of the construction, see the page [[Plumbing]]. |
| − | + | ||
| − | + | ||
| − | Starting from the dijoint union of the total spaces $E_i$ we form | + | In this page we use slightly different notation. For $i = 1, \dots, n$ let |
| + | $$ \zeta_i \colon E_i \to S^q_i$$ | ||
| + | be an oriented $D^{q}$-bundle over $S^q$. Let $G$ be a graph with verticies $\{v_1, \dots, v_k \}$. | ||
| + | |||
| + | Starting from the dijoint union of the total spaces $E_i$ we form the plumbing manifold $X(G; \{\zeta_i\}$ as follows: given an edge in $G$ connecting $v_i$ and $v_j$, for $k = i$ and $j$, let $x_k \in E_k$ and let $D^{q} \times D^{q} \subseteq E_k$ be a neighbourhood of $x_k$, such that $D^{q} \times \{0\}\subseteq S^q_k$ and such that $y \times D^{q}$ if the fiber of $E_k \to S^q_k$. Let $h_{\pm}: D^{q} \rightarrow D^{q}$ and $k_{\pm}: D^{q} \rightarrow D^{q}$ be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing $E_i \diamond E_j$ of $E_i$ and $E_j$ at $x_i$ and $x_j$ by taking $E_i \sqcup E_j$ and identifying $D^q \times D^q \subset E_i$ and $D^q \times D^q \subset E_j$ via | ||
$$I_\pm(x,y)=(k_{\pm}(y), h_{\pm}(x)).$$ | $$I_\pm(x,y)=(k_{\pm}(y), h_{\pm}(x)).$$ | ||
Proceeding in this way for each edge of $G$ we obtain the plumbing manifold | Proceeding in this way for each edge of $G$ we obtain the plumbing manifold | ||
| Line 10: | Line 12: | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
| − | Let $X = X(G; \{\ | + | Let $X = X(G; \{\zeta_i \})$ be connected. Show the following: |
#$\pi_1(\partial X)\cong\pi_1(X)$ is free. | #$\pi_1(\partial X)\cong\pi_1(X)$ is free. | ||
| − | #$H_i(\partial X)=H_i(X)=0$ for $1<i< | + | #$H_i(\partial X)=H_i(X)=0$ for $1<i<q-1$ |
{{endthm}} | {{endthm}} | ||
{{beginrem|Hint}} | {{beginrem|Hint}} | ||
| − | The statement is trivial for $X$, since $X$ is homotopy equivalent to a wedge of 1-spheres and $ | + | The statement is trivial for $X$, since $X$ is homotopy equivalent to a wedge of 1-spheres and $q$-spheres. Now use van Kampen's theorem for $\pi_1(\partial X)$ and for $H_i(\partial X)$ use the Mayer-Vietories Sequence with $\partial E_i\backslash (D_i^q\times S^{q-1})$ and show that all components involved are $(q-2)$ connected. |
{{endrem}} | {{endrem}} | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
| − | Choose $S^1\subseteq \partial X$ representing a generator of $\pi_1(\partial X)$ and let $V$ be the trace of a surgery on this $S^1$. Define $X':=X\cup_{\partial X}V$. Show | + | Choose $S^1\subseteq \partial X$ representing a generator of $\pi_1(\partial X)$ and let $V$ be the trace of a surgery on this $S^1$. Define $X':=X\cup_{\partial X}V$. Show the following: |
| − | #$H_i(X')\cong H_i(X)$ for $i\neq 1$ | + | #$H_i(X')\cong H_i(X)$ for $i\neq 1$. |
| − | #$H_i(\partial X')\cong H_i(\partial X)$ for $1<i<2q-2$ | + | #$H_i(\partial X')\cong H_i(\partial X)$ for $1<i<2q-2$. |
{{beginrem|Hint}} | {{beginrem|Hint}} | ||
For (1) use the long exact sequence of the pair $(X',X)$ and $X'\simeq X\cup D^2$. For (2) use the long exact sequence of the pair $(V,\partial X')$ as well as Poincaré Duality and the Universal Coefficient Theorem. | For (1) use the long exact sequence of the pair $(X',X)$ and $X'\simeq X\cup D^2$. For (2) use the long exact sequence of the pair $(V,\partial X')$ as well as Poincaré Duality and the Universal Coefficient Theorem. | ||
{{endrem}} | {{endrem}} | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
| − | Assume now | + | Assume now that each bundle $\zeta_i$ is some multiple of $\tau_{S^q}$, the unit disc bundle of the tangent bundle of the $q$-sphere. Show that there is a degree 1 normal map $(f,b),f:(X',\partial X')\rightarrow (D^{2q},S^{2q-1})$. |
{{endthm}} | {{endthm}} | ||
{{beginrem|Hint}} | {{beginrem|Hint}} | ||
| − | Use that $X$ is homotopy equivalent to a wedge of 1-spheres and q-spheres and that the tangent bundle of $X$ is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of $(X,\partial X)\subseteq (D^{2q+k},S^{2q+k-1})$ is trivial for $k$ large. Then show that the map can be extend over $V$. | + | Use that $X$ is homotopy equivalent to a wedge of 1-spheres and $q$-spheres and that the tangent bundle of $X$ is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of $(X,\partial X)\subseteq (D^{2q+k},S^{2q+k-1})$ is trivial for $k$ large. Then show that the map can be extend over $V$. |
{{endrem}} | {{endrem}} | ||
| + | The exercises and hints on this page were sent by Fabian Hebestreit, Daniel Kasprowski and Christoph Winges. | ||
</wikitex> | </wikitex> | ||
| − | == References == | + | <!-- == References == |
| − | {{#RefList:}} | + | {{#RefList:}} --> |
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises without solution]] | ||
Latest revision as of 14:55, 1 April 2012
The exercises below are about plumbing manifolds. For the details of the construction, see the page Plumbing.
In this page we use slightly different notation. For 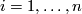 let
let
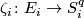
be an oriented 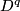 -bundle over
-bundle over 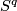 . Let
. Let  be a graph with verticies
be a graph with verticies  .
.
Starting from the dijoint union of the total spaces 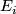 we form the plumbing manifold
we form the plumbing manifold 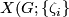 as follows: given an edge in
as follows: given an edge in  connecting
connecting 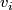 and
and 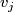 , for
, for 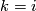 and
and  , let
, let 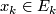 and let
and let 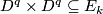 be a neighbourhood of
be a neighbourhood of 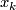 , such that
, such that 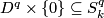 and such that
and such that 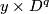 if the fiber of
if the fiber of 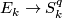 . Let
. Let 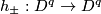 and
and 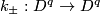 be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing
be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing 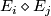 of
of 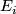 and
and 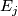 at
at 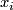 and
and 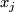 by taking
by taking 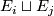 and identifying
and identifying 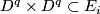 and
and 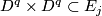 via
via
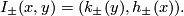
Proceeding in this way for each edge of  we obtain the plumbing manifold
we obtain the plumbing manifold
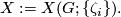
Exercise 0.1.
Let 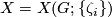 be connected. Show the following:
be connected. Show the following:
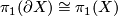 is free.
is free.
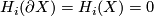 for
for 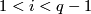
Hint 0.2.
The statement is trivial for  , since
, since  is homotopy equivalent to a wedge of 1-spheres and
is homotopy equivalent to a wedge of 1-spheres and  -spheres. Now use van Kampen's theorem for
-spheres. Now use van Kampen's theorem for 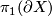 and for
and for 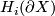 use the Mayer-Vietories Sequence with
use the Mayer-Vietories Sequence with 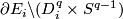 and show that all components involved are
and show that all components involved are 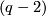 connected.
connected.
Exercise 0.3.
Choose 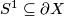 representing a generator of
representing a generator of 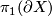 and let
and let  be the trace of a surgery on this
be the trace of a surgery on this  . Define
. Define 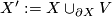 . Show the following:
. Show the following:
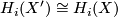 for
for 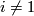 .
.
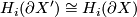 for
for 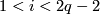 .
.
Hint 0.4.
For (1) use the long exact sequence of the pair 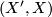 and
and 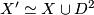 . For (2) use the long exact sequence of the pair
. For (2) use the long exact sequence of the pair 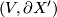 as well as Poincaré Duality and the Universal Coefficient Theorem.
as well as Poincaré Duality and the Universal Coefficient Theorem.
Exercise 0.5.
Assume now that each bundle 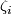 is some multiple of
is some multiple of 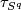 , the unit disc bundle of the tangent bundle of the
, the unit disc bundle of the tangent bundle of the  -sphere. Show that there is a degree 1 normal map
-sphere. Show that there is a degree 1 normal map 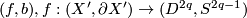 .
.
Hint 0.6.
Use that  is homotopy equivalent to a wedge of 1-spheres and
is homotopy equivalent to a wedge of 1-spheres and  -spheres and that the tangent bundle of
-spheres and that the tangent bundle of  is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of
is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of 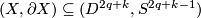 is trivial for
is trivial for  large. Then show that the map can be extend over
large. Then show that the map can be extend over  .
.
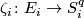
be an oriented 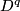 -bundle over
-bundle over 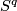 . Let
. Let  be a graph with verticies
be a graph with verticies  .
.
Starting from the dijoint union of the total spaces 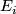 we form the plumbing manifold
we form the plumbing manifold 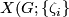 as follows: given an edge in
as follows: given an edge in  connecting
connecting 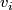 and
and 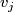 , for
, for 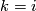 and
and  , let
, let 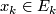 and let
and let 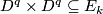 be a neighbourhood of
be a neighbourhood of 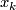 , such that
, such that 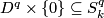 and such that
and such that 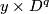 if the fiber of
if the fiber of 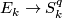 . Let
. Let 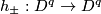 and
and 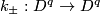 be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing
be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing 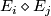 of
of 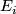 and
and 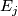 at
at 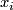 and
and 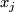 by taking
by taking 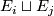 and identifying
and identifying 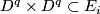 and
and 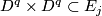 via
via
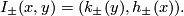
Proceeding in this way for each edge of  we obtain the plumbing manifold
we obtain the plumbing manifold
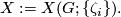
Exercise 0.1.
Let 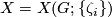 be connected. Show the following:
be connected. Show the following:
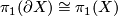 is free.
is free.
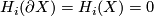 for
for 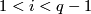
Hint 0.2.
The statement is trivial for  , since
, since  is homotopy equivalent to a wedge of 1-spheres and
is homotopy equivalent to a wedge of 1-spheres and  -spheres. Now use van Kampen's theorem for
-spheres. Now use van Kampen's theorem for 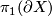 and for
and for 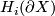 use the Mayer-Vietories Sequence with
use the Mayer-Vietories Sequence with 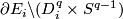 and show that all components involved are
and show that all components involved are 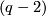 connected.
connected.
Exercise 0.3.
Choose 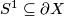 representing a generator of
representing a generator of 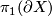 and let
and let  be the trace of a surgery on this
be the trace of a surgery on this  . Define
. Define 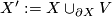 . Show the following:
. Show the following:
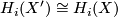 for
for 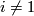 .
.
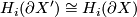 for
for 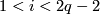 .
.
Hint 0.4.
For (1) use the long exact sequence of the pair 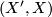 and
and 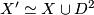 . For (2) use the long exact sequence of the pair
. For (2) use the long exact sequence of the pair 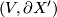 as well as Poincaré Duality and the Universal Coefficient Theorem.
as well as Poincaré Duality and the Universal Coefficient Theorem.
Exercise 0.5.
Assume now that each bundle 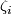 is some multiple of
is some multiple of 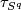 , the unit disc bundle of the tangent bundle of the
, the unit disc bundle of the tangent bundle of the  -sphere. Show that there is a degree 1 normal map
-sphere. Show that there is a degree 1 normal map 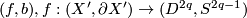 .
.
Hint 0.6.
Use that  is homotopy equivalent to a wedge of 1-spheres and
is homotopy equivalent to a wedge of 1-spheres and  -spheres and that the tangent bundle of
-spheres and that the tangent bundle of  is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of
is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of 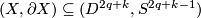 is trivial for
is trivial for  large. Then show that the map can be extend over
large. Then show that the map can be extend over  .
.
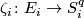
be an oriented 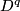 -bundle over
-bundle over 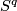 . Let
. Let  be a graph with verticies
be a graph with verticies  .
.
Starting from the dijoint union of the total spaces 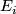 we form the plumbing manifold
we form the plumbing manifold 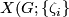 as follows: given an edge in
as follows: given an edge in  connecting
connecting 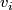 and
and 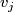 , for
, for 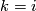 and
and  , let
, let 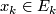 and let
and let 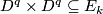 be a neighbourhood of
be a neighbourhood of 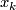 , such that
, such that 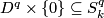 and such that
and such that 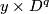 if the fiber of
if the fiber of 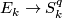 . Let
. Let 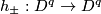 and
and 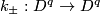 be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing
be orientation preserving (resp. reversing) diffeomorphisms. We define the plumbing 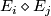 of
of 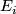 and
and 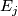 at
at 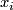 and
and 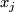 by taking
by taking 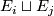 and identifying
and identifying 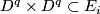 and
and 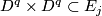 via
via
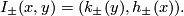
Proceeding in this way for each edge of  we obtain the plumbing manifold
we obtain the plumbing manifold
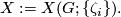
Exercise 0.1.
Let 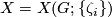 be connected. Show the following:
be connected. Show the following:
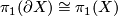 is free.
is free.
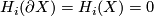 for
for 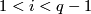
Hint 0.2.
The statement is trivial for  , since
, since  is homotopy equivalent to a wedge of 1-spheres and
is homotopy equivalent to a wedge of 1-spheres and  -spheres. Now use van Kampen's theorem for
-spheres. Now use van Kampen's theorem for 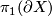 and for
and for 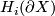 use the Mayer-Vietories Sequence with
use the Mayer-Vietories Sequence with 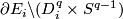 and show that all components involved are
and show that all components involved are 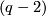 connected.
connected.
Exercise 0.3.
Choose 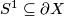 representing a generator of
representing a generator of 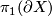 and let
and let  be the trace of a surgery on this
be the trace of a surgery on this  . Define
. Define 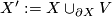 . Show the following:
. Show the following:
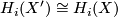 for
for 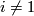 .
.
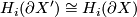 for
for 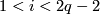 .
.
Hint 0.4.
For (1) use the long exact sequence of the pair 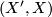 and
and 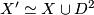 . For (2) use the long exact sequence of the pair
. For (2) use the long exact sequence of the pair 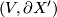 as well as Poincaré Duality and the Universal Coefficient Theorem.
as well as Poincaré Duality and the Universal Coefficient Theorem.
Exercise 0.5.
Assume now that each bundle 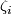 is some multiple of
is some multiple of 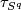 , the unit disc bundle of the tangent bundle of the
, the unit disc bundle of the tangent bundle of the  -sphere. Show that there is a degree 1 normal map
-sphere. Show that there is a degree 1 normal map 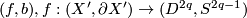 .
.
Hint 0.6.
Use that  is homotopy equivalent to a wedge of 1-spheres and
is homotopy equivalent to a wedge of 1-spheres and  -spheres and that the tangent bundle of
-spheres and that the tangent bundle of  is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of
is stabily trivial (since it is so on every component of the wedge), so that the normal bundle of 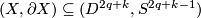 is trivial for
is trivial for  large. Then show that the map can be extend over
large. Then show that the map can be extend over  .
.