Plumbing
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
Plumbing is a gluing construction which takes as input some disk bundles over manifolds (frequently just spheres)
with  -dimensional total space and produces another
-dimensional total space and produces another  -manifold with boundary.
It identifies fibers of one bundle with disks in the base manifold of the other bundle and vice versa.
-manifold with boundary.
It identifies fibers of one bundle with disks in the base manifold of the other bundle and vice versa.
[edit] 2 Construction
As special case of the following construction goes back at least to [Milnor1959].
Let 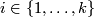 , let
, let 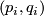 be pairs of positive integers such that
be pairs of positive integers such that 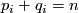 and let
and let 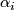 be an oriented
be an oriented 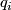 -dimensional vector bundle over the
-dimensional vector bundle over the 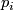 -dimensional oriented manifold
-dimensional oriented manifold 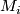 . We consider the corresponding disk bundles
. We consider the corresponding disk bundles
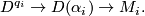
Let  be a graph with vertices
be a graph with vertices  such that the edge set between
such that the edge set between 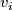 and
and 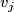 , is non-empty only if
, is non-empty only if 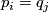 and
and 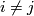 . We choose disjoint disks
. We choose disjoint disks 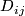 in
in 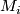 (one for each edge incident to
(one for each edge incident to 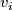 )
and trivializations
)
and trivializations 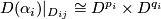 (preserving orientations).
Finally we form the manifold
(preserving orientations).
Finally we form the manifold 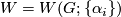 from the disjoint union of the
from the disjoint union of the 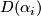 by identifying, for each edge of
by identifying, for each edge of  , the corresponding
, the corresponding 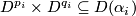 and
and
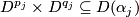 with the standard diffeomorphism
with the standard diffeomorphism 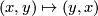 , which interchanges
base and fiber of the two bundles.
, which interchanges
base and fiber of the two bundles.
The manifold  is the result of the plumbing, often one is mainly interested in its boundary
is the result of the plumbing, often one is mainly interested in its boundary 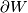 .
.
[edit] 3 Invariants
...
[edit] 4 An important special case
If  is simply connected and all the base manifolds are spheres then
is simply connected and all the base manifolds are spheres then
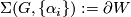
is often a homotopy sphere. We establish some notation for graphs, bundles and define
- let
 denote the graph with two vertices and one edge connecting them and define
denote the graph with two vertices and one edge connecting them and define 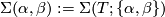 ,
,
- let
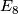 denote the
denote the 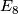 -graph,
-graph,
- let
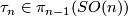 denote the tangent bundle of the
denote the tangent bundle of the  -sphere,
-sphere,
- let
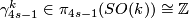 ,
, 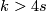 , denote a generator,
, denote a generator,
- let
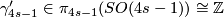 , denote a generator:
, denote a generator:
- let
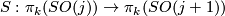 be the suspension homomorphism,
be the suspension homomorphism,
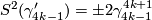 for
for 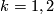 and
and 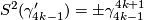 for
for 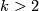 ,
,
- let
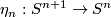 be essential.
be essential.
The plumbing construction can be used to produce exotic spheres:
-
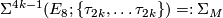 , the Milnor sphere, generates
, the Milnor sphere, generates  ,
, 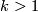 .
.
-
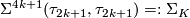 , the Kervaire sphere, generates
, the Kervaire sphere, generates 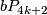 .
.
-
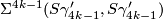 is the inverse of the Milnor sphere for
is the inverse of the Milnor sphere for 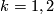 .
.
- For general
 ,
, 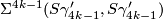 is exotic.
is exotic.
- For general
-
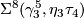 , generates
, generates 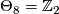 .
.
-
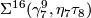 , generates
, generates 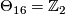 .
.
[edit] 5 References
- [Milnor1959] J. Milnor, Differentiable structures on spheres, Amer. J. Math. 81 (1959), 962–972. MR0110107 (22 #990) Zbl 0111.35501