Middle-dimensional surgery kernel (Ex)
(Created page with "<wikitex>; The goal of the following exercise is to prove the following statement which will be indispensible in defining the surgery obstruction. {{beginthm|Proposition}} ...") |
m |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | The goal of | + | The goal of this exercise is to prove the following statement which will be indispensible in defining the surgery obstruction. |
{{beginthm|Proposition}} Let $f:M\rightarrow X$ be a degree 1 normal map from a $2k$-dimensional (resp. $(2k+1)$-dimensional manifold to a geometric Poincaré complex, inducing the isomorphism $f_\ast:\pi_1(M)\cong\pi_1(X)=:\pi$. Denote by $K_i(M)=K_i(\widetilde{M})$ the homology surgery kernel $\mathbb{Z}[\pi]$-module. If $f$ is $k$-connected the kernel module $K_k(M)$ is finitely generated and stably free. | {{beginthm|Proposition}} Let $f:M\rightarrow X$ be a degree 1 normal map from a $2k$-dimensional (resp. $(2k+1)$-dimensional manifold to a geometric Poincaré complex, inducing the isomorphism $f_\ast:\pi_1(M)\cong\pi_1(X)=:\pi$. Denote by $K_i(M)=K_i(\widetilde{M})$ the homology surgery kernel $\mathbb{Z}[\pi]$-module. If $f$ is $k$-connected the kernel module $K_k(M)$ is finitely generated and stably free. | ||
{{endthm|Proposition}} | {{endthm|Proposition}} | ||
| − | The statement essentially follows from the technical lemma which | + | The statement essentially follows from the technical lemma which you are asked to prove. |
| + | {{beginthm|Lemma|{{citeD|Ranicki2002|Lemma 10.26}}}} | ||
Let $R$ be a ring with involution and $C=C_\ast$ a finite chain complex of finitely generated projective (left) $R$-modules. | Let $R$ be a ring with involution and $C=C_\ast$ a finite chain complex of finitely generated projective (left) $R$-modules. | ||
| Line 12: | Line 13: | ||
'''2)''' If in addition for $j>n$, $H^j(C)=0$ for the same integer $n$ then $H_n(C)$ and $H^n(C)$ are dual, and there are isomorphisms$$H_n(C)\oplus\sum_{i\in\mathbb{Z}}C_{n+2i+1}\cong\sum_{j\in\mathbb{Z}}C_{n+2j}, $$$$H^n(C)\oplus\sum_{i\in\mathbb{Z}}C^{n+2i+1}\cong\sum_{j\in\mathbb{Z}}C^{n+2j},$$where under further assumption that $C$ is a chain complex of free modules, the latter isomorphism implies that $H_n(C)$ and $H^n(C)$ are stably free. | '''2)''' If in addition for $j>n$, $H^j(C)=0$ for the same integer $n$ then $H_n(C)$ and $H^n(C)$ are dual, and there are isomorphisms$$H_n(C)\oplus\sum_{i\in\mathbb{Z}}C_{n+2i+1}\cong\sum_{j\in\mathbb{Z}}C_{n+2j}, $$$$H^n(C)\oplus\sum_{i\in\mathbb{Z}}C^{n+2i+1}\cong\sum_{j\in\mathbb{Z}}C^{n+2j},$$where under further assumption that $C$ is a chain complex of free modules, the latter isomorphism implies that $H_n(C)$ and $H^n(C)$ are stably free. | ||
| + | {{endthm|Lemma}} | ||
| − | The proposition is given as lemma 4.19 in {{citeD|Lück2001}}, however the proof is incomplete. Alternatively a good proof can be found in {{citeD|Wall1999}} and a more detailed one in | + | The proposition is given as lemma 4.19 in {{citeD|Lück2001}}, however the proof is incomplete. Alternatively a good proof can be found in {{citeD|Wall1999}} and a more detailed one in {{citeD|Ranicki2002}}. |
</wikitex> | </wikitex> | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
Revision as of 10:40, 19 March 2012
The goal of this exercise is to prove the following statement which will be indispensible in defining the surgery obstruction.
Proposition 0.1. Let 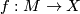 be a degree 1 normal map from a
be a degree 1 normal map from a 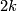 -dimensional (resp.
-dimensional (resp. 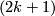 -dimensional manifold to a geometric Poincaré complex, inducing the isomorphism
-dimensional manifold to a geometric Poincaré complex, inducing the isomorphism 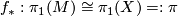 . Denote by
. Denote by 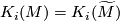 the homology surgery kernel
the homology surgery kernel ![\mathbb{Z}[\pi]](/images/math/5/3/9/5393263cfc1a4eb9ce95b62982af4354.png) -module. If
-module. If  is
is  -connected the kernel module
-connected the kernel module 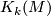 is finitely generated and stably free.
is finitely generated and stably free.
The statement essentially follows from the technical lemma which you are asked to prove.
Lemma 0.2 [Ranicki2002, Lemma 10.26].
Let  be a ring with involution and
be a ring with involution and 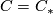 a finite chain complex of finitely generated projective (left)
a finite chain complex of finitely generated projective (left)  -modules.
-modules.
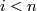 ,
, 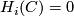 for some integer
for some integer  then the
then the  -module
-module 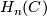 is finitely generated and
is finitely generated and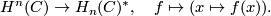
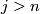 ,
, 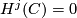 for the same integer
for the same integer  then
then 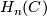 and
and 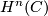 are dual, and there are isomorphisms
are dual, and there are isomorphisms
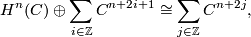
 is a chain complex of free modules, the latter isomorphism implies that
is a chain complex of free modules, the latter isomorphism implies that 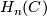 and
and 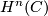 are stably free.
are stably free.
The proposition is given as lemma 4.19 in [Lück2001], however the proof is incomplete. Alternatively a good proof can be found in [Wall1999] and a more detailed one in [Ranicki2002].