Talk:Middle-dimensional surgery kernel (Ex)
First a little lemma:
Let 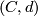 be a chain complex with
be a chain complex with 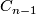 projective,
projective, 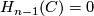 and
and 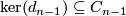 a direct summand. Then also
a direct summand. Then also 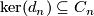 is a direct summand.
is a direct summand.
Proof:
Note that 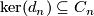 is a direct summand iff the sequence
is a direct summand iff the sequence
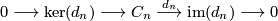
splits. By exactness at 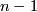 however, we have
however, we have 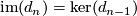 which is projective, being a direct summand of a projective module.
which is projective, being a direct summand of a projective module.
ad(1): Iterating the lemma we find that 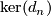 is a direct summand of
is a direct summand of 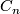 if the same statement holds for some lower
if the same statement holds for some lower  . However, eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module
. However, eventually both terms are zero, since the complex is finite. Being a direct summand in a finitely generated module 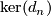 is then itself finitely generated, and hence also
is then itself finitely generated, and hence also 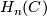 . The second assertion follows immediately from the universal coefficient theorem.
. The second assertion follows immediately from the universal coefficient theorem.
Comment: The second assertion does not follow from the universal coefficient theorem since the unversal coefficient theorem does not hold in this generality. R is an arbitrary ring with involution!
Before addressing (2) we will prove the following:
Proposition:
Under the assumptions of (2) there exist a chain map 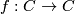 with
with 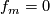 for
for 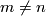 and
and 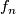 the projection onto a direct summand
the projection onto a direct summand  of
of 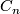 isomorphic to
isomorphic to  and such that
and such that  is chain homotopy equivalent to the identity on
is chain homotopy equivalent to the identity on  .
.
In (1) it was proved that 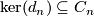 is a direct summand. The chain complex
is a direct summand. The chain complex 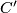 defined as
defined as
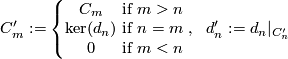
is again finitely generated and degreewise projective. The inclusion 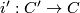 induces an isomorphism on homology and since all occurring modules are projective is a chain homotopy equivalence. We can choose a projection
induces an isomorphism on homology and since all occurring modules are projective is a chain homotopy equivalence. We can choose a projection 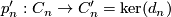 with
with 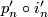 the identity on
the identity on 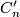 . Now extend this to a chain map
. Now extend this to a chain map 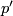 by identity maps on the one side and zero maps on the other and note that
by identity maps on the one side and zero maps on the other and note that 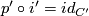 . Since
. Since 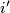 is a chain homotopy equivalence this implies that
is a chain homotopy equivalence this implies that 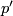 is a chain homotopy inverse of
is a chain homotopy inverse of 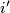 .
.
By assumption 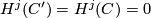 for
for 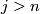 and since
and since 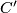 is finitely generated and degreewise projective so is
is finitely generated and degreewise projective so is 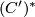 . Thus as before
. Thus as before 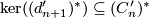 is a direct summand. Hence for the chain complex
is a direct summand. Hence for the chain complex 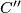 concentrated in degree
concentrated in degree  with
with 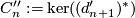 , the inclusion
, the inclusion 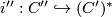 is a chain homotopy equivalence. We can again choose a projection
is a chain homotopy equivalence. We can again choose a projection 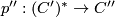 such that
such that 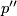 is an inverse of
is an inverse of 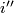 and
and 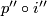 is the identity on
is the identity on 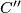 .
.
Putting this together we have chain homotopy equivalences 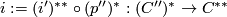 and
and 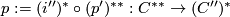 with
with  a chain homotopy inverse of
a chain homotopy inverse of  and
and 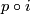 the identity on
the identity on 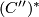 .
.
Since for 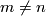 we have
we have 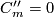 , also
, also 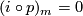 in dimensions
in dimensions 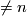 and because
and because 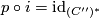 the map
the map 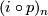 is a projection onto a direct summand
is a projection onto a direct summand  of
of  . Since
. Since 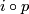 induces an isomorphism in homology
induces an isomorphism in homology  has to be isomorphic to
has to be isomorphic to 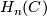 .
Upon identification of
.
Upon identification of 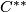 with
with  the proposition is proved.
the proposition is proved.
ad(2):
Choose a chain homotopy between the chain map
between the chain map  from the propsition above and the identity on
from the propsition above and the identity on  . We can choose
. We can choose  such that
such that 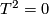 (???). Now for
(???). Now for 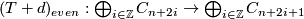 and
and 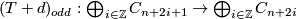 the composition
the composition 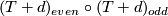 is the identity on
is the identity on 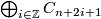 because
because 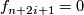 for all
for all 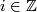 . And the composition
. And the composition 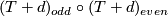 is the identity on
is the identity on 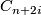 for
for 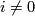 and the projection onto a complement of
and the projection onto a complement of  in degree
in degree  . Let
. Let 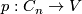 be the projection given by
be the projection given by  and
and 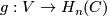 an isomorphism then the map
an isomorphism then the map 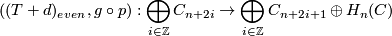
is an isomorphism. Dualizing gives the statement for cohomology.