K-invariant for G/PL (Ex)
From Manifold Atlas
(Difference between revisions)
m |
m |
||
| (2 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | In [[2012 | + | In [[Regensburg Surgery Blockseminar 2012: Program#The surgery exact sequence for TOP and PL|talk 16]] the $2$-local homotopy type of $G/PL$ was described as being |
$$(G/PL)[2]\cong X^4 \times \prod_{n> 1} K(\mathbb{Z},4n)\times K(\mathbb{Z}_2,4n-2)~,$$ | $$(G/PL)[2]\cong X^4 \times \prod_{n> 1} K(\mathbb{Z},4n)\times K(\mathbb{Z}_2,4n-2)~,$$ | ||
where $X^4$ is a two stage Postnikov system with nontrivial homotopy groups | where $X^4$ is a two stage Postnikov system with nontrivial homotopy groups | ||
| Line 15: | Line 15: | ||
{{endthm}} | {{endthm}} | ||
{{beginrem|Hint}} | {{beginrem|Hint}} | ||
| − | Try to construct a degree one normal map $g: | + | Try to construct a degree one normal map $g:\mathbb{C}P^2 \,\sharp \,8 \overline{\mathbb{C}P^2} \to \mathbb{C}P^2$, where $\sharp$ denotes connected sum and $\overline{\mathbb{C}P^2}$ denotes $\mathbb{C}P^2$ with the conjugate complex struture. |
{{endrem}} | {{endrem}} | ||
| − | |||
</wikitex> | </wikitex> | ||
| − | == References == | + | <!-- == References == |
| − | {{#RefList:}} | + | {{#RefList:}} --> |
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises without solution]] | ||
Latest revision as of 20:32, 28 May 2012
In talk 16 the  -local homotopy type of
-local homotopy type of 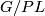 was described as being
was described as being
![\displaystyle (G/PL)[2]\cong X^4 \times \prod_{n> 1} K(\mathbb{Z},4n)\times K(\mathbb{Z}_2,4n-2)~,](/images/math/c/8/6/c862075dfcf3697158c9461040f31393.png)
where 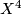 is a two stage Postnikov system with nontrivial homotopy groups
is a two stage Postnikov system with nontrivial homotopy groups
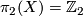 ,
, ![\pi_4(X)=\mathbb{Z}[2]](/images/math/d/9/2/d92ea62f06f90ea2851ae3fcfadebc3f.png) and (non-trivial) Postnikov invariant
and (non-trivial) Postnikov invariant ![k^4\in H^5(K(\mathbb{Z},2),\mathbb{Z}[2])](/images/math/4/3/f/43f59a1ad32290d8cad1218d617f38d2.png) .
The goal of this exercise is to show that
.
The goal of this exercise is to show that 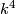 is nonzero.
is nonzero.
Exercise 0.1.
Let 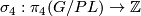 be the surgery obstruction map, and
be the surgery obstruction map, and ![\sigma_4[2]](/images/math/0/9/7/0975f3e335688410198000fe3428564f.png) its
factorization through the localized Hurewicz map
its
factorization through the localized Hurewicz map ![h_{MSO[2]}](/images/math/7/7/f/77f1039224a5ef9080f9af4999b5c2b4.png) , so that
, so that ![\sigma_4=\sigma_4[2]\circ h_{MSO[2]}](/images/math/7/3/c/73cceadfc4d517cc0c3cab942f67c2f9.png) .
Show that if
.
Show that if ![\sigma_4[2]](/images/math/0/9/7/0975f3e335688410198000fe3428564f.png) is surjective, then
is surjective, then 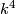 is nonzero.
is nonzero.
Exercise 0.2.
Show that ![\sigma_4[2]](/images/math/0/9/7/0975f3e335688410198000fe3428564f.png) is surjective by constructing a
is surjective by constructing a  -manifold
-manifold 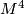 and a map
and a map 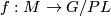 with
surgery invariant 1.
with
surgery invariant 1.
Hint 0.3.
Try to construct a degree one normal map 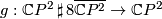 , where
, where  denotes connected sum and
denotes connected sum and 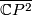 denotes
denotes 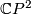 with the conjugate complex struture.
with the conjugate complex struture.