Regensburg Surgery Blockseminar 2012: Program
Each section of this page is devoted to a talk in the Blockseminar.
Please consider using each subsection as a place to build up materials for your talk: e.g. you could post notes or slides, or pictures, or a list of relevant references, or links to related exercises and questions.
[edit] 1 The s-cobordism theorem I
This talk covers [Lück2001, 1.1-1.3].
Start with a clear statement of Theorem 1.1 where the Whitehead group 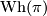 appears as a certain group depending only on
appears as a certain group depending only on 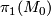 and which is to be defined later. As motivation, quickly state and prove Theorems 1.2 & 1.3.
and which is to be defined later. As motivation, quickly state and prove Theorems 1.2 & 1.3.
Summarise the notation and main results of Section 1.1: these are Definition 1.6, Lemma 1.7, Lemma 1.12, Notation 1.15 and Lemma 1.16.
Review Section 1.2 and then state without proof the Normal Form Lemma 1.24. State and prove Lemmas 1.22 and 1.23.
[edit] 2 The s-cobordism theorem II
This talks covers [Lück2001, 1.3 & 1.4].
Prove Lemma 1.24 and then go through Section 1.4 in detail give the first definition of 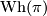 and then state Lemma 1.27. Give the proof of Lemma 1.27 in detail.
and then state Lemma 1.27. Give the proof of Lemma 1.27 in detail.
[edit] 3 The s-cobordism theorem III
This talk covers [Lück2001, Ch.2].
Follow the Introduction and Sections 2.1 and 2.2 closely. State Theorem 2.1 making explicit that (5) is deep. Ensuring that you state and prove Lemma 2.16 and complete the proof of Theorem 1.1 cover as much of 2.1 and 2.2 as time permits.
[edit] 4 Poincaré complexes
This talk covers [Lück2001, 3.1].
Cover the whole section paying particular care with the introduction of homology groups with ![\Zz[\pi]](/images/math/5/9/a/59abcee2c0404c04e89fb508a53c9890.png) -coefficients and local coefficients twisted by the orientation character
-coefficients and local coefficients twisted by the orientation character 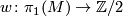 . Give at least one unorientable example.
. Give at least one unorientable example.
[edit] 5 Spherical fibrations and the normal Spivak fibration
This talk covers [Lück2001, 3.2.2 & 3.2.3].
Cover the two subsections in detail: Theorem 3.38 and Lemma 3.40 are the main results. Focus on defining spherical fibrations and clearly stating the main results, then move on to the proofs.
[edit] 6 Normal maps and the Pontrjagin-Thom isomorphism
This talk covers [Lück2001, 3.2.1 & 3.3].
Briefly recall the main results of Section 3.2.1, Theorems 3.26 and 3.28, without proof. Then focus on Section 3.3. The main results are Theorems 3.45 and 3.52.
[edit] 7 Surgery below the middle dimension
This talk covers [Lück2001, 3.4].
Use 3.4.1 mainly as background motivation but do prove Lemma 3.55. Use 3.4.2 as a black box but give more examples of sets of regular homotopy classes of immersions, in particular 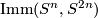 . State and prove Theorems 3.59 and 3.61 in their full glory.
. State and prove Theorems 3.59 and 3.61 in their full glory.
[edit] 8 Intersections and self-intersections
This talk covers [Lück2001, 4.1].
The main results are Lemma 4.3 and 4.7 and Theorem 4.8. Draw lots of pictures. Find and present some examples of immersions with interesting self-intersections.
[edit] 9 Kernels and forms
This talk covers [Lück2001, 4.2].
This is a long talk: the main result is Theorem 4.27.
[edit] 10 Even dimensional surgery obstructions
This talk covers [Lück2001, 4.3 & 4.4].
The main result is Theorem 4.33 and its elaboration, Theorem 4.36, in the simply connected case.
[edit] 11 Odd dimensional surgery obstructions
This talk covers [Lück2001, 4.5 & 4.6].
This is a difficult talk. The main results are Theorems 4.44 and 4.46. It is reasonable to follow Lück but some details are left out. The presenter could also read [Ranicki2002, Section 12].
[edit] 12 Manifolds with boundary and simple surgery obstructions
This talk covers [Lück2001, 4.7].
The main results are Theorems 4.47 and 4.61. You may choose to skip some of the algebraic details related to the simple surgery obstruction.
[edit] 13 The structure set and Wall realisation
This talk covers [Lück2001, 5.1 & 5.2].
The main points are the definition of the structure set and Theorem 5.5.
In addition show that the action of ![L_{n+1}(\Zz[e])](/images/math/d/f/1/df1b9ad5e48e2882ba99f92fa3c225a3.png) on the structure set is via connected sum with homotopy spheres and give a detailed describtion of plumbing: [Browder1972, II 4.10] and then [Browder1972, V 2.1, 2.9 & 2.11]. Note, do not use Browder's definition of the quadratic refinement rather refer to the exercises for the proof of 2.11.
on the structure set is via connected sum with homotopy spheres and give a detailed describtion of plumbing: [Browder1972, II 4.10] and then [Browder1972, V 2.1, 2.9 & 2.11]. Note, do not use Browder's definition of the quadratic refinement rather refer to the exercises for the proof of 2.11.
You may also want to attempt to sketch realisation for odd dimensional  -groups.
-groups.
[edit] 14 The smooth surgery exact sequence
This talk covers [Lück2001, 5.3 & 6.1].
Everything comes together in this talk! The main result is Theorem 5.12. You should also state and prove that the set of diffeomorphisms classes of manifolds homotopy equivalent to a given manifold  is equal to the orbit space
is equal to the orbit space 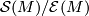 where
where 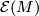 is the group of homotopy automorphisms of
is the group of homotopy automorphisms of  .
.
As an example, begin with the surgery exact sequence for  in Section 6.1.
in Section 6.1.
[edit] 15 Exotic spheres
This talk covers [Lück2001, 6.1-6.5 & 6.7].
There is a good deal of beautiful mathematics to cover in this talk. The main result is Theorem 6.11: quickly make your way to its statement and then explain how computing the various groups and maps in this sequence organises the rest of the talk.
Note that the status of the Kervaire invariant problem has changed since [Lück2001] was written: for the current situation see e.g. Exotic spheres.
[edit] 16 The surgery exact sequence for TOP and PL
This talk covers [Lück2001, 5.4 & 6.6].
The central result if Theorem 5.15. Discuss a little the extra challenges of the new categories: PL is not so hard, TOP is very difficult! Assuming Theorem 5.15 use the surgery exact sequence and the Generalised Poincaré Conjecture to compute the homotopy groups 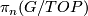 .
.
As an example describe the  surgery exact sequence for
surgery exact sequence for 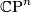 and
and 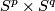 given in [Wall1999, Theorem 14C.2] for
given in [Wall1999, Theorem 14C.2] for 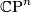 and in [Ranicki1992, Ex. 20.4] and [Kreck&Lück2009, Section 7] for
and in [Ranicki1992, Ex. 20.4] and [Kreck&Lück2009, Section 7] for 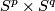 : do not go into details for
: do not go into details for 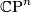 as they will come in the next lecture.
as they will come in the next lecture.
Next state Sullivan's theorems identifying the homotopy type of 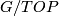 and Kirby-Siebenmann's result on
and Kirby-Siebenmann's result on 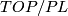 .
.
Take the remainder of the talk to identify the  -local homotopy type of
-local homotopy type of 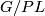 : i.e. give the proof of [Madsen&Milgram1979, Theorem 4.8].
: i.e. give the proof of [Madsen&Milgram1979, Theorem 4.8].
[edit] 17 Manifolds homotopy equivalent to CPn
This talk covers [Wall1999, 14C], [Madsen&Milgram1979, 8C].
State the surgery classification of  -manifolds homotopy equivalent to
-manifolds homotopy equivalent to 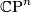 given in [Wall1999, Theorem 14C.2]. In particular emphasise the splitting invariants
given in [Wall1999, Theorem 14C.2]. In particular emphasise the splitting invariants 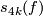 and
and 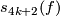 .
.
Then go through [Madsen&Milgram1979, 8C] in detail and in particular prove [Madsen&Milgram1979, Theorem 8.27].
Related material: Fake complex projective spaces
[edit] 18 Fake Tori
This talk covers [Wall1999, 15A].
The ambitious goal of this talks is to prove [Wall1999, Theorem 15A.2].
Present Wall's identification of ![[T^n, G/PL]](/images/math/7/f/3/7f3f6177a9ebb14bf9887b8a64d41a00.png) using the fact that
using the fact that 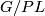 is an infinite loop space. In order to compute
is an infinite loop space. In order to compute 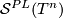 you need to compute the surgery obstruction maps
you need to compute the surgery obstruction maps ![\sigma \colon [T^n, G/PL] \to L_n(\Zz[\Zz^n])](/images/math/c/d/a/cda1eb768e5c10846dbb105dab0a6b31.png) . Assume Wall's calculation of the the
. Assume Wall's calculation of the the  -groups
-groups 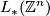 and compute
and compute 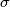 by using splitting obstructions along the sub-tori
by using splitting obstructions along the sub-tori  .
.
[edit] 19 References
- [Browder1972] W. Browder, Surgery on simply-connected manifolds, Springer-Verlag, New York, 1972. MR0358813 (50 #11272) Zbl 0543.57003
- [Kreck&Lück2009] M. Kreck and W. Lück, Topological rigidity for non-aspherical manifolds, Pure Appl. Math. Q. 5 (2009), no.3, Special Issue: In honor of Friedrich Hirzebruch., 873–914. MR2532709 (2010g:57026) Zbl 1196.57018
- [Lück2001] W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Ranicki1992] A. A. Ranicki, Algebraic
 -theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
-theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003