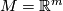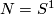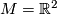Isotopy
Askopenkov (Talk | contribs) (→Ambient and non-ambient isotopy) |
m (→Definition) |
||
| (33 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Authors|Askopenkov}} |
| − | == | + | ==Definition== |
| − | <wikitex>; | + | <wikitex>; |
| + | This page defines isotopies and ambient isotopies between embeddings in either the [[Wikipedia:Differential_manifold#Differentiable_functions|smooth]] (DIFF), [[Wikipedia:Piecewise_linear_function|piecewise-linear]] (PL) or [[Wikipedia:Topological_manifold|topological]] (TOP) categories. These notions usually appear in discussions of details, so a reader is more likely to see in the literature (including Manifold Atlas) isotopy and ambient isotopy as equivalence relations, which are also defined here. By a `CAT embedding' we mean either a `smooth embedding', a `piecewise linear' embedding or a `topological embedding', depending upon the category. By a `CAT homeomorphism' we mean a `diffeomorphism' if CAT=DIFF, a `PL homemomorphism' if CAT=PL or a`homeomorphism' if CAT=TOP. All manifolds are assumed to be compact and $I = [0,1]$ denotes the unit interval. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{beginthm|Definition|(Ambient isotopy)}}\label{dai} | {{beginthm|Definition|(Ambient isotopy)}}\label{dai} | ||
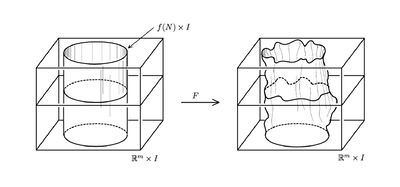
| − | For manifolds $M,N$ two [[Embedding_(simple_definition)|embeddings]] $f,g:N\to M$ | + | For manifolds $M,N$ an [[Wikipedia:Ambient_isotopy|ambient isotopy]] between two CAT [[Embedding_(simple_definition)|embeddings]] $f,g:N\to M$ is a CAT homeomorphism $F:M\times I\to M\times I$ such that |
| − | * $F(y,0)=(y,0)$ for | + | * $F(y,0)=(y,0)$ for all $y\in M,$ |
| − | * $F(f(x),1)=(g(x),1)$ for | + | * $F(f(x),1)=(g(x),1)$ for all $x\in N,$ and |
| − | * $F(M\times\{t\})=M\times\{t\}$ for | + | * $F(M\times\{t\})=M\times\{t\}$ for all $t \in I.$ |
| − | + | [[Image:AmbientIsotopy.jpg|thumb|400px|An ambient isotopy for $M=\Rr^m$: the picture is realistic for $N = S^1$ and $M = \R^2$]] <!--\cite[Figure 1.1]{Skopenkov2006}--> | |
| − | + | Two embeddings $f$ and $g$ are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of $N$ into $M$ (in the smooth category this is non-trivial and proven in \cite[$\S$8, Theorem 1.9]{Hirsch1976}). | |
| − | + | ||
{{endthm}} | {{endthm}} | ||
| − | |||
| − | |||
| − | The [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Introduction|classification of embeddings up to ambient isotopy]] is a classical problem in topology | + | For simple examples of ambient isotopic embeddings and also embeddings which are not ambient isotopic, see \cite[Remark 1.3.a]{Skopenkov2016c}. The [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Introduction|classification of embeddings up to ambient isotopy]] is a classical problem in topology. For an introduction to the case when $N = \R^m$ and also a summary of theorems stating when all embeddings $M \to \R^m$ are isotopic, see \cite{Skopenkov2016c}. |
| + | <!--Ambient isotopy is a stronger equivalence relation than any of the relations non-ambient isotopy, isoposition, concordance, bordism, etc., see below. --> | ||
| − | + | {{beginthm|Remark}} | |
| + | Some authors abbreviate ''ambient isotopy'' to just ''isotopy''. Readers should be careful to clarify the meaning of ''isotopy'' in a particular text. | ||
| + | {{endthm|Remark}} | ||
| − | + | {{beginthm|Definition|(Isotopy)}}\label{di} | |
| − | + | For manifolds $M,N$ two CAT embeddings $f,g:N\to M$ are called ''CAT isotopic'', if there exists an embedding $F:N\times I\to M\times I$ such that | |
| − | + | ||
| − | {{beginthm|Definition|( | + | |
| − | For manifolds $M,N$ two embeddings $f,g:N\to M$ are called '' | + | |
* $F(x,0)=(f(x),0)$, | * $F(x,0)=(f(x),0)$, | ||
| − | * $F(x,1)=(g(x),1)$ for | + | * $F(x,1)=(g(x),1)$ for all $x\in N$ and |
| − | * $F(N\times\{t\})\subset M\times\{t\}$ for | + | * $F(N\times\{t\})\subset M\times\{t\}$ for all $t\in I$. |
| + | Two embeddings $f$ and $g$ are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of $N$ into $M$ (in the smooth category this is non-trivial, see \cite[$\S$8, Theorem 1.9 and Excercise 1]{Hirsch1976}). | ||
{{endthm}} | {{endthm}} | ||
| − | + | {{beginthm|Remark}} | |
| + | In the smooth category ''isotopy'' is also called ''diffeotopy'' by some authors. | ||
| − | + | The set of embeddings of $M$ into $N$ can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of $M$ into $N$ coincides with the path components of the space of embeddings of $M$ into $N$. For details on the space of embeddings and for information in the case of non-compact manifolds see \cite{Geiges2018}. | |
{{endthm}} | {{endthm}} | ||
| − | + | {{beginthm|Theorem}}\label{t:aivsi} In the smooth category, or for $m-n\ge3$ in the PL or TOP category, isotopy implies ambient isotopy \cite[$\S$8.1]{Hirsch1976}, \cite{Hudson&Zeeman1964}, \cite{Hudson1966}, \cite{Akin1969}, \cite{Edwards1975}. | |
| + | {{endthm}} | ||
| − | In the smooth category, ''non-ambient isotopy'' is also called ''diffeotopy''. | + | For $m-n\le2$ this is not so: e.g., any knot $S^1\to\Rr^3$ is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot. |
| − | + | <!--In the smooth category, ''non-ambient isotopy'' is also called ''diffeotopy''.--> | |
| − | + | ||
| − | + | ||
| − | + | ||
{{beginthm|Definition|(Isoposition)}}\label{dipn} | {{beginthm|Definition|(Isoposition)}}\label{dipn} | ||
| Line 62: | Line 46: | ||
For embeddings into $\Rr^m$ PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) \cite[3.22]{Rourke&Sanderson1972}. | For embeddings into $\Rr^m$ PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) \cite[3.22]{Rourke&Sanderson1972}. | ||
It would be interesting to know if the smooth analogue of this result holds. | It would be interesting to know if the smooth analogue of this result holds. | ||
| + | </wikitex> | ||
| + | |||
| + | ==Concordance == | ||
| + | <wikitex>; | ||
{{beginthm|Definition|(Concordance)}}\label{dac} | {{beginthm|Definition|(Concordance)}}\label{dac} | ||
Latest revision as of 04:40, 24 April 2019
|
The user responsible for this page is Askopenkov. No other user may edit this page at present. |
1 Definition
This page defines isotopies and ambient isotopies between embeddings in either the smooth (DIFF), piecewise-linear (PL) or topological (TOP) categories. These notions usually appear in discussions of details, so a reader is more likely to see in the literature (including Manifold Atlas) isotopy and ambient isotopy as equivalence relations, which are also defined here. By a `CAT embedding' we mean either a `smooth embedding', a `piecewise linear' embedding or a `topological embedding', depending upon the category. By a `CAT homeomorphism' we mean a `diffeomorphism' if CAT=DIFF, a `PL homemomorphism' if CAT=PL or a`homeomorphism' if CAT=TOP. All manifolds are assumed to be compact and ![I = [0,1]](/images/math/0/c/8/0c8186b6d2da0ff001e4eb3236a545e0.png) denotes the unit interval.
denotes the unit interval.
Definition 1.1 (Ambient isotopy).
For manifolds 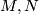 an ambient isotopy between two CAT embeddings
an ambient isotopy between two CAT embeddings 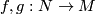 is a CAT homeomorphism
is a CAT homeomorphism 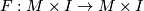 such that
such that
-
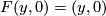 for all
for all 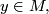
-
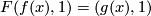 for all
for all 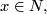 and
and
-
 for all
for all 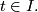
 and
and  are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of
are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of  into
into Tex syntax error(in the smooth category this is non-trivial and proven in [Hirsch1976,
 8, Theorem 1.9]).
8, Theorem 1.9]).
For simple examples of ambient isotopic embeddings and also embeddings which are not ambient isotopic, see [Skopenkov2016c, Remark 1.3.a]. The classification of embeddings up to ambient isotopy is a classical problem in topology. For an introduction to the case when 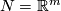 and also a summary of theorems stating when all embeddings
and also a summary of theorems stating when all embeddings 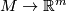 are isotopic, see [Skopenkov2016c].
are isotopic, see [Skopenkov2016c].
Remark 1.2. Some authors abbreviate ambient isotopy to just isotopy. Readers should be careful to clarify the meaning of isotopy in a particular text.
Definition 1.3 (Isotopy).
For manifolds 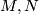 two CAT embeddings
two CAT embeddings 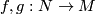 are called CAT isotopic, if there exists an embedding
are called CAT isotopic, if there exists an embedding 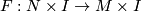 such that
such that
-
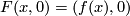 ,
,
-
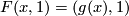 for all
for all 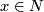 and
and
-
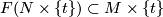 for all
for all 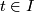 .
.
 and
and  are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of
are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of  into
into Tex syntax error(in the smooth category this is non-trivial, see [Hirsch1976,
 8, Theorem 1.9 and Excercise 1]).
8, Theorem 1.9 and Excercise 1]).
Remark 1.4. In the smooth category isotopy is also called diffeotopy by some authors.
The set of embeddings ofTex syntax errorinto
 can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of
can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of Tex syntax errorinto
 coincides with the path components of the space of embeddings of
coincides with the path components of the space of embeddings of Tex syntax errorinto
 . For details on the space of embeddings and for information in the case of non-compact manifolds see [Geiges2018].
. For details on the space of embeddings and for information in the case of non-compact manifolds see [Geiges2018].
Theorem 1.5. In the smooth category, or for 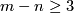 in the PL or TOP category, isotopy implies ambient isotopy [Hirsch1976,
in the PL or TOP category, isotopy implies ambient isotopy [Hirsch1976,  8.1], [Hudson&Zeeman1964], [Hudson1966], [Akin1969], [Edwards1975].
8.1], [Hudson&Zeeman1964], [Hudson1966], [Akin1969], [Edwards1975].
For 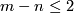 this is not so: e.g., any knot
this is not so: e.g., any knot 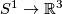 is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot.
is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot.
Definition 1.6 (Isoposition).
For manifolds 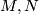 two embeddings
two embeddings 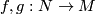 are called (orientation preserving) isopositioned, if there is an (orientation preserving) CAT homeomorphism
are called (orientation preserving) isopositioned, if there is an (orientation preserving) CAT homeomorphism 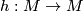 such that
such that 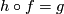 .
.
For embeddings into  PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) [Rourke&Sanderson1972, 3.22].
It would be interesting to know if the smooth analogue of this result holds.
PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) [Rourke&Sanderson1972, 3.22].
It would be interesting to know if the smooth analogue of this result holds.
2 Concordance
Definition 2.1 (Concordance).
For manifolds 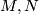 two embeddings
two embeddings 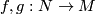 are called ambiently concordant, or just concordant, if there is a homeomorphism onto
are called ambiently concordant, or just concordant, if there is a homeomorphism onto 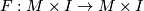 (which is called a concordance) such that
(which is called a concordance) such that
-
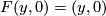 for each
for each 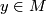 and
and
-
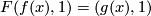 for each
for each 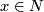 .
.
The definition of non-ambient concordance is analogously obtained from that of non-ambient isotopy by dropping the last condition of level-preservation. Note that in knot theory non-ambient concordance is called cobordism.
In the DIFF category or for 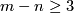 in the PL or TOP category non-ambient concordance implies ambient concordance and ambient isotopy [Lickorish1965], [Hudson1970], [Hudson&Lickorish1971].
(This is not so in the PL or TOP category for codimension 2.) This result allows a reduction of the Knotting Problem to the relativized Embedding Problem, see [Skopenkov2016c,
in the PL or TOP category non-ambient concordance implies ambient concordance and ambient isotopy [Lickorish1965], [Hudson1970], [Hudson&Lickorish1971].
(This is not so in the PL or TOP category for codimension 2.) This result allows a reduction of the Knotting Problem to the relativized Embedding Problem, see [Skopenkov2016c,  1].
1].
3 References
- [Akin1969] E. Akin, Manifold phenomena in the theory of polyhedra, Trans. Amer. Math. Soc. 143 (1969), 413–473. MR0253329 (40 #6544) Zbl 0195.53702
- [Edwards1975] R. D. Edwards, The equivalence of close piecewise linear embeddings, General Topol. Appl. 5 (1975), 147–180. MR0370603 (51 #6830) Zbl 0314.57009
- [Geiges2018] H. Geiges, Isotopies vis-`a-vis level-preserving embeddings, Arch. Math. 110 (2018), 197–200. Available at the arXiv:1708.09703.
- [Hirsch1976] M. W. Hirsch, Differential topology., Graduate Texts in Mathematics, No. 33. Springer-Verlag., New York-Heidelberg, 1976. MR0448362 (56 #6669) Zbl 0356.57001
- [Hudson&Lickorish1971] J. F. P. Hudson and W. B. R. Lickorish, Extending piecewise linear concordances, Quart. J. Math. Oxford Ser. (2) 22 (1971), 1–12. MR0290373 (44 #7557) Zbl 0219.57011
- [Hudson&Zeeman1964] J. F. P. Hudson and E. C. Zeeman, On regular neighbourhoods, Proc. London Math. Soc. (3) 14 (1964), 719–745. MR0166790 (29 #4063) Zbl 0213.25002
- [Hudson1966] J. F. P. Hudson, Extending piecewise-linear isotopies, Proc. London Math. Soc. (3) 16 (1966), 651–668. MR0202147 (34 #2020) Zbl 0141.40802
- [Hudson1970] J. F. P. Hudson, Concordance, isotopy, and diffeotopy, Ann. of Math. (2) 91 (1970), 425–448. MR0259920 (41 #4549) Zbl 0202.54602
- [Lickorish1965] W. B. R. Lickorish, The piecewise linear unknotting of cones, Topology 4 (1965), 67–91. MR0203736 (34 #3585) Zbl 0138.19003
- [Rourke&Sanderson1972] C. Rourke and B. Sanderson, Introduction to piecewise-linear topology., Ergebnisse der Mathematik und ihrer Grenzgebiete. Band 69. Berlin-Heidelberg-New York: Springer-Verlag. VIII, 1972. MR0665919 (83g:57009) Zbl 0254.57010
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
Definition 1.1 (Ambient isotopy).
For manifolds 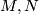 an ambient isotopy between two CAT embeddings
an ambient isotopy between two CAT embeddings 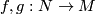 is a CAT homeomorphism
is a CAT homeomorphism 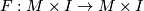 such that
such that
-
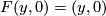 for all
for all 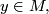
-
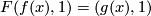 for all
for all 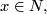 and
and
-
 for all
for all 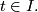
 and
and  are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of
are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of  into
into Tex syntax error(in the smooth category this is non-trivial and proven in [Hirsch1976,
 8, Theorem 1.9]).
8, Theorem 1.9]).
For simple examples of ambient isotopic embeddings and also embeddings which are not ambient isotopic, see [Skopenkov2016c, Remark 1.3.a]. The classification of embeddings up to ambient isotopy is a classical problem in topology. For an introduction to the case when 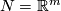 and also a summary of theorems stating when all embeddings
and also a summary of theorems stating when all embeddings 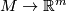 are isotopic, see [Skopenkov2016c].
are isotopic, see [Skopenkov2016c].
Remark 1.2. Some authors abbreviate ambient isotopy to just isotopy. Readers should be careful to clarify the meaning of isotopy in a particular text.
Definition 1.3 (Isotopy).
For manifolds 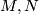 two CAT embeddings
two CAT embeddings 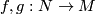 are called CAT isotopic, if there exists an embedding
are called CAT isotopic, if there exists an embedding 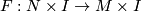 such that
such that
-
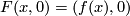 ,
,
-
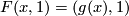 for all
for all 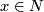 and
and
-
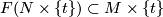 for all
for all 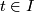 .
.
 and
and  are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of
are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of  into
into Tex syntax error(in the smooth category this is non-trivial, see [Hirsch1976,
 8, Theorem 1.9 and Excercise 1]).
8, Theorem 1.9 and Excercise 1]).
Remark 1.4. In the smooth category isotopy is also called diffeotopy by some authors.
The set of embeddings ofTex syntax errorinto
 can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of
can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of Tex syntax errorinto
 coincides with the path components of the space of embeddings of
coincides with the path components of the space of embeddings of Tex syntax errorinto
 . For details on the space of embeddings and for information in the case of non-compact manifolds see [Geiges2018].
. For details on the space of embeddings and for information in the case of non-compact manifolds see [Geiges2018].
Theorem 1.5. In the smooth category, or for 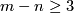 in the PL or TOP category, isotopy implies ambient isotopy [Hirsch1976,
in the PL or TOP category, isotopy implies ambient isotopy [Hirsch1976,  8.1], [Hudson&Zeeman1964], [Hudson1966], [Akin1969], [Edwards1975].
8.1], [Hudson&Zeeman1964], [Hudson1966], [Akin1969], [Edwards1975].
For 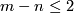 this is not so: e.g., any knot
this is not so: e.g., any knot 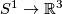 is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot.
is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot.
Definition 1.6 (Isoposition).
For manifolds 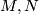 two embeddings
two embeddings 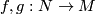 are called (orientation preserving) isopositioned, if there is an (orientation preserving) CAT homeomorphism
are called (orientation preserving) isopositioned, if there is an (orientation preserving) CAT homeomorphism 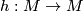 such that
such that 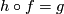 .
.
For embeddings into  PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) [Rourke&Sanderson1972, 3.22].
It would be interesting to know if the smooth analogue of this result holds.
PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) [Rourke&Sanderson1972, 3.22].
It would be interesting to know if the smooth analogue of this result holds.
2 Concordance
Definition 2.1 (Concordance).
For manifolds 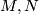 two embeddings
two embeddings 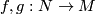 are called ambiently concordant, or just concordant, if there is a homeomorphism onto
are called ambiently concordant, or just concordant, if there is a homeomorphism onto 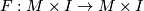 (which is called a concordance) such that
(which is called a concordance) such that
-
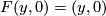 for each
for each 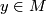 and
and
-
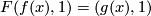 for each
for each 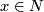 .
.
The definition of non-ambient concordance is analogously obtained from that of non-ambient isotopy by dropping the last condition of level-preservation. Note that in knot theory non-ambient concordance is called cobordism.
In the DIFF category or for 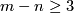 in the PL or TOP category non-ambient concordance implies ambient concordance and ambient isotopy [Lickorish1965], [Hudson1970], [Hudson&Lickorish1971].
(This is not so in the PL or TOP category for codimension 2.) This result allows a reduction of the Knotting Problem to the relativized Embedding Problem, see [Skopenkov2016c,
in the PL or TOP category non-ambient concordance implies ambient concordance and ambient isotopy [Lickorish1965], [Hudson1970], [Hudson&Lickorish1971].
(This is not so in the PL or TOP category for codimension 2.) This result allows a reduction of the Knotting Problem to the relativized Embedding Problem, see [Skopenkov2016c,  1].
1].
3 References
- [Akin1969] E. Akin, Manifold phenomena in the theory of polyhedra, Trans. Amer. Math. Soc. 143 (1969), 413–473. MR0253329 (40 #6544) Zbl 0195.53702
- [Edwards1975] R. D. Edwards, The equivalence of close piecewise linear embeddings, General Topol. Appl. 5 (1975), 147–180. MR0370603 (51 #6830) Zbl 0314.57009
- [Geiges2018] H. Geiges, Isotopies vis-`a-vis level-preserving embeddings, Arch. Math. 110 (2018), 197–200. Available at the arXiv:1708.09703.
- [Hirsch1976] M. W. Hirsch, Differential topology., Graduate Texts in Mathematics, No. 33. Springer-Verlag., New York-Heidelberg, 1976. MR0448362 (56 #6669) Zbl 0356.57001
- [Hudson&Lickorish1971] J. F. P. Hudson and W. B. R. Lickorish, Extending piecewise linear concordances, Quart. J. Math. Oxford Ser. (2) 22 (1971), 1–12. MR0290373 (44 #7557) Zbl 0219.57011
- [Hudson&Zeeman1964] J. F. P. Hudson and E. C. Zeeman, On regular neighbourhoods, Proc. London Math. Soc. (3) 14 (1964), 719–745. MR0166790 (29 #4063) Zbl 0213.25002
- [Hudson1966] J. F. P. Hudson, Extending piecewise-linear isotopies, Proc. London Math. Soc. (3) 16 (1966), 651–668. MR0202147 (34 #2020) Zbl 0141.40802
- [Hudson1970] J. F. P. Hudson, Concordance, isotopy, and diffeotopy, Ann. of Math. (2) 91 (1970), 425–448. MR0259920 (41 #4549) Zbl 0202.54602
- [Lickorish1965] W. B. R. Lickorish, The piecewise linear unknotting of cones, Topology 4 (1965), 67–91. MR0203736 (34 #3585) Zbl 0138.19003
- [Rourke&Sanderson1972] C. Rourke and B. Sanderson, Introduction to piecewise-linear topology., Ergebnisse der Mathematik und ihrer Grenzgebiete. Band 69. Berlin-Heidelberg-New York: Springer-Verlag. VIII, 1972. MR0665919 (83g:57009) Zbl 0254.57010
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
Definition 1.1 (Ambient isotopy).
For manifolds 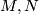 an ambient isotopy between two CAT embeddings
an ambient isotopy between two CAT embeddings 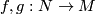 is a CAT homeomorphism
is a CAT homeomorphism 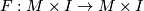 such that
such that
-
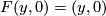 for all
for all 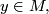
-
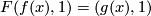 for all
for all 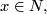 and
and
-
 for all
for all 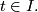
 and
and  are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of
are called ambient isotopic if there is an ambient isotopy between them. Ambient isotopy defines an equivalence relation on the set of CAT embeddings of  into
into Tex syntax error(in the smooth category this is non-trivial and proven in [Hirsch1976,
 8, Theorem 1.9]).
8, Theorem 1.9]).
For simple examples of ambient isotopic embeddings and also embeddings which are not ambient isotopic, see [Skopenkov2016c, Remark 1.3.a]. The classification of embeddings up to ambient isotopy is a classical problem in topology. For an introduction to the case when 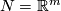 and also a summary of theorems stating when all embeddings
and also a summary of theorems stating when all embeddings 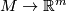 are isotopic, see [Skopenkov2016c].
are isotopic, see [Skopenkov2016c].
Remark 1.2. Some authors abbreviate ambient isotopy to just isotopy. Readers should be careful to clarify the meaning of isotopy in a particular text.
Definition 1.3 (Isotopy).
For manifolds 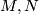 two CAT embeddings
two CAT embeddings 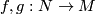 are called CAT isotopic, if there exists an embedding
are called CAT isotopic, if there exists an embedding 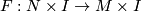 such that
such that
-
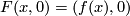 ,
,
-
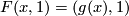 for all
for all 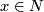 and
and
-
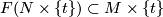 for all
for all 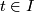 .
.
 and
and  are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of
are called isotopic if there is an isotopy between them. Isotopy defines an equivalence relation on the set of embeddings of  into
into Tex syntax error(in the smooth category this is non-trivial, see [Hirsch1976,
 8, Theorem 1.9 and Excercise 1]).
8, Theorem 1.9 and Excercise 1]).
Remark 1.4. In the smooth category isotopy is also called diffeotopy by some authors.
The set of embeddings ofTex syntax errorinto
 can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of
can be topologised in such a way that an isotopy is equivalent to a continuous path of embeddings. In this case the set of isotopy classes of embeddings of Tex syntax errorinto
 coincides with the path components of the space of embeddings of
coincides with the path components of the space of embeddings of Tex syntax errorinto
 . For details on the space of embeddings and for information in the case of non-compact manifolds see [Geiges2018].
. For details on the space of embeddings and for information in the case of non-compact manifolds see [Geiges2018].
Theorem 1.5. In the smooth category, or for 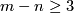 in the PL or TOP category, isotopy implies ambient isotopy [Hirsch1976,
in the PL or TOP category, isotopy implies ambient isotopy [Hirsch1976,  8.1], [Hudson&Zeeman1964], [Hudson1966], [Akin1969], [Edwards1975].
8.1], [Hudson&Zeeman1964], [Hudson1966], [Akin1969], [Edwards1975].
For 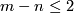 this is not so: e.g., any knot
this is not so: e.g., any knot 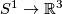 is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot.
is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unkot.
Definition 1.6 (Isoposition).
For manifolds 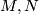 two embeddings
two embeddings 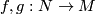 are called (orientation preserving) isopositioned, if there is an (orientation preserving) CAT homeomorphism
are called (orientation preserving) isopositioned, if there is an (orientation preserving) CAT homeomorphism 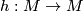 such that
such that 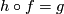 .
.
For embeddings into  PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) [Rourke&Sanderson1972, 3.22].
It would be interesting to know if the smooth analogue of this result holds.
PL orientation preserving isoposition is equivalent to PL isotopy (the Alexander-Guggenheim Theorem) [Rourke&Sanderson1972, 3.22].
It would be interesting to know if the smooth analogue of this result holds.
2 Concordance
Definition 2.1 (Concordance).
For manifolds 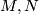 two embeddings
two embeddings 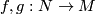 are called ambiently concordant, or just concordant, if there is a homeomorphism onto
are called ambiently concordant, or just concordant, if there is a homeomorphism onto 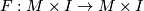 (which is called a concordance) such that
(which is called a concordance) such that
-
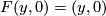 for each
for each 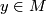 and
and
-
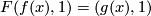 for each
for each 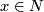 .
.
The definition of non-ambient concordance is analogously obtained from that of non-ambient isotopy by dropping the last condition of level-preservation. Note that in knot theory non-ambient concordance is called cobordism.
In the DIFF category or for 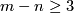 in the PL or TOP category non-ambient concordance implies ambient concordance and ambient isotopy [Lickorish1965], [Hudson1970], [Hudson&Lickorish1971].
(This is not so in the PL or TOP category for codimension 2.) This result allows a reduction of the Knotting Problem to the relativized Embedding Problem, see [Skopenkov2016c,
in the PL or TOP category non-ambient concordance implies ambient concordance and ambient isotopy [Lickorish1965], [Hudson1970], [Hudson&Lickorish1971].
(This is not so in the PL or TOP category for codimension 2.) This result allows a reduction of the Knotting Problem to the relativized Embedding Problem, see [Skopenkov2016c,  1].
1].
3 References
- [Akin1969] E. Akin, Manifold phenomena in the theory of polyhedra, Trans. Amer. Math. Soc. 143 (1969), 413–473. MR0253329 (40 #6544) Zbl 0195.53702
- [Edwards1975] R. D. Edwards, The equivalence of close piecewise linear embeddings, General Topol. Appl. 5 (1975), 147–180. MR0370603 (51 #6830) Zbl 0314.57009
- [Geiges2018] H. Geiges, Isotopies vis-`a-vis level-preserving embeddings, Arch. Math. 110 (2018), 197–200. Available at the arXiv:1708.09703.
- [Hirsch1976] M. W. Hirsch, Differential topology., Graduate Texts in Mathematics, No. 33. Springer-Verlag., New York-Heidelberg, 1976. MR0448362 (56 #6669) Zbl 0356.57001
- [Hudson&Lickorish1971] J. F. P. Hudson and W. B. R. Lickorish, Extending piecewise linear concordances, Quart. J. Math. Oxford Ser. (2) 22 (1971), 1–12. MR0290373 (44 #7557) Zbl 0219.57011
- [Hudson&Zeeman1964] J. F. P. Hudson and E. C. Zeeman, On regular neighbourhoods, Proc. London Math. Soc. (3) 14 (1964), 719–745. MR0166790 (29 #4063) Zbl 0213.25002
- [Hudson1966] J. F. P. Hudson, Extending piecewise-linear isotopies, Proc. London Math. Soc. (3) 16 (1966), 651–668. MR0202147 (34 #2020) Zbl 0141.40802
- [Hudson1970] J. F. P. Hudson, Concordance, isotopy, and diffeotopy, Ann. of Math. (2) 91 (1970), 425–448. MR0259920 (41 #4549) Zbl 0202.54602
- [Lickorish1965] W. B. R. Lickorish, The piecewise linear unknotting of cones, Topology 4 (1965), 67–91. MR0203736 (34 #3585) Zbl 0138.19003
- [Rourke&Sanderson1972] C. Rourke and B. Sanderson, Introduction to piecewise-linear topology., Ergebnisse der Mathematik und ihrer Grenzgebiete. Band 69. Berlin-Heidelberg-New York: Springer-Verlag. VIII, 1972. MR0665919 (83g:57009) Zbl 0254.57010
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.