Embedding (simple definition)
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Definition
A smooth embedding of a smooth compact manifold  into a smooth manifold is a smooth injective map
into a smooth manifold is a smooth injective map 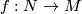 such that
such that
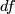 is a monomorphism at each point.
(See an equivalent alternative definition which works for non-compact manifolds and involves immersions.
A smooth immersion is a smooth map
is a monomorphism at each point.
(See an equivalent alternative definition which works for non-compact manifolds and involves immersions.
A smooth immersion is a smooth map 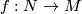 such that
such that 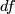 is a monomorphism at each point.
See an equivalent alternative definition.)
is a monomorphism at each point.
See an equivalent alternative definition.)
A map  of a polyhedron
of a polyhedron  is piecewise-linear (PL) if it is linear on each simplex of some smooth triangulation of
is piecewise-linear (PL) if it is linear on each simplex of some smooth triangulation of  .
A PL embedding of a compact polyhedron
.
A PL embedding of a compact polyhedron  into
into  is a PL injective map
is a PL injective map  .
.
A topological embedding of a compact subset 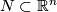 into
into  is a continuous injective map
is a continuous injective map  .
.
Classification of embeddings up to isotopy is a classical problem in topology, see [Skopenkov2016c].
[edit] 2 References
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.