Homology braid II (Ex)
(Difference between revisions)
(Created page with "<wikitex>; Let $M$ be a closed $n$-dimensional manifold and $g:S^k\times D^{n-k}\hookrightarrow M$ a framed embedding. Denote by $M'$ the effect of a surgery on $M$ and by $W$...") |
m |
||
| Line 9: | Line 9: | ||
Denote by $\omega$ the orientation character of $M$, i.e. $\omega:\pi=\pi_1(M)\rightarrow \mathbb{Z}_2$ and by $\widetilde{W},\widetilde{M},\widetilde{M}'$ the corresponding universal covers. Write $H_i(\widetilde{M})$ etc. for the homology with $\mathbb{Z}[\pi]$-coefficients. | Denote by $\omega$ the orientation character of $M$, i.e. $\omega:\pi=\pi_1(M)\rightarrow \mathbb{Z}_2$ and by $\widetilde{W},\widetilde{M},\widetilde{M}'$ the corresponding universal covers. Write $H_i(\widetilde{M})$ etc. for the homology with $\mathbb{Z}[\pi]$-coefficients. | ||
| − | + | '''1)''' Show that there exists a commutative braid of exact sequences | |
$$ | $$ | ||
| − | + | \def\curv{1.5pc}% Adjust the curvature of the curved arrows here | |
\xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here | \xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here | ||
H_{i+1}(\widetilde{W},\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{W},\widetilde{M}') \\ | H_{i+1}(\widetilde{W},\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{W},\widetilde{M}') \\ | ||
| Line 19: | Line 19: | ||
} | } | ||
$$ | $$ | ||
| − | + | ||
| + | '''2)''' Show that the relative homology modules are given by | ||
$$ | $$ | ||
H_{i}(\widetilde{W},\widetilde{M})=\left\{\begin{array}{ll} \mathbb{Z}[\pi] & \textrm{if } i=k+1\\ | H_{i}(\widetilde{W},\widetilde{M})=\left\{\begin{array}{ll} \mathbb{Z}[\pi] & \textrm{if } i=k+1\\ | ||
| Line 30: | Line 31: | ||
\end{array}\right. | \end{array}\right. | ||
$$ | $$ | ||
| − | + | '''3)'''Assume $n=2k$ and look at the top bit of the braid | |
$$ | $$ | ||
\def\curv{1.5pc}% Adjust the curvature of the curved arrows here | \def\curv{1.5pc}% Adjust the curvature of the curved arrows here | ||
| Line 37: | Line 38: | ||
} | } | ||
$$ | $$ | ||
| − | Let $x$ be the Hurewicz image of $[g|]$ with $g|:S^{k}\times 0\hookrightarrow M$ being the restriction of the framed embedding we do the surgery on. | + | Let $x$ be the Hurewicz image of $[g|]$ with $g|:S^{k}\times 0\hookrightarrow M$ being the restriction of the framed embedding we do the surgery on. |
| − | a)Verify that $\alpha$ is (geometrically) given by sending the generator 1 to $x$. | + | |
| − | b)Verify that $\beta$ is (geometrically) given by sending a class $y$ to its (equivariant) homology intersection with $x$, $\lambda(x,y)\in\mathbb{Z}[\pi]$. | + | '''a)''' Verify that $\alpha$ is (geometrically) given by sending the generator 1 to $x$. |
| + | |||
| + | '''b)''' Verify that $\beta$ is (geometrically) given by sending a class $y$ to its (equivariant) homology intersection with $x$, $\lambda(x,y)\in\mathbb{Z}[\pi]$. | ||
Revision as of 23:08, 15 March 2012
Let  be a closed
be a closed  -dimensional manifold and
-dimensional manifold and 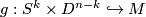 a framed embedding. Denote by
a framed embedding. Denote by 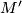 the effect of a surgery on
the effect of a surgery on  and by
and by  the corresponding trace, i.e.
the corresponding trace, i.e.
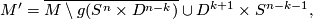
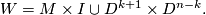
Denote by  the orientation character of
the orientation character of  , i.e.
, i.e. 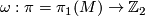 and by
and by 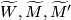 the corresponding universal covers. Write
the corresponding universal covers. Write 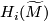 etc. for the homology with
etc. for the homology with ![\mathbb{Z}[\pi]](/images/math/5/3/9/5393263cfc1a4eb9ce95b62982af4354.png) -coefficients.
-coefficients.
1) Show that there exists a commutative braid of exact sequences
![\displaystyle \def\curv{1.5pc}% Adjust the curvature of the curved arrows here \xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here H_{i+1}(\widetilde{W},\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{W},\widetilde{M}') \\ & H_{i+1}(\widetilde{W},\widetilde{M}\cup\widetilde{M}') \ar[dr] \ar[ur] && H_{i}(\widetilde{W}) \ar[dr] \ar[ur] \\ H_{i+1}(\widetilde{W},\widetilde{M}') \ar[ur] \ar@/d\curv/[rr] && H_{i}(\widetilde{M}') \ar[ur] \ar@/d\curv/[rr] && H_{i}(\widetilde{W},\widetilde{M}) }](/images/math/0/a/c/0ac9ff3212a207c04f3a508a8ca3d33b.png)
2) Show that the relative homology modules are given by
![\displaystyle H_{i}(\widetilde{W},\widetilde{M})=\left\{\begin{array}{ll} \mathbb{Z}[\pi] & \textrm{if } i=k+1\\ 0 & \textrm{otherwise}\\ \end{array}\right.](/images/math/e/8/d/e8d19e3beaabd10875a353c3e092aa59.png)
![\displaystyle H_{i}(\widetilde{W},\widetilde{M}')=\left\{\begin{array}{ll} \mathbb{Z}[\pi] & \textrm{if } i=n-k\\ 0 & \textrm{otherwise}\\ \end{array}\right.](/images/math/4/e/9/4e94c69a1a666a2a0ca4ccabfb9874f9.png)
3)Assume 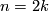 and look at the top bit of the braid
and look at the top bit of the braid
![\displaystyle \def\curv{1.5pc}% Adjust the curvature of the curved arrows here \xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here H_{k+1}(\widetilde{W},\widetilde{M}) \ar@/u\curv/[rr]^{\alpha} && H_{k}(\widetilde{M}) \ar@/u\curv/[rr]^{\beta} && H_{k}(\widetilde{W},\widetilde{M}') }](/images/math/2/7/5/275314403ddad07c18535bfb6e0827bf.png)
Let  be the Hurewicz image of
be the Hurewicz image of ![[g|]](/images/math/d/1/f/d1f9a93e2e2c0f0312d1e41594be235a.png) with
with 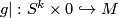 being the restriction of the framed embedding we do the surgery on.
being the restriction of the framed embedding we do the surgery on.
a) Verify that  is (geometrically) given by sending the generator 1 to
is (geometrically) given by sending the generator 1 to  .
.
b) Verify that  is (geometrically) given by sending a class
is (geometrically) given by sending a class  to its (equivariant) homology intersection with
to its (equivariant) homology intersection with  ,
, ![\lambda(x,y)\in\mathbb{Z}[\pi]](/images/math/1/c/3/1c30f65fde26493de4f98dd72befc3af.png) .
.