Fundamental groups of 3-dimensional spherical space forms
|
The user responsible for this page is Wpolitarczyk. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
The purpose of this article is to describe fundamental groups of  -dimensional spherical space forms. For the historical context refer to this article. Today we know the whole list of groups which arise as fundamental groups of
-dimensional spherical space forms. For the historical context refer to this article. Today we know the whole list of groups which arise as fundamental groups of  -dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in
-dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in  . In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on
. In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on  . All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by
. All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by 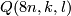 . Question whether these groups act on
. Question whether these groups act on  remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
2 Finite subgroups of SO(4)
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
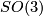 ,
,
- use the covering map
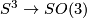 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 is doubly covered by
is doubly covered by 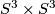 to determine its finite groups.
to determine its finite groups.
2.1 Finite subgroups of SO(3)
To classify finite subgroups of 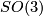 one has to analyse action of these groups on
one has to analyse action of these groups on  . From Riemann-Hurwitz formula we obtain the following equation
. From Riemann-Hurwitz formula we obtain the following equation
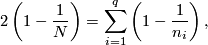
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 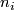 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of 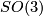 is either
is either
These groups are called polyhedral groups.
2.2 Finite subgroups of S^3
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
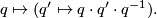
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 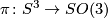 with kernel equal to
with kernel equal to 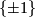 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 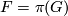 . If
. If 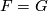 , then, since
, then, since 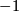 is the only element of
is the only element of  of order
of order  ,
,  and
and  must be both of odd order. Therefore comparing this with the list of finite subgroups of
must be both of odd order. Therefore comparing this with the list of finite subgroups of 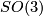 yields that
yields that  and
and  are both cyclic of odd order. On the other hand, if
are both cyclic of odd order. On the other hand, if 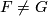 , then
, then  is an extension of the form
is an extension of the form
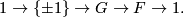
These considerations yields the following theorem.
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either
is either
- cyclic group,
- binary dihedral group,
- binary tetrahedral group,
- binary octahedral group or
- binary icosahedralhedral group.
These groups are called binary polyhedral groups.
2.3 Finite subgroups of SO(4)
To perform the final step, consider a homomophism
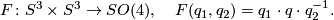
Its kernel is equal to 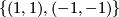 .
.
Finite subgroups of 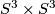 can be determined by Goursat's lemma. This lemma says, that every finite subgroup of
can be determined by Goursat's lemma. This lemma says, that every finite subgroup of 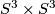 is isomorphic to the fibre product
is isomorphic to the fibre product 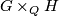 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 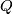 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of SO(4)
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 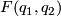 to be fixed point free for
to be fixed point free for 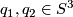 .
.
Lemma 2.3 [Wolf2011].
Let 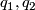 be unit quaternions, then
be unit quaternions, then 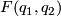 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 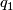 is conjgate to
is conjgate to 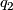 in
in  .
.
Proof. This is a simple observation

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
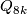 ,
,
- binary tetrahedral group
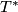 ,
,
- binary icosahedral group
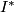 ,
,
- groups
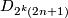 , for
, for 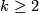 and
and 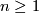 , with presentation
, with presentation
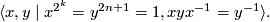
- groups
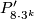 defined by the following presentation
defined by the following presentation
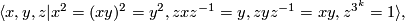
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
In [Milnor1957] author proves the following theorem.
Theorem 3.1.
If  is a finite group which admits a fixed-point free action on a sphere
is a finite group which admits a fixed-point free action on a sphere 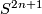 , then for every prime
, then for every prime  every subgroup of
every subgroup of  of order
of order 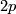 is cyclic.
is cyclic.
This theorem allowed him to choose all possible candidates, from the list compiled by Zassenhaus and Suzuki of groups with periodic cohomology, which could possibly act on  . Apart from groups which admit a fixed point free representation in
. Apart from groups which admit a fixed point free representation in  he obtained the following family of groups.
he obtained the following family of groups.
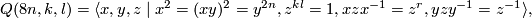
where 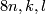 are relatively prime integers and
are relatively prime integers and
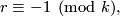
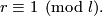
Groups 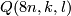 were excluded from the list of fundamental groups of
were excluded from the list of fundamental groups of  -manifolds only after resolution of the Geometrization Conjecture.
-manifolds only after resolution of the Geometrization Conjecture.
4 References
- [Milnor1957] J. Milnor, Groups which act on
 without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219
 -dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in
-dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in  . In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on
. In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on  . All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by
. All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by 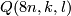 . Question whether these groups act on
. Question whether these groups act on  remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
2 Finite subgroups of SO(4)
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
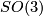 ,
,
- use the covering map
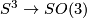 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 is doubly covered by
is doubly covered by 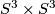 to determine its finite groups.
to determine its finite groups.
2.1 Finite subgroups of SO(3)
To classify finite subgroups of 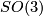 one has to analyse action of these groups on
one has to analyse action of these groups on  . From Riemann-Hurwitz formula we obtain the following equation
. From Riemann-Hurwitz formula we obtain the following equation
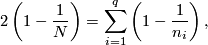
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 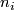 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of 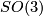 is either
is either
These groups are called polyhedral groups.
2.2 Finite subgroups of S^3
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
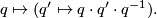
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 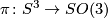 with kernel equal to
with kernel equal to 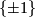 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 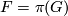 . If
. If 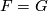 , then, since
, then, since 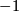 is the only element of
is the only element of  of order
of order  ,
,  and
and  must be both of odd order. Therefore comparing this with the list of finite subgroups of
must be both of odd order. Therefore comparing this with the list of finite subgroups of 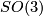 yields that
yields that  and
and  are both cyclic of odd order. On the other hand, if
are both cyclic of odd order. On the other hand, if 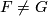 , then
, then  is an extension of the form
is an extension of the form
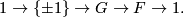
These considerations yields the following theorem.
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either
is either
- cyclic group,
- binary dihedral group,
- binary tetrahedral group,
- binary octahedral group or
- binary icosahedralhedral group.
These groups are called binary polyhedral groups.
2.3 Finite subgroups of SO(4)
To perform the final step, consider a homomophism
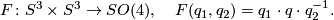
Its kernel is equal to 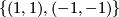 .
.
Finite subgroups of 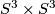 can be determined by Goursat's lemma. This lemma says, that every finite subgroup of
can be determined by Goursat's lemma. This lemma says, that every finite subgroup of 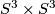 is isomorphic to the fibre product
is isomorphic to the fibre product 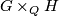 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 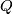 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of SO(4)
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 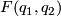 to be fixed point free for
to be fixed point free for 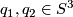 .
.
Lemma 2.3 [Wolf2011].
Let 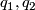 be unit quaternions, then
be unit quaternions, then 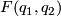 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 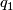 is conjgate to
is conjgate to 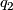 in
in  .
.
Proof. This is a simple observation
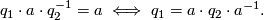

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
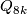 ,
,
- binary tetrahedral group
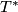 ,
,
- binary icosahedral group
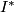 ,
,
- groups
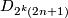 , for
, for 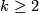 and
and 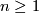 , with presentation
, with presentation
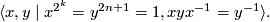
- groups
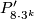 defined by the following presentation
defined by the following presentation
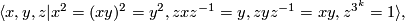
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
In [Milnor1957] author proves the following theorem.
Theorem 3.1.
If  is a finite group which admits a fixed-point free action on a sphere
is a finite group which admits a fixed-point free action on a sphere 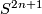 , then for every prime
, then for every prime  every subgroup of
every subgroup of  of order
of order 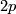 is cyclic.
is cyclic.
This theorem allowed him to choose all possible candidates, from the list compiled by Zassenhaus and Suzuki of groups with periodic cohomology, which could possibly act on  . Apart from groups which admit a fixed point free representation in
. Apart from groups which admit a fixed point free representation in  he obtained the following family of groups.
he obtained the following family of groups.
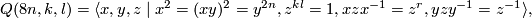
where 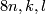 are relatively prime integers and
are relatively prime integers and
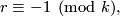
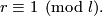
Groups 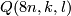 were excluded from the list of fundamental groups of
were excluded from the list of fundamental groups of  -manifolds only after resolution of the Geometrization Conjecture.
-manifolds only after resolution of the Geometrization Conjecture.
4 References
- [Milnor1957] J. Milnor, Groups which act on
 without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219
 -dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in
-dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in  . In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on
. In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on  . All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by
. All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by 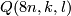 . Question whether these groups act on
. Question whether these groups act on  remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
2 Finite subgroups of SO(4)
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
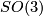 ,
,
- use the covering map
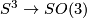 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 is doubly covered by
is doubly covered by 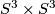 to determine its finite groups.
to determine its finite groups.
2.1 Finite subgroups of SO(3)
To classify finite subgroups of 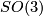 one has to analyse action of these groups on
one has to analyse action of these groups on  . From Riemann-Hurwitz formula we obtain the following equation
. From Riemann-Hurwitz formula we obtain the following equation
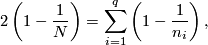
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 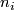 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of 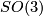 is either
is either
These groups are called polyhedral groups.
2.2 Finite subgroups of S^3
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
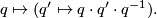
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 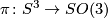 with kernel equal to
with kernel equal to 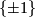 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 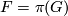 . If
. If 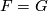 , then, since
, then, since 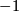 is the only element of
is the only element of  of order
of order  ,
,  and
and  must be both of odd order. Therefore comparing this with the list of finite subgroups of
must be both of odd order. Therefore comparing this with the list of finite subgroups of 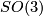 yields that
yields that  and
and  are both cyclic of odd order. On the other hand, if
are both cyclic of odd order. On the other hand, if 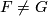 , then
, then  is an extension of the form
is an extension of the form
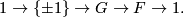
These considerations yields the following theorem.
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either
is either
- cyclic group,
- binary dihedral group,
- binary tetrahedral group,
- binary octahedral group or
- binary icosahedralhedral group.
These groups are called binary polyhedral groups.
2.3 Finite subgroups of SO(4)
To perform the final step, consider a homomophism
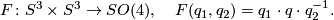
Its kernel is equal to 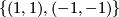 .
.
Finite subgroups of 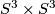 can be determined by Goursat's lemma. This lemma says, that every finite subgroup of
can be determined by Goursat's lemma. This lemma says, that every finite subgroup of 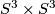 is isomorphic to the fibre product
is isomorphic to the fibre product 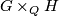 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 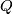 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of SO(4)
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 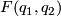 to be fixed point free for
to be fixed point free for 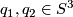 .
.
Lemma 2.3 [Wolf2011].
Let 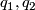 be unit quaternions, then
be unit quaternions, then 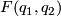 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 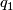 is conjgate to
is conjgate to 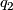 in
in  .
.
Proof. This is a simple observation
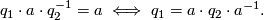

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
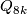 ,
,
- binary tetrahedral group
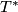 ,
,
- binary icosahedral group
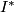 ,
,
- groups
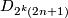 , for
, for 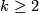 and
and 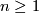 , with presentation
, with presentation
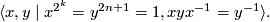
- groups
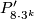 defined by the following presentation
defined by the following presentation
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
In [Milnor1957] author proves the following theorem.
Theorem 3.1.
If  is a finite group which admits a fixed-point free action on a sphere
is a finite group which admits a fixed-point free action on a sphere 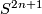 , then for every prime
, then for every prime  every subgroup of
every subgroup of  of order
of order 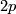 is cyclic.
is cyclic.
This theorem allowed him to choose all possible candidates, from the list compiled by Zassenhaus and Suzuki of groups with periodic cohomology, which could possibly act on  . Apart from groups which admit a fixed point free representation in
. Apart from groups which admit a fixed point free representation in  he obtained the following family of groups.
he obtained the following family of groups.
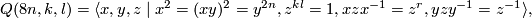
where 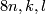 are relatively prime integers and
are relatively prime integers and
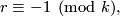
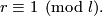
Groups 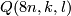 were excluded from the list of fundamental groups of
were excluded from the list of fundamental groups of  -manifolds only after resolution of the Geometrization Conjecture.
-manifolds only after resolution of the Geometrization Conjecture.
4 References
- [Milnor1957] J. Milnor, Groups which act on
 without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219
 -dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in
-dimensional spherical space forms. These are exactly groups which admit a fixed-point free representation in  . In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on
. In 1950's Milnor in [Milnor1957] provided a list of all finite groups which could possibly act freely but not necessarilly linearly on  . All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by
. All groups mentioned earlier belong to this list however there was also included a family of finite groups denoted by 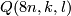 . Question whether these groups act on
. Question whether these groups act on  remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition of the first part is based on [Wolf2011].
2 Finite subgroups of SO(4)
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
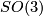 ,
,
- use the covering map
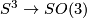 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 is doubly covered by
is doubly covered by 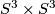 to determine its finite groups.
to determine its finite groups.
2.1 Finite subgroups of SO(3)
To classify finite subgroups of 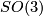 one has to analyse action of these groups on
one has to analyse action of these groups on  . From Riemann-Hurwitz formula we obtain the following equation
. From Riemann-Hurwitz formula we obtain the following equation
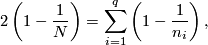
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 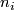 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of 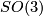 is either
is either
These groups are called polyhedral groups.
2.2 Finite subgroups of S^3
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
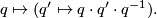
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 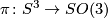 with kernel equal to
with kernel equal to 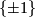 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 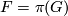 . If
. If 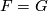 , then, since
, then, since 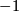 is the only element of
is the only element of  of order
of order  ,
,  and
and  must be both of odd order. Therefore comparing this with the list of finite subgroups of
must be both of odd order. Therefore comparing this with the list of finite subgroups of 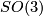 yields that
yields that  and
and  are both cyclic of odd order. On the other hand, if
are both cyclic of odd order. On the other hand, if 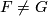 , then
, then  is an extension of the form
is an extension of the form
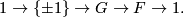
These considerations yields the following theorem.
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either
is either
- cyclic group,
- binary dihedral group,
- binary tetrahedral group,
- binary octahedral group or
- binary icosahedralhedral group.
These groups are called binary polyhedral groups.
2.3 Finite subgroups of SO(4)
To perform the final step, consider a homomophism
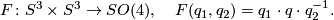
Its kernel is equal to 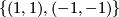 .
.
Finite subgroups of 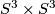 can be determined by Goursat's lemma. This lemma says, that every finite subgroup of
can be determined by Goursat's lemma. This lemma says, that every finite subgroup of 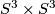 is isomorphic to the fibre product
is isomorphic to the fibre product 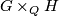 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 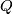 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of SO(4)
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 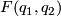 to be fixed point free for
to be fixed point free for 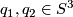 .
.
Lemma 2.3 [Wolf2011].
Let 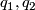 be unit quaternions, then
be unit quaternions, then 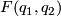 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 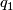 is conjgate to
is conjgate to 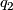 in
in  .
.
Proof. This is a simple observation
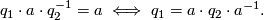

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
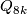 ,
,
- binary tetrahedral group
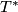 ,
,
- binary icosahedral group
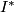 ,
,
- groups
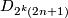 , for
, for 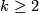 and
and 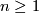 , with presentation
, with presentation
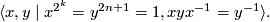
- groups
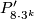 defined by the following presentation
defined by the following presentation
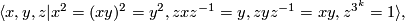
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
In [Milnor1957] author proves the following theorem.
Theorem 3.1.
If  is a finite group which admits a fixed-point free action on a sphere
is a finite group which admits a fixed-point free action on a sphere 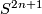 , then for every prime
, then for every prime  every subgroup of
every subgroup of  of order
of order 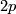 is cyclic.
is cyclic.
This theorem allowed him to choose all possible candidates, from the list compiled by Zassenhaus and Suzuki of groups with periodic cohomology, which could possibly act on  . Apart from groups which admit a fixed point free representation in
. Apart from groups which admit a fixed point free representation in  he obtained the following family of groups.
he obtained the following family of groups.
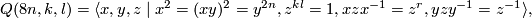
where 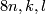 are relatively prime integers and
are relatively prime integers and
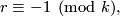
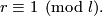
Groups 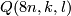 were excluded from the list of fundamental groups of
were excluded from the list of fundamental groups of  -manifolds only after resolution of the Geometrization Conjecture.
-manifolds only after resolution of the Geometrization Conjecture.
4 References
- [Milnor1957] J. Milnor, Groups which act on
 without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219