Fundamental groups of 3-dimensional spherical space forms
|
The user responsible for this page is Wpolitarczyk. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
The purpose of this article is to describe fundamental groups of  -dimensional spherical space forms. For the historical context refer to this article. Today the list of groups which arise as fundamental groups of
-dimensional spherical space forms. For the historical context refer to this article. Today the list of groups which arise as fundamental groups of  -dimensional spherical space forms is known. These are exactly the groups which admit a fixed-point free representation in
-dimensional spherical space forms is known. These are exactly the groups which admit a fixed-point free representation in  . In 1950's Milnor in [Milnor1957] compiled a list of all finite groups which could possibly act freely but not necessarily linearly on
. In 1950's Milnor in [Milnor1957] compiled a list of all finite groups which could possibly act freely but not necessarily linearly on  . Apart from the groups admitting fixed-point free representations in
. Apart from the groups admitting fixed-point free representations in  , Milnor's list also included a family of finite groups denoted by
, Milnor's list also included a family of finite groups denoted by 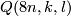 (see Theorem 3.1 below for their definition). The problem whether these groups can act on
(see Theorem 3.1 below for their definition). The problem whether these groups can act on  remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition in this article is based on Chapter 7.5 of [Wolf2011], which surveys results of Hopf [Hopf1926] and Seifert-Threlfall [Threlfall&Seifert1931], [Threlfall&Seifert1933].
remained unsolved until the proof of the Geometrization Conjecture was finished by Perelman. The exposition in this article is based on Chapter 7.5 of [Wolf2011], which surveys results of Hopf [Hopf1926] and Seifert-Threlfall [Threlfall&Seifert1931], [Threlfall&Seifert1933].
2 Finite subgroups of SO(4)
The list of finite subgroups of  can be determined in three steps:
can be determined in three steps:
- determine finite subgroups of
 ,
,
- use the covering map
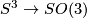 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 is doubly covered by
is doubly covered by 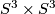 to determine its finite groups.
to determine its finite groups.
2.1 Finite subgroups of SO(3)
To classify finite subgroups of  , we have to analyze the action of these groups on
, we have to analyze the action of these groups on  .
From Riemann-Hurwitz formula we obtain the following equation
.
From Riemann-Hurwitz formula we obtain the following equation
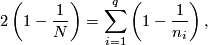
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy groups, and
denotes number of orbits with non-trivial isotropy groups, and 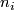 denotes the order of the respective isotropy group.
Solutions to this equation yield the desired list of finite subgroups of
denotes the order of the respective isotropy group.
Solutions to this equation yield the desired list of finite subgroups of  .
.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of  is either
is either
- a cyclic group,
- a dihedral group, i.e.,
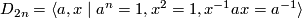 ,
, 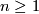 ,
,
- a tetrahedral group
 , i.e., the symmetry group of the regular tetrahedron,
, i.e., the symmetry group of the regular tetrahedron,
- a octahedral group
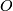 , i.e., the symmetry group of the regular octahedron,
, i.e., the symmetry group of the regular octahedron,
- a icosahedral group
 , i.e., the symmetry group of the regular icosahedron.
, i.e., the symmetry group of the regular icosahedron.
These groups are called polyhedral groups.
2.2 Finite subgroups of $S^3$
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider the action of
. Consider the action of  on
on  by conjugation
by conjugation
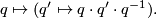
This action preserves  , so it descends to a norm-preserving action on the set of imaginary quaternions. Therefore this action yields a surjective representation
, so it descends to a norm-preserving action on the set of imaginary quaternions. Therefore this action yields a surjective representation 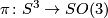 with kernel equal to
with kernel equal to 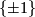 .
Hence,
.
Hence,  is a 2-fold covering map.
is a 2-fold covering map.
If  is a finite subgroup of
is a finite subgroup of  , let
, let 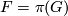 . If
. If 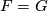 , then, since
, then, since  is the only element of
is the only element of  of order
of order  ,
,  and
and  must be both of odd order. Therefore comparing this with the list of finite subgroups of
must be both of odd order. Therefore comparing this with the list of finite subgroups of  yields that
yields that  and
and  are both cyclic of odd order. On the other hand, if
are both cyclic of odd order. On the other hand, if 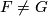 , then
, then  is an extension of the form
is an extension of the form
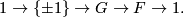
These considerations yields the following theorem.
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either
is either
- a cyclic group,
- a binary dihedral group,
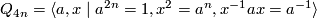 ,
, 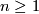 ,
,
- a binary tetrahedral group,
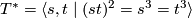 ,
,
- a binary octahedral group,
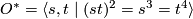 ,
,
- a binary icosahedralhedral group,
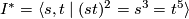 .
.
These groups are called binary polyhedral groups.
2.3 Finite subgroups of SO(4)
To perform the final step, consider the homomophism
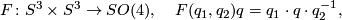
where 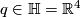 .
The kernel of
.
The kernel of  is equal to
is equal to 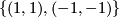 .
.
Finite subgroups of 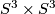 can be determined by Goursat's lemma. This lemma says, that every finite subgroup of
can be determined by Goursat's lemma. This lemma says, that every finite subgroup of 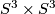 is isomorphic to the fibre product
is isomorphic to the fibre product 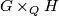 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 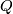 is a common quotient of
is a common quotient of  and
and  .
Consequently, any finite subgroup of
.
Consequently, any finite subgroup of  can be presented as a quotient
can be presented as a quotient 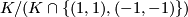 , where
, where 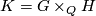 is the fiber product of two finite subgroups
is the fiber product of two finite subgroups  and
and  of
of  .
.
2.4 Finite fixed-point free subgroups of SO(4)
Not every finite subgroup of  can act freely on
can act freely on  . The Following lemma gives a necessary and sufficient condition for the map
. The Following lemma gives a necessary and sufficient condition for the map 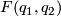 , defined in the previous section, to be fixed-point free for
, defined in the previous section, to be fixed-point free for 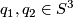 .
.
Lemma 2.3 [Wolf2011].
Let 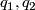 be unit quaternions, then
be unit quaternions, then 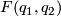 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 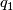 is conjgate to
is conjgate to 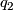 in
in  .
.
Proof. This is a simple observation
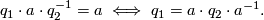

Using the above lemma and the classification of finite subgroups of  described in the previous section, we can obtain a complete list of finite, fixed-point free subgroups of
described in the previous section, we can obtain a complete list of finite, fixed-point free subgroups of  .
.
Theorem 2.4 [Wolf2011].
Any finite, fixed-point free subgroup of  belongs to the following list:
belongs to the following list:
- finite cyclic groups,
- generalised quaternion groups
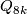 ,
, 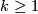 , i.e., a binary dihedral group (see Theorem 2.2 above) , where
, i.e., a binary dihedral group (see Theorem 2.2 above) , where 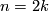 is even,
is even,
- the binary octahedral group
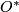 ,
,
- the binary tetrahedral group
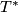 ,
,
- the binary icosahedral group
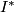 ,
,
- groups
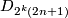 , for
, for  and
and 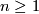 , with presentation
, with presentation
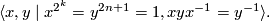
- groups
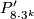 defined by the following presentation
defined by the following presentation
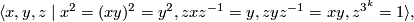
- direct product of any of the above groups with a cyclic group of relatively prime order.
3 Milnor's contribution
Milnor in [Milnor1957] proved the following theorem.
Theorem 3.1.
If  is a finite group which admits a fixed-point free action on a sphere
is a finite group which admits a fixed-point free action on a sphere 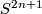 , then for every prime
, then for every prime  every subgroup of
every subgroup of  of order
of order 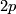 is cyclic.
is cyclic.
This theorem allowed him to choose all possible candidates, from the list compiled by Zassenhaus and Suzuki of groups with periodic cohomology, which could possibly act on  . Apart from groups which admit a fixed point free representation in
. Apart from groups which admit a fixed point free representation in  he obtained the following family of groups.
he obtained the following family of groups.
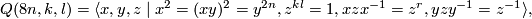
where 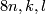 are relatively prime integers and
are relatively prime integers and
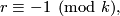
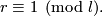
Groups 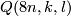 were excluded from the list of fundamental groups of
were excluded from the list of fundamental groups of  -manifolds only after resolution of the Geometrization Conjecture.
-manifolds only after resolution of the Geometrization Conjecture.
4 References
- [Hopf1926] H. Hopf, Zum Clifford-Kleinschen Raumproblem, Math. Ann. 95, (1926), 313-339. Zbl 51.0439.05
- [Milnor1957] J. Milnor, Groups which act on
 without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
without fixed points, Amer. J. Math. 79 (1957), 623–630. MR0090056 (19,761d)
- [Threlfall&Seifert1931] W. Threlfall and H. Seifert, Topologische Untersuchung der Diskontinuitätsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphärischen Raumes, Math. Ann. 104 (1931), no.1, 1–70. MR1512649 Zbl 0006.03403
- [Threlfall&Seifert1933] W. Threlfall and H. Seifert, Topologische Untersuchung der Diskontinuitätsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphärischen Raumes (Schluß), Math. Ann. 107 (1933), no.1, 543–586. MR1512817 Zbl 58.1203.01
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219