Space forms: a history
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:44, 13 May 2013 and the changes since publication. |
|
The user responsible for this page is Klaus Volkert. No other user may edit this page at present. |
Space forms, that is two-dimensional or three-dimensional Riemannian manifolds (later on they were generalized to n dimensions) which are locally isometric to the space of a classical geometry, were an important theme in early algebraic (or geometric) topology. Following a suggestion made by Killing (1891), they were called Clifford-Klein space forms ([Killing1891]).
Clifford-Klein space forms entered the history of mathematics in 1873 during a talk which was delivered by W. K. Clifford at the meeting of the British Association for the Advancement of Sciences (Bradford, in September 1873) and via an article he published in June 1873 ([Clifford1873]). The title of Clifford's talk was "On a surface of zero curvature and finite extension", the proceedings of the meeting only provide this title. But we know a bit more about it from F. Klein, who attended Clifford's talk and who described it on several occasions (for example [Klein1890] and [Klein1924, 154]). In the context of elliptic geometry - which Clifford conceived in Klein's way as the geometry of the part of projective space limited by a purely imaginary quartic - Clifford described a closed surface which is locally flat, the today so-called Clifford surface (this name was introduced by Klein ([Klein1890, 554])). This surface is constructed by using (today so called) Clifford parallels; Bianchi later provided a description by moving a circle along an elliptic straight line in such a way that it is always orthogonal to the straight line ([Bianchi1896, 105 - 107]). So Clifford's surface is the analogue of a cylinder; but - since it closed - it is often called a torus. To show its local flatness, Clifford used a dissection into parallelograms which is defined in a natural way by the two sets of parallels (or generators) contained in the surface. By considering the angles of such a parallelogram one sees that their sum equals four right angles so it is a common flat parallelogram. Clifford concluded: "The geometry of this surface is the same as that of a finite parallelogram whose opposite sides are regarded as identical." ([Clifford1873, 193]). This is a very early occurrence of the identification scheme for the torus!
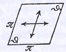
The term "Raumform" was used by W. Killing in his first mathematical research paper even in its title ([Killing1879]). Here he gave no explanation what he meant by this term; apparently it was Killing himself who introduced it as a technical term. The first use of this term by Killing is to be found in his review of Johannes Frischauf's book ([Frischauf1876]) on non-Euclidean geometry - the first real textbook of the new geometry in German - published by Killing in 1876 ([Killing1876]). But it should be noted that Frischauf himself had used the word "Raumform" at least on two occassions in his book ([Frischauf1876, 1 and 129]) indicating a sort of generalised space (there is one true space but several space forms). In his review Killing described Frischauf's intention in a very Killingean way (so to say): [In his new book of 1876, Frischauf] "wants to give a complete analysis of the geometric hypotheses and a comprehensive overview of all known results concerning those space-forms [sic!] which are independent of the parallel axiom. Truly a difficult enterprise." ([Killing1876, 464]). It was Killing who used the term space form over a period of 20 years before it became a standard term of mathematics. In the late 1870s he started a program to study all possible space forms in the sense described above in the citation. That is Killing wanted to determine all spaces which were compatible with the axioms of geometry. He admitted alternatives on two occasions: the axiom of the parallels and the axiom of straight lines (Killing's wording), that is the question, whether straight lines are infinite or not. Using Beltrami-Weierstrass coordinates he arrived at the conclusion that there are four such space forms: the Euclidean one, the hyperbolic one, the spherical and the elliptic one. His analysis is based on the assumption of (global) free mobility so it was natural to connect this result to constant curvature: there is one space form of constant zero curvature, one of constant negative curvature and two of constant positive curvature ([Killing1879]).
The results of his researches were presented by Killing in a more detailed and complete form in his book on space-forms ([Killing1885]). This book is remarkable because Killing gave a formula describing a torus embedded in ordinary 4-space which is locally flat - later called the flat torus ([Killing1885, 240-241]):
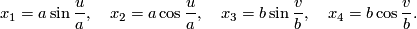
Using this representation it is easy to confirm by calculating 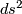 that the torus is locally flat. Killing remarked (in [Killing1893, 282 - 285]) that it is possible to choose the parameters
that the torus is locally flat. Killing remarked (in [Killing1893, 282 - 285]) that it is possible to choose the parameters  and
and  such that the torus is contained in
such that the torus is contained in  . In that case it can be projected into the elliptic space; the image of the flat torus is then nothing else but Clifford's surface.
. In that case it can be projected into the elliptic space; the image of the flat torus is then nothing else but Clifford's surface.
Space forms in the special sense just described - with global free mobility - are today often called spaces of constant curvature. In contrast to this, Killing's flat torus and Clifford's surface are today called Clifford-Klein space forms; they are only locally isometric to a classic geometric space, free mobility is restricted.
The study of these space forms was inaugurated by F. Klein with his article "Zur Nicht-Euklidischen Geometrie", which appeared 1890 in the "Mathematische Annalen" - more or less a summary of his lecture course on that theme delivered at Leipzig during the winter term of 1889 and the summer term of 1890. One section of this publication is devoted to Clifford's ideas, and in particular to his notion of parallelism and his surface. Klein observed that the principal difference between Clifford's surface and the usual Euclidean space is topological: Clifford's surface is "multiply connected" whereas the latter is simply connected. Klein commented: "This result is remarkable, because it contradicts our usual idea of the properties of an unlimited manifold of zero curvature. ... obviously this is related to the fact that Clifford's surface - ... - has a multiple connection." ([Klein1890, 554]).
Klein discussed other examples of flat surfaces; he supposed that they were all gained by pairwise identifications of the sides of a strip or of a rectangle. So he got the cylinder, the flat torus and the today so-called Klein bottle (he missed the unlimited Möbius band, cf. below). He also discussed the case of positive constant curvature where he found the sphere and the elliptic plane. The case of constant negative curvature is left open by Klein. He restricted himself mainly to the case of surfaces, that is of two-dimensional space forms.
An important step was taken by W. Killing one year after Klein. In his paper ([Killing1891]) Killing established the connection between space forms and suitable subgroups of the groups of isometries of classical geometries (that is hyperbolic, Euclidean, spherical and elliptic): Using modern terms a space form is provided by passing to the homogenuous space 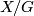 where
where  is such a classical space (in principle there is no restriction on its dimension so it may be
is such a classical space (in principle there is no restriction on its dimension so it may be  -dimensional) and
-dimensional) and  is a group of isometries which operates discontinuously (that is without points of accumulation) and freely (that there is no point left invariant by any non-identity element of the group). Groups like that were known from the theory of automorphic functions founded by Klein and Poincaré at the beginnings of the 1880s. By this insight it became possible to construct new space forms. These ideas are discussed at length in Killing's book ([Killing1893, chap. 4]), in his paper there were only short hints at them. The examples provided by Killing are more or less the same as those given by Klein - a difference is that Killing missed the non-orientable case. It should be noted that Killing stressed the difference between global and local free mobility; this was even the starting point for his investigations.
is a group of isometries which operates discontinuously (that is without points of accumulation) and freely (that there is no point left invariant by any non-identity element of the group). Groups like that were known from the theory of automorphic functions founded by Klein and Poincaré at the beginnings of the 1880s. By this insight it became possible to construct new space forms. These ideas are discussed at length in Killing's book ([Killing1893, chap. 4]), in his paper there were only short hints at them. The examples provided by Killing are more or less the same as those given by Klein - a difference is that Killing missed the non-orientable case. It should be noted that Killing stressed the difference between global and local free mobility; this was even the starting point for his investigations.
The state of the art was summarized by Enriques in his article for Klein's "Enzyklopädie der mathematischen Wissenschaften"; but Enriques' list for the two-dimensional case is the same as that given by Klein ([Enriques1907, 115 - 117]).
A remarkable step was taken by H. Weyl in 1916. In the appendix of his article ([Weyl1916]) he proved that locally flat space forms - Weyl called them "crystals" - are exactly those which are constructed by the passage to an homogeneous space described by Killing. In his proof Weyl used the technique of universal covering spaces including fundamental groups and groups of deck transformations and their relations ([Weyl1916]). The idea is this: Construct the universal covering space of the flat Clifford-Klein space form and show that it is isometric to the space of a classical geometry.
In 1925 H. Hopf again took up the question in generalizing Weyl's technique to all types of Clifford-Klein space forms ([Hopf1926]). He also gave the complete list of flat surfaces in adding the "infinite" Möbius band to the list. Particular attention was payed by Hopf to the case of three-dimensional spherical space forms. He solve this problem by using the homomorphism
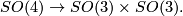
This was the starting for Hopf's research which lead him to the discovery of the Hopf fibration.
The question of three-dimensional spherical Clifford-Klein space forms was studied independently from Hopf by H. Seifert and W. Threlfall in their joint papers ([Threlfall&Seifert1931],[Threlfall&Seifert1933]; cf. also [Volkert2002], [Volkert2005]). They were at the origin of Seifert's theory of fibered spaces. The problem of three-dimensional flat Clifford-Klein space forms was investigated by two students of Seifert and Threlfall, W. Hantzsche and H. Wendt ([Hantzsche&Wendt1934]); they used important results by L. Bieberbach ([Bieberbach1911], [Bieberbach1912]). The first three-dimensional hyperbolic Clifford-Klein space form was constructed by H. Gieseking ([Gieseking1912]); another one - called the hyperbolic dodecahedron space - was constructed by C. Weber and H. Seifert in 1933 ([Weber&Seifert1933]).
From its very beginning the discussion of space forms was related to the question of our empirical knowledge. Because the latter is always local, it is clear that we are not able to distinguish between a large enough flat Clifford-Klein space form and Euclidean space (for example). In one of the first papers on the elliptic space form the US-astronomer S. Newcomb wrote: "It may be also remarked that there is nothing within our experience which will justify a denial of the possibility that the space in which we find ourselves may be curved in the manner here supposed." ([Newcomb1877], 299). In the year 1900, K. Schwarzschild came back to this possibility in his often cited article ([Schwarzschild1900]), supplying some more precise astronomical data but no substantial new idea. For a modern discussion of this topic cf. [Luminet2005].
For more details on the history of space forms cf. [Epple2002] or [Volkert2002]; a detailed study is forthcoming: [Volkert2013].
References
- [Bianchi1896] L. Bianchi, Sulle superficie a curvatura nulla in geometria ellittica., Annali di Mat. (1896) 93-123. Zbl 27.0370.02
- [Bieberbach1911] L. Bieberbach, Über die Bewegungsgruppen der Euklidischen Räume. (Erste Abh.)., (German) Math. Ann. 70, (1911), 297–336 MR1511704 Zbl 42.0144.02
- [Bieberbach1912] L. Bieberbach, Über die Bewegungsgruppen der euklidischen Räume. (Zweite Abhandlung.) Die Gruppen mit einem endlichen Fundamentalbereich., (German) Math. Ann. 72, (1912), 400-412. MR1511704 Zbl 43.0186.01
- [Clifford1873] W. K. Clifford, Preliminary sketch of biquaternons., Proc. of L. M. S. IV. (1873), 381-395. Zbl 05.0280.01
- [Enriques1907] F. Enriques, Prinzipien der Geometrie., 4Enzyklop. d. math. Wissensch.
 , (1907), 1-129. Zbl 38.0496.01
, (1907), 1-129. Zbl 38.0496.01
- [Epple2002] M. Epple, From quaternions to cosmology: spaces of constant curvature, ca. 1873-1925, Proceedings of the International Congress of Mathematicians, Vol. III (2002), 935–945. MR1957592 (2004a:01018) Zbl 0997.01005
- [Frischauf1876] J. Frischauf, Elemente der absoluten Geometrie., Leipzig, 1876. Zbl 08.0313.01
- [Gieseking1912] H. Gieseking, Analytische Untersuchungen über topologische Gruppen., Hilchenbach, 1912. Zbl 43.0202.03
- [Hantzsche&Wendt1934] W. Hantzsche and H. Wendt, Dreidimensionale euklidische Raumformen., (German) Math. Ann. 110 (1934), no.1, 593-611. MR1512956 Zbl 0010.18003
- [Hopf1926] H. Hopf, Zum Clifford-Kleinschen Raumproblem, Math. Ann. 95, (1926), 313-339. Zbl 51.0439.05
- [Killing1876] W. Killing, Review of [Frischauf1876], in Zeitschrift für den mathematischen und naturwissenschaftlichen Unterricht 7 (1876), 464 - 469.
- [Killing1879] W. Killing, Ueber zwei Raumformen mit constanter Krümmung, J. Reine Angew. Math., 86 (1879), 72-83. MR1579765 Zbl 10.0344.01
- [Killing1885] W. Killing, Die nichteuklidischen Raumformen in analytischer Behandlung., Leipzig, 1885. Zbl 17.0508.01
- [Killing1891] W. Killing, Ueber die Clifford-Klein'schen Raumformen., (German) Math. Ann. 39 (1891), 257-270. MR1510701 Zbl 23.0529.01
- [Killing1893] W. Killing, Einführung in die Grundlagen der Geometrie. I. Band, Paderborn. F. Schöningh. 1893. Zbl 25.0853.01
- [Klein1890] F. Klein, Zur Nicht-Euklidischen Geometrie, Math. Ann. 37 (1890), 544-572. Zbl 22.0535.01
- [Klein1924] F. Klein, Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Ausgabe in einem Band. Reprint., Grundlehren der mathematischen Wissenschaften. Band XXIV und XXV. Berlin-Heidelberg-New York: Springer-Verlag. XIII, 1979. MR0529278 (82c:01027) Zbl 0398.01006
- [Luminet2005] J. P. Luminet, Topologie et cosmologie, in Geometry in the 20th century, 1930–2000 History and horizons (Géométrie au XXe siècle, 1930–2000 Histoire et horizons), Paris: Hermann. 2005, 351-361.
- [Newcomb1877] S. Newcomb, Elementary theorems relating to the geometry of a space of three dimensions and of uniform positive curvature in the fourth dimension., J. Reine Angew. Math. 83 (1877), 293-300. Zbl 09.0381.03
- [Schwarzschild1900] K. Schwarzschild, Ueber das zulässige Krümmungsmass des Raumes., Vierteljahrsschr. Astr. Ges. 35, (1900), 337-347. Zbl 31.0892.06
- [Threlfall&Seifert1931] W. Threlfall and H. Seifert, Topologische Untersuchung der Diskontinuitätsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphärischen Raumes, Math. Ann. 104 (1931), no.1, 1–70. MR1512649 Zbl 0006.03403
- [Threlfall&Seifert1933] W. Threlfall and H. Seifert, Topologische Untersuchung der Diskontinuitätsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphärischen Raumes (Schluß), Math. Ann. 107 (1933), no.1, 543–586. MR1512817 Zbl 58.1203.01
- [Volkert2002] K. Volkert, Das Homöomorphieproblem insbesondere der 3-Mannigfaltigkeiten, in der Topologie 1892 - 1935, Paris, 2002.
- [Volkert2005] K. Volkert, Le retour de la géométrie, in Géométrie au XXe siècle, ed. by J. Kouneiher, D. Flament, P. Nabonnand and J. Szczeciniarz (Paris, 2005), 150–162.
- [Volkert2013] K. Volkert, Ways of making space. The early history of space-forms from Clifford to Klein, in: Lisa Bioesmat-Martagon: Eléments d'une biographie de l'espace mathématique (Nancy: PUN forthcoming) (2013).
- [Weber&Seifert1933] C. Weber and H. Seifert, Die beiden Dodekaederräume, Math. Z. 37 (1933), no.1, 237–253. MR1545392 Zbl 0007.02806
- [Weyl1916] H. Weyl, Über die Gleichverteilung von Zahlen mod. Eins., (German) Math. Ann. 77 (1916), 313-352. MR1511862 Zbl 46.0278.06