Fundamental groups of 3-dimensional spherical space forms
|
The user responsible for this page is Wpolitarczyk. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
The purpose of this article is to describe fundamental groups of  -dimensional spherical space forms. For the historical context refer to this article. Fundamental groups of
-dimensional spherical space forms. For the historical context refer to this article. Fundamental groups of  -dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into
-dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into  thus yielding a
thus yielding a  -manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into
-manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into  , yet they can act without fixed points on
, yet they can act without fixed points on  . The exposition is based on [Wolf2011].
. The exposition is based on [Wolf2011].
2 Finite subgroups of $SO(4)$
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
 ,
,
- use the covering map
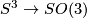 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 doubly covers
doubly covers Tex syntax error
to determine its finite groups.
2.1 Finite subgroups of $SO(3)$
First step in the determination of the groups from first family is the classification of finite subgroups of  . This is done by analysing the action of this group on
. This is done by analysing the action of this group on  . From Riemann-Hurwitz formula we obtain an equation
. From Riemann-Hurwitz formula we obtain an equation
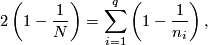
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 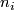 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of  is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
2.2 Finite subgroups of $S^3$
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
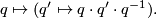
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 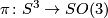 with kernel equal to
with kernel equal to 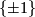 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 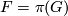 . If
. If 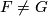 , then, since
, then, since  is the only element of
is the only element of  of order
of order  ,
,  and
and  are of odd order. Therefore
are of odd order. Therefore 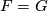 is cyclic of odd order. If
is cyclic of odd order. If 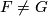 , then
, then  is an extension of the form
is an extension of the form
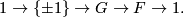
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
2.3 Finite subgroups of $SO(4)$
To perform the final step, consider a homomophism
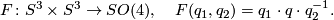
Its kernel is equal to 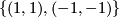 .
.
Tex syntax errorcan be determined by Goursat's lemma. This lemma says, that every finite subgroup of
Tex syntax erroris isomorphic to the fibre product
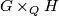 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 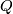 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of $SO(4)$
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 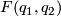 to be fixed point free for
to be fixed point free for 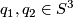 .
.
Lemma 2.3 [Wolf2011].
Let 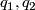 be unit quaternions, then
be unit quaternions, then 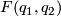 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 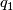 is conjgate to
is conjgate to 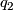 in
in  .
.
Proof. This is a simple observation
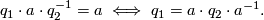

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
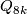 ,
,
- binary tetrahedral group
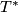 ,
,
- binary icosahedral group
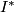 ,
,
- groups
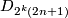 , for
, for  and
and 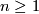 , with presentation
, with presentation
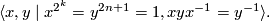
- groups
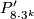 defined by the following presentation
defined by the following presentation
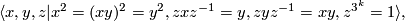
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
4 References
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219
 -dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into
-dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into  thus yielding a
thus yielding a  -manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into
-manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into  , yet they can act without fixed points on
, yet they can act without fixed points on  . The exposition is based on [Wolf2011].
. The exposition is based on [Wolf2011].
2 Finite subgroups of $SO(4)$
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
 ,
,
- use the covering map
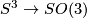 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 doubly covers
doubly covers Tex syntax error
to determine its finite groups.
2.1 Finite subgroups of $SO(3)$
First step in the determination of the groups from first family is the classification of finite subgroups of  . This is done by analysing the action of this group on
. This is done by analysing the action of this group on  . From Riemann-Hurwitz formula we obtain an equation
. From Riemann-Hurwitz formula we obtain an equation
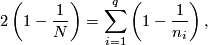
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 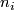 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of  is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
2.2 Finite subgroups of $S^3$
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
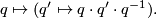
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 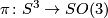 with kernel equal to
with kernel equal to 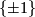 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 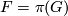 . If
. If 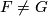 , then, since
, then, since  is the only element of
is the only element of  of order
of order  ,
,  and
and  are of odd order. Therefore
are of odd order. Therefore 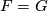 is cyclic of odd order. If
is cyclic of odd order. If 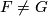 , then
, then  is an extension of the form
is an extension of the form
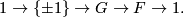
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
2.3 Finite subgroups of $SO(4)$
To perform the final step, consider a homomophism
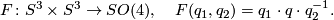
Its kernel is equal to 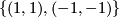 .
.
Tex syntax errorcan be determined by Goursat's lemma. This lemma says, that every finite subgroup of
Tex syntax erroris isomorphic to the fibre product
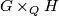 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 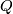 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of $SO(4)$
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 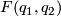 to be fixed point free for
to be fixed point free for 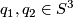 .
.
Lemma 2.3 [Wolf2011].
Let 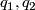 be unit quaternions, then
be unit quaternions, then 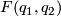 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 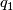 is conjgate to
is conjgate to 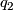 in
in  .
.
Proof. This is a simple observation
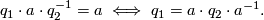

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
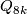 ,
,
- binary tetrahedral group
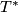 ,
,
- binary icosahedral group
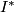 ,
,
- groups
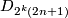 , for
, for  and
and 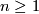 , with presentation
, with presentation
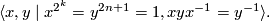
- groups
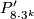 defined by the following presentation
defined by the following presentation
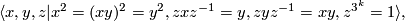
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
4 References
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219
 -dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into
-dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into  thus yielding a
thus yielding a  -manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into
-manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into  , yet they can act without fixed points on
, yet they can act without fixed points on  . The exposition is based on [Wolf2011].
. The exposition is based on [Wolf2011].
2 Finite subgroups of $SO(4)$
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
 ,
,
- use the covering map
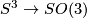 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 doubly covers
doubly covers Tex syntax error
to determine its finite groups.
2.1 Finite subgroups of $SO(3)$
First step in the determination of the groups from first family is the classification of finite subgroups of  . This is done by analysing the action of this group on
. This is done by analysing the action of this group on  . From Riemann-Hurwitz formula we obtain an equation
. From Riemann-Hurwitz formula we obtain an equation
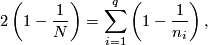
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 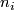 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of  is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
2.2 Finite subgroups of $S^3$
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
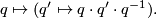
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 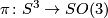 with kernel equal to
with kernel equal to 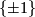 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 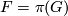 . If
. If 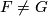 , then, since
, then, since  is the only element of
is the only element of  of order
of order  ,
,  and
and  are of odd order. Therefore
are of odd order. Therefore 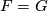 is cyclic of odd order. If
is cyclic of odd order. If 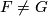 , then
, then  is an extension of the form
is an extension of the form
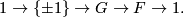
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
2.3 Finite subgroups of $SO(4)$
To perform the final step, consider a homomophism
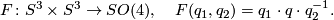
Its kernel is equal to 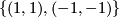 .
.
Tex syntax errorcan be determined by Goursat's lemma. This lemma says, that every finite subgroup of
Tex syntax erroris isomorphic to the fibre product
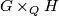 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 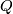 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of $SO(4)$
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 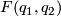 to be fixed point free for
to be fixed point free for 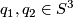 .
.
Lemma 2.3 [Wolf2011].
Let 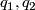 be unit quaternions, then
be unit quaternions, then 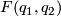 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 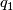 is conjgate to
is conjgate to 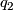 in
in  .
.
Proof. This is a simple observation
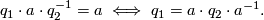

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
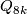 ,
,
- binary tetrahedral group
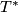 ,
,
- binary icosahedral group
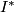 ,
,
- groups
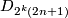 , for
, for  and
and 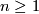 , with presentation
, with presentation
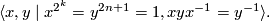
- groups
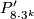 defined by the following presentation
defined by the following presentation
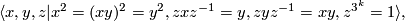
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
4 References
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219
 -dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into
-dimensional spherical space forms can be divided into two families. First family consists of groups which admit a linear fixed-point free representation into  thus yielding a
thus yielding a  -manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into
-manifold admitting riemannian metric of constant curvature. Second family consists of groups which do not admit a representation into  , yet they can act without fixed points on
, yet they can act without fixed points on  . The exposition is based on [Wolf2011].
. The exposition is based on [Wolf2011].
2 Finite subgroups of $SO(4)$
To determine finite subgroups of  it is necessary to proceed in three steps:
it is necessary to proceed in three steps:
- determine finite subgroups of
 ,
,
- use the covering map
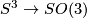 to determine finite subgroups of
to determine finite subgroups of  ,
,
- use the fact that
 doubly covers
doubly covers Tex syntax error
to determine its finite groups.
2.1 Finite subgroups of $SO(3)$
First step in the determination of the groups from first family is the classification of finite subgroups of  . This is done by analysing the action of this group on
. This is done by analysing the action of this group on  . From Riemann-Hurwitz formula we obtain an equation
. From Riemann-Hurwitz formula we obtain an equation
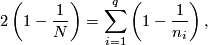
where  denotes the order of the group,
denotes the order of the group,  denotes number of orbits with non-trivial isotropy and
denotes number of orbits with non-trivial isotropy and 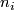 denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
denotes the order of the respective isotropy subgroup. Solutions to this equation yield the desired list.
Theorem 2.1 [Wolf2011, thm 2.6.5.].
Every finite subgroup of  is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
is either cyclic, dihedral, tetrahedral, octahedral or icosahedral.
2.2 Finite subgroups of $S^3$
Let  denote the algebra of quaternions and treat
denote the algebra of quaternions and treat  as a subset of
as a subset of  of quaternions of norm
of quaternions of norm  . Consider an action of
. Consider an action of  on
on  by conjugation
by conjugation
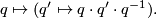
This action preserves  , so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation
, so it induces an action on the set of imaginary quaternions which preserves the norm. Therefore this action yields a representation 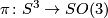 with kernel equal to
with kernel equal to 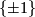 .
.
If  is a finite subgroup of
is a finite subgroup of  , then let
, then let 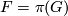 . If
. If 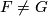 , then, since
, then, since  is the only element of
is the only element of  of order
of order  ,
,  and
and  are of odd order. Therefore
are of odd order. Therefore 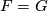 is cyclic of odd order. If
is cyclic of odd order. If 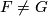 , then
, then  is an extension of the form
is an extension of the form
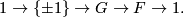
Theorem 2.2 [Wolf2011].
Every finite subgroup of  is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
is either cyclic group, binary dihedral group, binary tetrahedral group, binary octahedral group or binary icosahedralhedral group.
2.3 Finite subgroups of $SO(4)$
To perform the final step, consider a homomophism
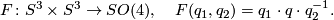
Its kernel is equal to 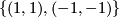 .
.
Tex syntax errorcan be determined by Goursat's lemma. This lemma says, that every finite subgroup of
Tex syntax erroris isomorphic to the fibre product
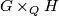 , where
, where  and
and  are finite subgroups of
are finite subgroups of  and
and 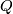 is a common quotient of
is a common quotient of  and
and  .
.
2.4 Finite fixed-point free subgroups of $SO(4)$
Not every finite subgroup of  act freely on
act freely on  . Following lemma gives necessary and sufficient condition for
. Following lemma gives necessary and sufficient condition for 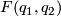 to be fixed point free for
to be fixed point free for 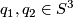 .
.
Lemma 2.3 [Wolf2011].
Let 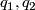 be unit quaternions, then
be unit quaternions, then 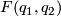 has a fixed point on
has a fixed point on  if, and only if,
if, and only if, 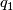 is conjgate to
is conjgate to 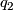 in
in  .
.
Proof. This is a simple observation
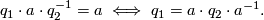

Theorem 2.4 [Wolf2011].
Finite fixed-point free subgroup of  belongs to the following list
belongs to the following list
- cyclic group,
- generalised quaternion group
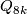 ,
,
- binary tetrahedral group
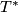 ,
,
- binary icosahedral group
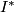 ,
,
- groups
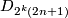 , for
, for  and
and 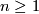 , with presentation
, with presentation
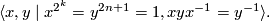
- groups
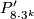 defined by the following presentation
defined by the following presentation
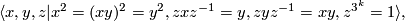
- direct product of any of the above group with a cyclic group of relatively prime order.
3 Milnor's contribution
4 References
- [Wolf2011] J. A. Wolf, Spaces of constant curvature, AMS Chelsea Publishing, Providence, RI, 2011. MR2742530 (2011j:53001) Zbl 05830219