Fake lens spaces
(→Homotopy Classification) |
(→Homotopy Classification) |
||
| Line 87: | Line 87: | ||
The existence of a fake lens space in the homotopy type of such $L$ | The existence of a fake lens space in the homotopy type of such $L$ | ||
| − | is addressed in | + | is addressed in {{cite|Wall1999|Theorem 14E.4}}. |
Since the units $\varepsilon' (u) \in \Zz_N$ are exhausted by the lens spaces | Since the units $\varepsilon' (u) \in \Zz_N$ are exhausted by the lens spaces | ||
Revision as of 17:31, 7 June 2010
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:18, 25 April 2013 and the changes since publication. |
Contents |
1 Introduction
A fake lens space is the orbit space of a free action of a finite cyclic group 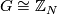 on a sphere
on a sphere 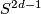 . It is a generalization of the notion of a lens space which is
the orbit space of a free action which comes from a unitary representation.
. It is a generalization of the notion of a lens space which is
the orbit space of a free action which comes from a unitary representation.
2 Construction and examples
- ...
3 Invariants
-
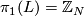 ,
, 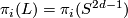 for
for 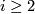
-
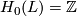 ,
, 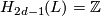 ,
, 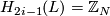 for
for 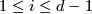 ,
, 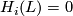 for all other values of
for all other values of  .
.
-
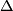 ,
,  , ...
, ...
4 Homotopy Classification
All the results are taken from chapter 14E of [Wall1999].
Notation
Recall the arithmetic (Rim) square:
![\displaystyle \xymatrix{ \Zz G \ar[r]^{\eta} \ar[d]_{\varepsilon} & R_G \ar[d]^{\varepsilon'} \\ \Zz \ar[r]_{\eta'} & \Zz_N }](/images/math/3/4/d/34da3249bf4eb2eac0505f1c05c1a32f.png)
where 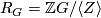 with
with 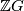 be the group ring of
be the group ring of  and
and 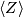 is the ideal generated by the norm element
is the ideal generated by the norm element 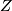 of
of  . The maps
. The maps  ,
, 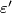 are the augmentation maps.
are the augmentation maps.
Recall that the Reidemeister torsion is a unit in 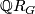 where
where 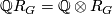 .
.
The homotopy classification is stated in the a priori broader context of finite CW-complexes  with
with 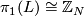 and with the universal cover homotopy equivalent to
and with the universal cover homotopy equivalent to 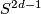 of which fake lens spaces are obviously a special case. It is convenient to make the
following definition.
of which fake lens spaces are obviously a special case. It is convenient to make the
following definition.
Definition 4.1.
Let  be a CW-complex with
be a CW-complex with 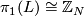 and with universal cover homotopy equivalent to
and with universal cover homotopy equivalent to 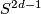 .
.
A polarization of  is a pair
is a pair 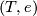 where
where  is a choice of a generator of
is a choice of a generator of 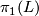 and
and  is a choice of a homotopy equivalence
is a choice of a homotopy equivalence 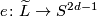 .
.
Recall the classical lens space 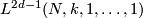 . By
. By 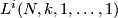 is denoted its
is denoted its  -skeleton with respect to the standard cell decomposition. If
-skeleton with respect to the standard cell decomposition. If  is odd this is a lens space, if
is odd this is a lens space, if  is even this is a CW-complex obtained by attaching an
is even this is a CW-complex obtained by attaching an  -cell to the lens space of dimension
-cell to the lens space of dimension 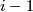 .
.
Proposition 4.2.
Let  be a finite CW-complex with
be a finite CW-complex with 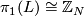 and universal cover
and universal cover 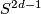 polarized by
polarized by 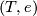 . Then there exists a simple homotopy equivalence
. Then there exists a simple homotopy equivalence
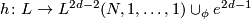
preserving the polarization. It is unique up to homotopy and the
action of  . The chain complex differential on the right hand side
is given by
. The chain complex differential on the right hand side
is given by 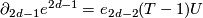 for some
for some
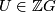 which maps to a unit
which maps to a unit 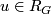 . Furthermore,
. Furthermore,  is a simple Poincare complex with Reidemeister torsion
is a simple Poincare complex with Reidemeister torsion 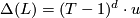 .
.
- The polarized homotopy types of such
 are in one-to-one correspondence with the units in
are in one-to-one correspondence with the units in 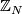 . The correspondence is given by
. The correspondence is given by 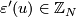 . The invariant
. The invariant 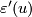 can be identified with the first non-trivial
can be identified with the first non-trivial  -invariant of
-invariant of  (in the sense of homotopy theory)
(in the sense of homotopy theory) 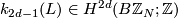 .
.
- The polarized simple homotopy types of such
 are in one-to-one correspondence with the units in
are in one-to-one correspondence with the units in 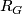 . The correspondence is given by
. The correspondence is given by 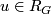 .
.
See Theorem 14E.3 in [Wall1999].
The existence of a fake lens space in the homotopy type of such  is addressed in [Wall1999, Theorem 14E.4].
is addressed in [Wall1999, Theorem 14E.4].
Since the units 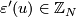 are exhausted by the lens spaces
are exhausted by the lens spaces
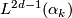 we obtain the following corollary.
we obtain the following corollary.
Corollary 4.3.
For any fake lens space 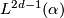 there exists
there exists 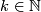 and a homotopy equivalence
and a homotopy equivalence
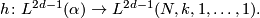
5 Homeomorphism classification
There is the following commutative diagram of abelian groups and homomorphisms with exact rows
![\displaystyle \xymatrix{ 0 \ar[r] & {\widetilde L}^s_{2d} (G) \ar[r]^(0.4){\partial} \ar[d]_{\cong}^{G-sign} & {\mathcal S}^s (L^{2d-1}(\alpha)) \ar[r]^{\eta} \ar[d]^{\widetilde \rho}& \widetilde {\mathcal N} (L^{2d-1}(\alpha)) \ar[r] \ar[d]^{[\widetilde \rho]}& 0 \\ 0 \ar[r] & 4 \cdot R^{(-1)^d}_{\widehat G} \ar[r] & {\mathbb Q} R^{(-1)^d}_{\widehat G} \ar[r] & {\mathbb Q} R^{(-1)^d}_{\widehat G}/ 4 \cdot R^{(-1)^d}_{\widehat G} \ar[r] & 0 }](/images/math/c/e/0/ce0adafd80f8f574c18c1ece6266bff7.png)
where ![[\widetilde \rho]](/images/math/1/a/6/1a65cbd449686c64de628afc09f22dd2.png) is the homomorphism induced by
is the homomorphism induced by 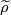 (see ?).
(see ?).
The map 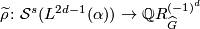 is injective if
is injective if 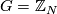 with
with  odd (compare [Wall1999, Corollary on page 222]?).
odd (compare [Wall1999, Corollary on page 222]?).
The following theorem is taken from [Wall1999, Theorem 14E.7].
Theorem 5.1.
Let 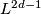 and
and 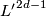 be oriented fake lens spaces with fundamental group
be oriented fake lens spaces with fundamental group  cyclic of odd order
cyclic of odd order  . Then there is an orientation preserving homeomorphism
. Then there is an orientation preserving homeomorphism 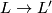 inducing the identity on
inducing the identity on  if and only if
if and only if 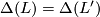 and
and 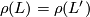 .
.
Given 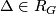 and
and 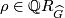 , there exists a corresponding fake lens space
, there exists a corresponding fake lens space 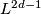 if and only if the following four statements hold:
if and only if the following four statements hold:
-
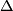 and
and  are both real (
are both real ( even) or imaginary (
even) or imaginary ( odd).
odd).
-
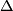 generates ...
generates ...
- ...
- ...
The following theorem is proved in [Macko&Wegner2010, Theorem 1.2]).
Theorem 5.2.
Let 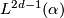 be a fake lens space with
be a fake lens space with 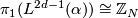 where
where 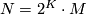 with
with 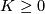 ,
,  odd and
odd and 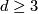 . Then we have
. Then we have
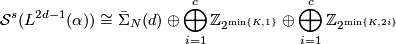
where 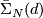 is a free abelian group. If
is a free abelian group. If  is odd then its rank is
is odd then its rank is 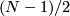 . If
. If  is even then its rank is
is even then its rank is 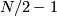 if
if 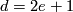 and
and 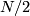 if
if 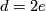 . In the torsion summand we have
. In the torsion summand we have 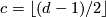 .
.
6 Further discussion
- ...
7 References
- [Macko&Wegner2010] Template:Macko&Wegner2010
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003
|
This page has not been refereed. The information given here might be incomplete or provisional. |
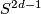 . It is a generalization of the notion of a lens space which is
the orbit space of a free action which comes from a unitary representation.
. It is a generalization of the notion of a lens space which is
the orbit space of a free action which comes from a unitary representation.
2 Construction and examples
- ...
3 Invariants
-
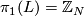 ,
, 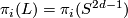 for
for 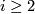
-
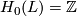 ,
, 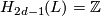 ,
, 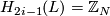 for
for 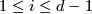 ,
, 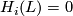 for all other values of
for all other values of  .
.
-
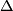 ,
,  , ...
, ...
4 Homotopy Classification
All the results are taken from chapter 14E of [Wall1999].
Notation
Recall the arithmetic (Rim) square:
![\displaystyle \xymatrix{ \Zz G \ar[r]^{\eta} \ar[d]_{\varepsilon} & R_G \ar[d]^{\varepsilon'} \\ \Zz \ar[r]_{\eta'} & \Zz_N }](/images/math/3/4/d/34da3249bf4eb2eac0505f1c05c1a32f.png)
where 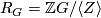 with
with 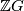 be the group ring of
be the group ring of  and
and 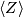 is the ideal generated by the norm element
is the ideal generated by the norm element 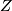 of
of  . The maps
. The maps  ,
, 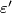 are the augmentation maps.
are the augmentation maps.
Recall that the Reidemeister torsion is a unit in 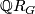 where
where 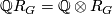 .
.
The homotopy classification is stated in the a priori broader context of finite CW-complexes  with
with 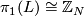 and with the universal cover homotopy equivalent to
and with the universal cover homotopy equivalent to 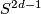 of which fake lens spaces are obviously a special case. It is convenient to make the
following definition.
of which fake lens spaces are obviously a special case. It is convenient to make the
following definition.
Definition 4.1.
Let  be a CW-complex with
be a CW-complex with 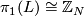 and with universal cover homotopy equivalent to
and with universal cover homotopy equivalent to 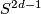 .
.
A polarization of  is a pair
is a pair 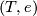 where
where  is a choice of a generator of
is a choice of a generator of 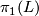 and
and  is a choice of a homotopy equivalence
is a choice of a homotopy equivalence 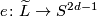 .
.
Recall the classical lens space 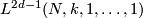 . By
. By 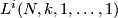 is denoted its
is denoted its  -skeleton with respect to the standard cell decomposition. If
-skeleton with respect to the standard cell decomposition. If  is odd this is a lens space, if
is odd this is a lens space, if  is even this is a CW-complex obtained by attaching an
is even this is a CW-complex obtained by attaching an  -cell to the lens space of dimension
-cell to the lens space of dimension 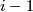 .
.
Proposition 4.2.
Let  be a finite CW-complex with
be a finite CW-complex with 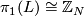 and universal cover
and universal cover 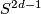 polarized by
polarized by 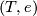 . Then there exists a simple homotopy equivalence
. Then there exists a simple homotopy equivalence
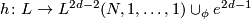
preserving the polarization. It is unique up to homotopy and the
action of  . The chain complex differential on the right hand side
is given by
. The chain complex differential on the right hand side
is given by 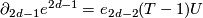 for some
for some
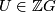 which maps to a unit
which maps to a unit 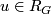 . Furthermore,
. Furthermore,  is a simple Poincare complex with Reidemeister torsion
is a simple Poincare complex with Reidemeister torsion 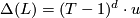 .
.
- The polarized homotopy types of such
 are in one-to-one correspondence with the units in
are in one-to-one correspondence with the units in 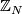 . The correspondence is given by
. The correspondence is given by 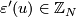 . The invariant
. The invariant 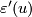 can be identified with the first non-trivial
can be identified with the first non-trivial  -invariant of
-invariant of  (in the sense of homotopy theory)
(in the sense of homotopy theory) 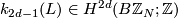 .
.
- The polarized simple homotopy types of such
 are in one-to-one correspondence with the units in
are in one-to-one correspondence with the units in 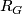 . The correspondence is given by
. The correspondence is given by 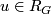 .
.
See Theorem 14E.3 in [Wall1999].
The existence of a fake lens space in the homotopy type of such  is addressed in [Wall1999, Theorem 14E.4].
is addressed in [Wall1999, Theorem 14E.4].
Since the units 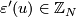 are exhausted by the lens spaces
are exhausted by the lens spaces
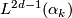 we obtain the following corollary.
we obtain the following corollary.
Corollary 4.3.
For any fake lens space 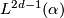 there exists
there exists 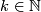 and a homotopy equivalence
and a homotopy equivalence
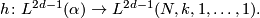
5 Homeomorphism classification
There is the following commutative diagram of abelian groups and homomorphisms with exact rows
![\displaystyle \xymatrix{ 0 \ar[r] & {\widetilde L}^s_{2d} (G) \ar[r]^(0.4){\partial} \ar[d]_{\cong}^{G-sign} & {\mathcal S}^s (L^{2d-1}(\alpha)) \ar[r]^{\eta} \ar[d]^{\widetilde \rho}& \widetilde {\mathcal N} (L^{2d-1}(\alpha)) \ar[r] \ar[d]^{[\widetilde \rho]}& 0 \\ 0 \ar[r] & 4 \cdot R^{(-1)^d}_{\widehat G} \ar[r] & {\mathbb Q} R^{(-1)^d}_{\widehat G} \ar[r] & {\mathbb Q} R^{(-1)^d}_{\widehat G}/ 4 \cdot R^{(-1)^d}_{\widehat G} \ar[r] & 0 }](/images/math/c/e/0/ce0adafd80f8f574c18c1ece6266bff7.png)
where ![[\widetilde \rho]](/images/math/1/a/6/1a65cbd449686c64de628afc09f22dd2.png) is the homomorphism induced by
is the homomorphism induced by 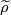 (see ?).
(see ?).
The map 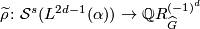 is injective if
is injective if 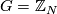 with
with  odd (compare [Wall1999, Corollary on page 222]?).
odd (compare [Wall1999, Corollary on page 222]?).
The following theorem is taken from [Wall1999, Theorem 14E.7].
Theorem 5.1.
Let 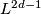 and
and 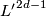 be oriented fake lens spaces with fundamental group
be oriented fake lens spaces with fundamental group  cyclic of odd order
cyclic of odd order  . Then there is an orientation preserving homeomorphism
. Then there is an orientation preserving homeomorphism 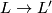 inducing the identity on
inducing the identity on  if and only if
if and only if 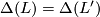 and
and 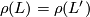 .
.
Given 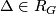 and
and 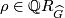 , there exists a corresponding fake lens space
, there exists a corresponding fake lens space 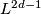 if and only if the following four statements hold:
if and only if the following four statements hold:
-
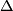 and
and  are both real (
are both real ( even) or imaginary (
even) or imaginary ( odd).
odd).
-
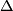 generates ...
generates ...
- ...
- ...
The following theorem is proved in [Macko&Wegner2010, Theorem 1.2]).
Theorem 5.2.
Let 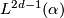 be a fake lens space with
be a fake lens space with 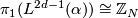 where
where 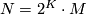 with
with 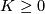 ,
,  odd and
odd and 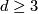 . Then we have
. Then we have
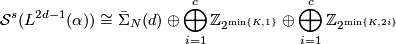
where 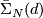 is a free abelian group. If
is a free abelian group. If  is odd then its rank is
is odd then its rank is 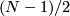 . If
. If  is even then its rank is
is even then its rank is 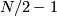 if
if 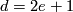 and
and 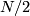 if
if 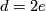 . In the torsion summand we have
. In the torsion summand we have 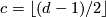 .
.
6 Further discussion
- ...
7 References
- [Macko&Wegner2010] Template:Macko&Wegner2010
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003
|
This page has not been refereed. The information given here might be incomplete or provisional. |