Embeddings in Euclidean space: an introduction to their classification
| Line 1: | Line 1: | ||
| − | == Introduction | + | == Introduction == |
<wikitex>; | <wikitex>; | ||
| Line 11: | Line 11: | ||
classification results for [[embeddings]] of $closed$ $connected$ | classification results for [[embeddings]] of $closed$ $connected$ | ||
manifolds into Euclidean spaces. | manifolds into Euclidean spaces. | ||
| − | + | This is done in particular for codimension 1 and 2 embeddings. | |
| − | + | ||
| − | + | ||
| − | See more in [[Wikipedia:Knot_theory|knot theory]] | + | (There is an extensive study of codimension 2 embeddings not directly |
| − | + | aiming at complete classification. | |
| − | + | Almost none is said here about that. | |
| − | + | So in the title of this article we only mention embeddings of codimension | |
| − | + | greater than 2. | |
| + | See more in [[Wikipedia:Knot_theory|knot theory]].) | ||
| − | == Notation and conventions | + | In the links below we present constructions of embeddings and invariants. |
| + | For more information see \cite{Skopenkov2006}. | ||
| + | |||
| + | == Notation and conventions for the links below == | ||
| − | For a manifold $N$ let $E^m_D(N)$ or $E^m_{PL}(N)$ denote the set of [[smooth]] or [[ | + | For a manifold $N$ let $E^m_D(N)$ or $E^m_{PL}(N)$ denote the set of [[smooth]] or [[piecewise-linear]] (PL) embeddings $N\to\Rr^m$ up to smooth or PL isotopy. If a category is omitted, then the result holds (or a definition or a construction is given) in both categories. |
| − | All manifolds | + | All manifolds are tacitly assumed to be compact. |
Let $B^n$ be a closed $n$-ball in a closed connected $n$-manifold $N$. | Let $B^n$ be a closed $n$-ball in a closed connected $n$-manifold $N$. | ||
| Line 34: | Line 36: | ||
We omit $\Zz$-coefficients from the notation of (co)homology groups. | We omit $\Zz$-coefficients from the notation of (co)homology groups. | ||
| − | For an embedding $f:N\to\Rr^ | + | For an embedding $f:N\to\Rr^m$ denote by |
* $C_f$ the closure of the complement in $S^m\supset\Rr^m$ to a tubular neighborhood of $f(N)$ and | * $C_f$ the closure of the complement in $S^m\supset\Rr^m$ to a tubular neighborhood of $f(N)$ and | ||
*$\nu_f:\partial C_f\to N$ the restriction of the normal bundle of $f$. | *$\nu_f:\partial C_f\to N$ the restriction of the normal bundle of $f$. | ||
</wikitex> | </wikitex> | ||
| − | == Links to specific results == | + | == Links to specific results and examples == |
<wikitex>; | <wikitex>; | ||
| − | [[Hudson tori|Hudson tori]] | + | |
| + | [[Hudson tori|Example of Hudson tori]] | ||
| + | |||
| + | [[Links, i.e. embeddings of non-connected manifolds]] | ||
| + | |||
| + | [[Embeddings of manifolds with boundary]] | ||
| + | |||
</wikitex> | </wikitex> | ||
| Line 47: | Line 55: | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | |||
| − | |||
[[Category:Manifolds]] | [[Category:Manifolds]] | ||
{{Stub}} | {{Stub}} | ||
Revision as of 13:48, 14 February 2010
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
1 Introduction
According to Zeeman, the classical problems of topology are the following.
-
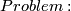 When are two given spaces homeomorphic?
When are two given spaces homeomorphic?
-
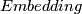
 When does a given space embed into
When does a given space embed into  ?
?
-
 When are two given embeddings isotopic?
When are two given embeddings isotopic?
This article concerns the Knotting Problem.
We recall all known 
 isotopy
classification results for embeddings of
isotopy
classification results for embeddings of 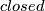
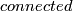 manifolds into Euclidean spaces.
This is done in particular for codimension 1 and 2 embeddings.
manifolds into Euclidean spaces.
This is done in particular for codimension 1 and 2 embeddings.
(There is an extensive study of codimension 2 embeddings not directly aiming at complete classification. Almost none is said here about that. So in the title of this article we only mention embeddings of codimension greater than 2. See more in knot theory.)
In the links below we present constructions of embeddings and invariants. For more information see [Skopenkov2006].
Notation and conventions for the links below
For a manifold  let
let 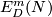 or
or 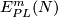 denote the set of smooth or piecewise-linear (PL) embeddings
denote the set of smooth or piecewise-linear (PL) embeddings 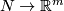 up to smooth or PL isotopy. If a category is omitted, then the result holds (or a definition or a construction is given) in both categories.
up to smooth or PL isotopy. If a category is omitted, then the result holds (or a definition or a construction is given) in both categories.
All manifolds are tacitly assumed to be compact.
Let  be a closed
be a closed  -ball in a closed connected
-ball in a closed connected  -manifold
-manifold  .
Denote
.
Denote 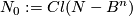 .
.
Let 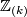 be
be  for
for  even and
even and  for
for  odd.
odd.
We omit  -coefficients from the notation of (co)homology groups.
-coefficients from the notation of (co)homology groups.
For an embedding  denote by
denote by
-
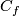 the closure of the complement in
the closure of the complement in 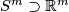 to a tubular neighborhood of
to a tubular neighborhood of 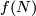 and
and
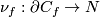 the restriction of the normal bundle of
the restriction of the normal bundle of  .
.
2 Links to specific results and examples
Links, i.e. embeddings of non-connected manifolds
Embeddings of manifolds with boundary
3 References
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
|
This page has not been refereed. The information given here might be incomplete or provisional. |