Embedding
(Created page with "{{Authors|Ulrich Koschorke}} ==Definition== <wikitex>; We work in a fixed category CAT of topological, piecewise linear, $ C^r$--differentiable $(1 \leq r \leq \infty )$ or r...") |
Askopenkov (Talk | contribs) (→Classification) |
||
| (12 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
{{Authors|Ulrich Koschorke}} | {{Authors|Ulrich Koschorke}} | ||
| − | ==Definition== | + | == Definition == |
<wikitex>; | <wikitex>; | ||
| − | We work in a fixed category CAT of topological, piecewise linear, $ C^r$ | + | We work in a fixed category CAT of topological, piecewise linear, $ C^r$-differentiable $(1 \leq r \leq \infty )$ or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them. |
Let $ f : M^m \rightarrow N^n $ be such a map between manifolds of the indicated dimensions $ 1 \leq m < n $. | Let $ f : M^m \rightarrow N^n $ be such a map between manifolds of the indicated dimensions $ 1 \leq m < n $. | ||
| Line 11: | Line 11: | ||
It follows that an embedding cannot have selfintersections. But even an injective immersion need not be an embedding; e. g. the figure six 6<!-- FIXME figure 6 --> | It follows that an embedding cannot have selfintersections. But even an injective immersion need not be an embedding; e. g. the figure six 6<!-- FIXME figure 6 --> | ||
| − | is the image of a smooth immersion but not of an embedding. Note that in the topological and piecewise linear categories,CAT = TOP or PL, our definition yields ''locally flat'' embeddings. In these categories there are other concepts of embeddings - e.g. wild embeddings - which are not locally flat: the condition | + | is the image of a smooth immersion but not of an embedding. Note that in the topological and piecewise linear categories, CAT = TOP or PL, our definition yields ''locally flat'' embeddings. In these categories there are other concepts of embeddings - e.g. wild embeddings - which are not locally flat: the condition |
| − | of local flatness is implied by our definition of immersion. Embeddings (and immersions) into familiar target manifolds such as $\R^n$ may help to visualize abstractly defined manifolds. E. g. all smooth surfaces can be immersed into $\R^3$; but | + | of local flatness is implied by our definition of immersion. Embeddings (and immersions) into familiar target manifolds such as $\R^n$ may help to visualize abstractly defined manifolds. E. g. all [[2-manifolds|smooth surfaces]] can be immersed into $\R^3$; but [[2-manifolds#Non-orientable_surfaces|non-orientable surfaces]] (such as the projective plane and the Klein bottle) allow no embeddings into $\R^3$. |
</wikitex> | </wikitex> | ||
| + | |||
==Existence of embeddings== | ==Existence of embeddings== | ||
<wikitex>; | <wikitex>; | ||
| Line 30: | Line 31: | ||
{{beginrem|Remark}} | {{beginrem|Remark}} | ||
| − | For | + | For more modern expositions see also \cite{Adachi1993|p. 67ff} and \cite{Prasolov2007|22.1}. |
{{endrem}} | {{endrem}} | ||
Similar existence results for embeddings $ M^m \hookrightarrow \R^N $ are valid also in the categories of real analytic maps and of isometrics (Nash) when $ N \gg 2m $ is sufficiently high. | Similar existence results for embeddings $ M^m \hookrightarrow \R^N $ are valid also in the categories of real analytic maps and of isometrics (Nash) when $ N \gg 2m $ is sufficiently high. | ||
</wikitex> | </wikitex> | ||
| + | |||
==Classification== | ==Classification== | ||
<wikitex>; | <wikitex>; | ||
| − | In order to get a survey of all ``essentially distinct´´ embeddings $ f : M \hookrightarrow N $ it is meaningful to introduce equivalence relations such as (ambient) isotopy, concordance, bordism etc., and to aim at classifying embeddings accordingly. Already for the most basic choices of $M$ and $N$ this may turn out to be a very difficult task. E.g. in the [[Wikipedia:Knot theory|theory of knots]] (or links) where $M$ is a sphere (or a finite union of spheres) and $N = \R^ | + | In order to get a survey of all ``essentially distinct´´ embeddings $ f : M \hookrightarrow N $ it is meaningful to introduce equivalence relations such as [[Isotopy|(ambient) isotopy, concordance, bordism]] etc., and to aim at classifying embeddings accordingly. The difficulty of this task depends heavily on the choices of $M$ and $N$ and especially their dimensions: for more information please see the page on [[Embeddings in Euclidean space: an introduction to their classification|high codimension embeddings]]. Already for the most basic choices of $M$ and $N$ this may turn out to be a very difficult task. E.g. in the [[Wikipedia:Knot theory|theory of knots]] (or links) where $M$ is a $1$-sphere (or a finite union of $1$-spheres), and $N = \R^{3}$ the multitude of possible knotting and linking phenomena is just overwhelming. Even classifying links up to the very crude equivalence relation `link homotopy´ is very far from having been achieved yet. |
</wikitex> | </wikitex> | ||
| + | |||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| + | == External links == | ||
| + | * The Wikipedia page about [[Wikipedia:Embedding#Differential_topology|embeddings]] | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
| + | [[Category:Embeddings of manifolds]] | ||
Latest revision as of 09:56, 15 March 2019
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:03, 16 May 2013 and the changes since publication. |
|
The user responsible for this page is Ulrich Koschorke. No other user may edit this page at present. |
Contents |
1 Definition
We work in a fixed category CAT of topological, piecewise linear, 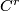 -differentiable
-differentiable 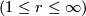 or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them.
or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them.
Let 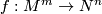 be such a map between manifolds of the indicated dimensions
be such a map between manifolds of the indicated dimensions 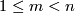 .
.
Definition 1.1.
We call  an embedding (and we write
an embedding (and we write 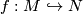 ) if
) if  is an immersion which maps
is an immersion which maps  homeomorphically onto its image.
homeomorphically onto its image.
It follows that an embedding cannot have selfintersections. But even an injective immersion need not be an embedding; e. g. the figure six 6
is the image of a smooth immersion but not of an embedding. Note that in the topological and piecewise linear categories, CAT = TOP or PL, our definition yields locally flat embeddings. In these categories there are other concepts of embeddings - e.g. wild embeddings - which are not locally flat: the condition
of local flatness is implied by our definition of immersion. Embeddings (and immersions) into familiar target manifolds such as 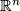 may help to visualize abstractly defined manifolds. E. g. all smooth surfaces can be immersed into
may help to visualize abstractly defined manifolds. E. g. all smooth surfaces can be immersed into 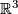 ; but non-orientable surfaces (such as the projective plane and the Klein bottle) allow no embeddings into
; but non-orientable surfaces (such as the projective plane and the Klein bottle) allow no embeddings into 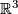 .
.
2 Existence of embeddings
Theorem 2.1 [Penrose&Whitehead&Zeeman1961].
For every compact  --dimensional PL-manifold
--dimensional PL-manifold  there exists a PL--embedding
there exists a PL--embedding 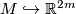 .
.
Remark 2.2. For a good exposition of Theorem 2.1 see also [Rourke&Sanderson1972a, p. 63].
Theorem 2.3 [Whitney1944].
For every closed m--dimensional 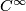 --manifold
--manifold  there exists a
there exists a 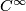 --embedding
--embedding 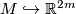 .
.
Remark 2.4. For more modern expositions see also [Adachi1993, p. 67ff] and [Prasolov2007, 22.1].
Similar existence results for embeddings 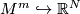 are valid also in the categories of real analytic maps and of isometrics (Nash) when
are valid also in the categories of real analytic maps and of isometrics (Nash) when 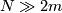 is sufficiently high.
is sufficiently high.
3 Classification
In order to get a survey of all ``essentially distinct´´ embeddings 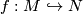 it is meaningful to introduce equivalence relations such as (ambient) isotopy, concordance, bordism etc., and to aim at classifying embeddings accordingly. The difficulty of this task depends heavily on the choices of
it is meaningful to introduce equivalence relations such as (ambient) isotopy, concordance, bordism etc., and to aim at classifying embeddings accordingly. The difficulty of this task depends heavily on the choices of  and
and  and especially their dimensions: for more information please see the page on high codimension embeddings. Already for the most basic choices of
and especially their dimensions: for more information please see the page on high codimension embeddings. Already for the most basic choices of  and
and  this may turn out to be a very difficult task. E.g. in the theory of knots (or links) where
this may turn out to be a very difficult task. E.g. in the theory of knots (or links) where  is a
is a  -sphere (or a finite union of
-sphere (or a finite union of  -spheres), and
-spheres), and 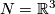 the multitude of possible knotting and linking phenomena is just overwhelming. Even classifying links up to the very crude equivalence relation `link homotopy´ is very far from having been achieved yet.
the multitude of possible knotting and linking phenomena is just overwhelming. Even classifying links up to the very crude equivalence relation `link homotopy´ is very far from having been achieved yet.
4 References
- [Adachi1993] M. Adachi, Embeddings and immersions, Translated from the Japanese by Kiki Hudson. Translations of Mathematical Monographs, 124. Providence, RI: American Mathematical Society (AMS), 1993. MR1225100 (95a:57039) Zbl 0810.57001
- [Penrose&Whitehead&Zeeman1961] R. Penrose, J. Whitehead and E. Zeeman, Imbedding of manifolds in Euclidean space., Ann. of Math. 73 (1961) 613–623. MR0124909 (23 #A2218) Zbl 0113.38101
- [Prasolov2007] V. V. Prasolov, Elements of homology theory, American Mathematical Society, 2007. MR2313004 (2008d:55001) Zbl 1120.55001
- [Rourke&Sanderson1972a] C. P. Rourke and B. J. Sanderson, Introduction to piecewise-linear topology, Springer-Verlag, 1972. MR0350744 (50 #3236) Zbl 0477.57003
- [Whitney1944] H. Whitney, The self-intersections of a smooth
 -manifold in
-manifold in  -space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237
-space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237
5 External links
- The Wikipedia page about embeddings