Covariant derivative
m (→Definition) |
|||
| Line 5: | Line 5: | ||
and $\Gamma E$ the space of smooth sections. A {\it covariant derivative} | and $\Gamma E$ the space of smooth sections. A {\it covariant derivative} | ||
on $E$ is a bilinear map $\nabla : \Gamma TM \times \Gamma E \to \Gamma E$, $(X,s)\mapsto\nabla_Xs$, | on $E$ is a bilinear map $\nabla : \Gamma TM \times \Gamma E \to \Gamma E$, $(X,s)\mapsto\nabla_Xs$, | ||
| − | which is a [[tensor]] (linear over $C^\infty(M)$) in the first argument and | + | which is a [[Tensor|tensor]] (linear over $C^\infty(M)$) in the first argument and |
a {\it derivation} in the second argument: | a {\it derivation} in the second argument: | ||
{{equation|$\begin{matrix}\nabla_{(fX)}s &=& f\nabla_Xs\, \\ \nabla_{X}(fs) &=& (Xf)s + f\nabla_Xs \,,\end{matrix}$|1}} | {{equation|$\begin{matrix}\nabla_{(fX)}s &=& f\nabla_Xs\, \\ \nabla_{X}(fs) &=& (Xf)s + f\nabla_Xs \,,\end{matrix}$|1}} | ||
Revision as of 11:55, 15 March 2013
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
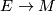 be a vector bundle over a smooth manifold
be a vector bundle over a smooth manifold Tex syntax error
and 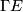 the space of smooth sections. A {\it covariant derivative}
on
the space of smooth sections. A {\it covariant derivative}
on  is a bilinear map
is a bilinear map 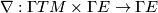 ,
, 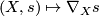 ,
which is a tensor (linear over
,
which is a tensor (linear over 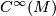 ) in the first argument and
a {\it derivation} in the second argument:
) in the first argument and
a {\it derivation} in the second argument:
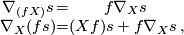 (1)
(1) is a smooth function and
is a smooth function and  a vector field on
a vector field on Tex syntax errorand
 a section of
a section of  , and where
, and where
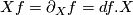 is the ordinary derivative of the function
is the ordinary derivative of the function  in the direction of
in the direction of  . By these
properties,
. By these
properties,  is defined locally and even pointwise regarding the first argument: For any
is defined locally and even pointwise regarding the first argument: For any 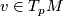 we may define
we may define 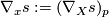 where
where  is any (local) vector field with
is any (local) vector field with 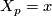 .
.
A covariant derivative has all properties of the ordinary directional derivative
for functions with exception of the commutativity: For functions  we have
we have 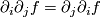 with
with 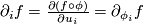 , where
, where 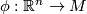 is
is
Tex syntax errorand
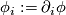
its  -th partial derivative. Instead, for covariant derivatives, the commutator
-th partial derivative. Instead, for covariant derivatives, the commutator
![[\nabla_i,\nabla_j]](/images/math/a/a/4/aa465354fd9efac294989bb1ef5bac3d.png) (with
(with 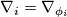 ) is nonzero in general, but it is
only a tensor (rather than a differential operator), the curvature tensor.
) is nonzero in general, but it is
only a tensor (rather than a differential operator), the curvature tensor.
Covariant derivatives are not tensors since they are derivations in the second argument, but
two covariant derivative 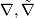 on
on  differ by a tensor:
differ by a tensor:
 defines a tensor
defines a tensor 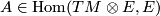 .
.