Covariant derivative
m (→Definition) |
|||
| Line 26: | Line 26: | ||
</wikitex> | </wikitex> | ||
| − | == References == | + | == References== |
{{#RefList:}} | {{#RefList:}} | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
Revision as of 11:37, 15 March 2013
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let 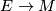 be a vector bundle over a smooth manifold
be a vector bundle over a smooth manifold  and
and 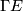 the space of smooth sections. A {\it covariant derivative}
on
the space of smooth sections. A {\it covariant derivative}
on  is a bilinear map
is a bilinear map 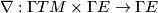 ,
, 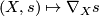 ,
which is a tensor (linear over
,
which is a tensor (linear over 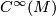 ) in the first argument and
a {\it derivation} in the second argument:
) in the first argument and
a {\it derivation} in the second argument:
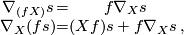 (1)
(1)where  is a smooth function and
is a smooth function and  a vector field on
a vector field on  and
and  a section of
a section of  , and where
, and where
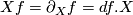 is the ordinary derivative of the function
is the ordinary derivative of the function  in the direction of
in the direction of  . By these
properties,
. By these
properties,  is defined locally and even pointwise regarding the first argument: For any
is defined locally and even pointwise regarding the first argument: For any 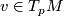 we may define
we may define 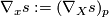 where
where  is any (local) vector field with
is any (local) vector field with 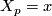 .
.
A covariant derivative has all properties of the ordinary directional derivative
for functions with exception of the commutativity: For functions  we have
we have 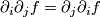 with
with 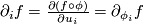 , where
, where 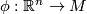 is
a local parametrization of
is
a local parametrization of  and
and 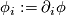 its
its  -th partial derivative. Instead, for covariant derivatives, the commutator
-th partial derivative. Instead, for covariant derivatives, the commutator
![[\nabla_i,\nabla_j]](/images/math/a/a/4/aa465354fd9efac294989bb1ef5bac3d.png) (with
(with 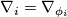 ) is nonzero in general, but it is
only a tensor (rather than a differential operator), the curvature tensor.
) is nonzero in general, but it is
only a tensor (rather than a differential operator), the curvature tensor.
Covariant derivatives are not tensors since they are derivations in the second argument, but
two covariant derivative 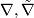 on
on  differ by a tensor:
differ by a tensor:
 defines a tensor
defines a tensor 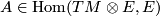 .
.