Bundle structures and lifting problems (Ex)
(Created page with "<wikitex>; Given a (pointed) map $g:Y\to Z$ of pointed topological space, we define the homotopy fiber as\footnote{Here $PZ$ is the space of paths starting at the base-point ...") |
m |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Given a (pointed) map $g:Y\to Z$ of pointed topological space, we define the homotopy fiber as\footnote{Here | + | == Lifting maps == |
| + | Given a (pointed) map $g: Y\to Z$ of pointed topological space, we define the homotopy fiber as\footnote{Here | ||
$PZ$ is the space of paths starting at the base-point of $Z$.} | $PZ$ is the space of paths starting at the base-point of $Z$.} | ||
$$ | $$ | ||
\mathrm{hofib}(g):=\{(y,\gamma)\in Y\times PZ|\,\gamma(1)=g(y),\,\gamma(0)=z_0\} | \mathrm{hofib}(g):=\{(y,\gamma)\in Y\times PZ|\,\gamma(1)=g(y),\,\gamma(0)=z_0\} | ||
$$ | $$ | ||
| − | and we denote by $p$: $\ | + | and we denote by $p$: $\text{hofib}(g)\to Y$ the projection. |
| − | + | {{beginthm|Exercise}} | |
| − | + | Prove the following: | |
| − | + | ||
| − | + | A map $f:X \to Y$ of pointed space has a lift $\bar f:X\to \text{hofib}(g)$ along $p$ if and only if $g\circ f$ is homotopic to the constant map. | |
| + | {{endthm}} | ||
| + | {{beginrem|Hint}} This is a special case of \cite{Hatcher2002|Proposition 4.72}. | ||
| + | {{endrem}} | ||
| − | + | == Classification of orientations and spin structures on vector bundles == | |
Recall the Definition of Eilenberg-MacLane-spaces. | Recall the Definition of Eilenberg-MacLane-spaces. | ||
| − | + | We denote the space of pointed loops in a space $X$ by $\Omega X$. | |
| − | + | {{beginthm|Exercise}} | |
| − | + | * Show: There is a homotopy equivalence $\Omega K(n+1,\bbz/2\bbz)\simeq K(n,\bbz/2\bbz)$.\\ | |
| − | + | ||
| + | '''Hint''': Use the uniqueness of Eilenberg-MacLane-spaces and the long exact sequence in homotopy | ||
associated to the path-space-fibration | associated to the path-space-fibration | ||
$$\Omega K(n+1,\bbz/2\bbz)\to P(K(n+1,\bbz/2\bbz))\to K(n+1,\bbz/2\bbz) \;.$$ | $$\Omega K(n+1,\bbz/2\bbz)\to P(K(n+1,\bbz/2\bbz))\to K(n+1,\bbz/2\bbz) \;.$$ | ||
Recall that the path-space is contractible. | Recall that the path-space is contractible. | ||
| − | + | * Show that the set of homotopy classes of pointed maps $[Y,\Omega X]$ has a group structure | |
| − | induced by composition of paths. | + | induced by composition of paths. |
| − | + | ||
| − | + | ||
| + | '''Hint''': This is similar to the group structure of the fundamental group. | ||
| − | + | Maybe you've heard that the group $H^1(X,\Zz/2\Zz)$ acts free and transitively on the set | |
| − | Maybe you've heard that the group $H^1(X,\ | + | |
of spin structures of an oriented vector bundle $\xi\to X$ (X a compact pointed space). | of spin structures of an oriented vector bundle $\xi\to X$ (X a compact pointed space). | ||
| − | Now recall that\ | + | Now recall that \ref{The group structure on $H^1(X,\bbz/2\bbz)$ is due to the Exercise 3.2.} |
| − | $H^1(X,\bbz/2\bbz)\cong [X,K(1,\bbz/2\bbz)]$, | + | $H^1(X,\bbz/2\bbz)\cong [X,K(1,\bbz/2\bbz)]$, where $K(1,\bbz/2\bbz)$ denotes an Eilenberg-MacLane-space. |
| − | where $K(1,\bbz/2\bbz)$ denotes an Eilenberg-MacLane-space | + | |
| − | + | ||
| − | + | ||
So we first prove the statement about classification of spin structures. | So we first prove the statement about classification of spin structures. | ||
The warm-up is the classification of orientations: | The warm-up is the classification of orientations: | ||
| − | + | # The first Stiefel-Whitney class is a map $w_1:BO\to K(1,\bbz/2\bbz)$. | |
| − | + | # The homotopy fiber hofib($w_1$) is $BSO$. | |
| − | + | # The projection $p:BSO\to BO$ is the map induced by $SO\hookrightarrow O$. | |
| − | + | ||
| − | + | Assume that the homotopy groups of $O$ are known. | |
| − | + | # Calculate the homotopy groups of $BO$ using the fibration $0\to EO\to BO$. | |
| − | + | # Calculate the homotopy groups of $BSO$ using the fibration $$BSO\to BO\to K(1,\bbz/2\bbz)\;.$$ | |
| − | + | # Calculate the homotopy fibre of $p:BSO\to BO$. | |
| − | + | ||
| − | + | ||
| − | + | ||
Now we can classify the orientations on a vector bundle $\xi\to X$. | Now we can classify the orientations on a vector bundle $\xi\to X$. | ||
For this we need to know that the sequence | For this we need to know that the sequence | ||
| − | $$\ | + | $$\text{hofib}(p)\to BSO \to BO$$ |
fits into the following diagram\footnote{It's non-trivial | fits into the following diagram\footnote{It's non-trivial | ||
to see that the functor $B$ can be applied to each of those spaces.}: | to see that the functor $B$ can be applied to each of those spaces.}: | ||
| − | + | ||
| − | + | Hence there are group structures on $[X,\text{hofib}(p)]$ and $[X,BSO]$ (the latter one is the Whitney-sum of vector bundles). Furthermore there is an action of $[X,\text{hofib}(p)]$ on $[X,BSO]$ induced by $q$. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Hence there are group structures on $[X,\ | + | |
| − | of vector bundles). Furthermore there is an action of $[X,\ | + | |
| − | by $q$. | + | |
{{beginthm|Definition}} | {{beginthm|Definition}} | ||
Revision as of 20:38, 28 March 2012
1 Lifting maps
Given a (pointed) map 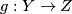 of pointed topological space, we define the homotopy fiber as\footnote{Here
of pointed topological space, we define the homotopy fiber as\footnote{Here
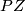 is the space of paths starting at the base-point of
is the space of paths starting at the base-point of 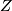 .}
.}
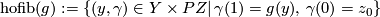
and we denote by  :
: 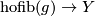 the projection.
the projection.
Exercise 2.1. Prove the following:
A map 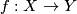 of pointed space has a lift
of pointed space has a lift 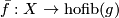 along
along  if and only if
if and only if 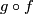 is homotopic to the constant map.
is homotopic to the constant map.
Hint 2.2. This is a special case of [Hatcher2002, Proposition 4.72].
2 Classification of orientations and spin structures on vector bundles
Recall the Definition of Eilenberg-MacLane-spaces.
We denote the space of pointed loops in a space  by
by 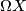 .
.
Exercise 4.1.
- Show: There is a homotopy equivalence
Tex syntax error
.\\
Hint: Use the uniqueness of Eilenberg-MacLane-spaces and the long exact sequence in homotopy
associated to the path-space-fibration
Tex syntax error
Recall that the path-space is contractible.
- Show that the set of homotopy classes of pointed maps
![[Y,\Omega X]](/images/math/3/d/3/3d36331b6ffc21a47fc28e20effd0b46.png) has a group structure
has a group structure
induced by composition of paths.
Hint: This is similar to the group structure of the fundamental group.
Maybe you've heard that the group 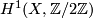 acts free and transitively on the set
of spin structures of an oriented vector bundle
acts free and transitively on the set
of spin structures of an oriented vector bundle 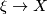 (X a compact pointed space).
(X a compact pointed space).
Tex syntax erroris due to the Exercise 3.2.}
Tex syntax error, where
Tex syntax errordenotes an Eilenberg-MacLane-space.
So we first prove the statement about classification of spin structures. The warm-up is the classification of orientations:
- The first Stiefel-Whitney class is a map
Tex syntax error
. - The homotopy fiber hofib(
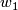 ) is
) is 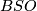 .
.
- The projection
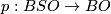 is the map induced by
is the map induced by 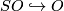 .
.
Assume that the homotopy groups of 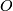 are known.
are known.
- Calculate the homotopy groups of
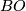 using the fibration
using the fibration 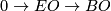 .
.
- Calculate the homotopy groups of
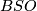 using the fibration
using the fibration Tex syntax error
- Calculate the homotopy fibre of
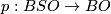 .
.
Now we can classify the orientations on a vector bundle 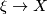 .
For this we need to know that the sequence
.
For this we need to know that the sequence
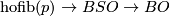
fits into the following diagram\footnote{It's non-trivial
to see that the functor  can be applied to each of those spaces.}:
can be applied to each of those spaces.}:
Hence there are group structures on ![[X,\text{hofib}(p)]](/images/math/9/7/8/978bcfb0ba0034c61359e401a84462d3.png) and
and ![[X,BSO]](/images/math/9/9/9/999c116c9d83c1d788b2710e4a033b65.png) (the latter one is the Whitney-sum of vector bundles). Furthermore there is an action of
(the latter one is the Whitney-sum of vector bundles). Furthermore there is an action of ![[X,\text{hofib}(p)]](/images/math/9/7/8/978bcfb0ba0034c61359e401a84462d3.png) on
on ![[X,BSO]](/images/math/9/9/9/999c116c9d83c1d788b2710e4a033b65.png) induced by
induced by  .
.
Definition 4.2.
A vector bundle is called \underline{orientable} if its classifying map 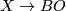 lifts along
lifts along 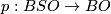 . An orientation is the choice of such a lift.
. An orientation is the choice of such a lift.
Let  denote a compact pointed space and
denote a compact pointed space and 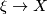 a vector bundle on
a vector bundle on  .
.
- Use Exercise 3.1 to show that
 is orientable if and only if its first Stiefel-Whitney class
is orientable if and only if its first Stiefel-Whitney class
vanishes.
- Show that the group
Tex syntax error
acts free and transitively on the set of
homotopy classes of lifts. Hint: Use the homotopy-lifting property and Exercise 3.1
- Given an interpretation of the group
Tex syntax error
.
Now there are similar results for spin structures (on oriented vector bundles).
Exercise 4.3.
Repeat Exercises 3.3 and 3.4 using the second Stiefel-Whitney class 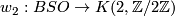 . The homotopy fibre of
. The homotopy fibre of 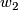 is BSpin, where Spin is the colimit over
is BSpin, where Spin is the colimit over 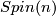 , the universal covers of
, the universal covers of 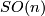 .
.
References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
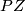 is the space of paths starting at the base-point of
is the space of paths starting at the base-point of 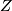 .}
.}
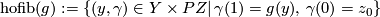
and we denote by  :
: 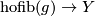 the projection.
the projection.
Exercise 2.1. Prove the following:
A map 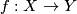 of pointed space has a lift
of pointed space has a lift 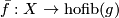 along
along  if and only if
if and only if 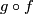 is homotopic to the constant map.
is homotopic to the constant map.
Hint 2.2. This is a special case of [Hatcher2002, Proposition 4.72].
2 Classification of orientations and spin structures on vector bundles
Recall the Definition of Eilenberg-MacLane-spaces.
We denote the space of pointed loops in a space  by
by 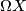 .
.
Exercise 4.1.
- Show: There is a homotopy equivalence
Tex syntax error
.\\
Hint: Use the uniqueness of Eilenberg-MacLane-spaces and the long exact sequence in homotopy
associated to the path-space-fibration
Tex syntax error
Recall that the path-space is contractible.
- Show that the set of homotopy classes of pointed maps
![[Y,\Omega X]](/images/math/3/d/3/3d36331b6ffc21a47fc28e20effd0b46.png) has a group structure
has a group structure
induced by composition of paths.
Hint: This is similar to the group structure of the fundamental group.
Maybe you've heard that the group 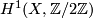 acts free and transitively on the set
of spin structures of an oriented vector bundle
acts free and transitively on the set
of spin structures of an oriented vector bundle 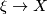 (X a compact pointed space).
(X a compact pointed space).
Tex syntax erroris due to the Exercise 3.2.}
Tex syntax error, where
Tex syntax errordenotes an Eilenberg-MacLane-space.
So we first prove the statement about classification of spin structures. The warm-up is the classification of orientations:
- The first Stiefel-Whitney class is a map
Tex syntax error
. - The homotopy fiber hofib(
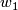 ) is
) is 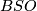 .
.
- The projection
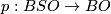 is the map induced by
is the map induced by 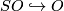 .
.
Assume that the homotopy groups of 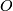 are known.
are known.
- Calculate the homotopy groups of
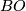 using the fibration
using the fibration 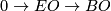 .
.
- Calculate the homotopy groups of
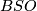 using the fibration
using the fibration Tex syntax error
- Calculate the homotopy fibre of
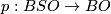 .
.
Now we can classify the orientations on a vector bundle 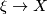 .
For this we need to know that the sequence
.
For this we need to know that the sequence
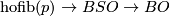
fits into the following diagram\footnote{It's non-trivial
to see that the functor  can be applied to each of those spaces.}:
can be applied to each of those spaces.}:
Hence there are group structures on ![[X,\text{hofib}(p)]](/images/math/9/7/8/978bcfb0ba0034c61359e401a84462d3.png) and
and ![[X,BSO]](/images/math/9/9/9/999c116c9d83c1d788b2710e4a033b65.png) (the latter one is the Whitney-sum of vector bundles). Furthermore there is an action of
(the latter one is the Whitney-sum of vector bundles). Furthermore there is an action of ![[X,\text{hofib}(p)]](/images/math/9/7/8/978bcfb0ba0034c61359e401a84462d3.png) on
on ![[X,BSO]](/images/math/9/9/9/999c116c9d83c1d788b2710e4a033b65.png) induced by
induced by  .
.
Definition 4.2.
A vector bundle is called \underline{orientable} if its classifying map 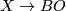 lifts along
lifts along 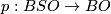 . An orientation is the choice of such a lift.
. An orientation is the choice of such a lift.
Let  denote a compact pointed space and
denote a compact pointed space and 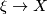 a vector bundle on
a vector bundle on  .
.
- Use Exercise 3.1 to show that
 is orientable if and only if its first Stiefel-Whitney class
is orientable if and only if its first Stiefel-Whitney class
vanishes.
- Show that the group
Tex syntax error
acts free and transitively on the set of
homotopy classes of lifts. Hint: Use the homotopy-lifting property and Exercise 3.1
- Given an interpretation of the group
Tex syntax error
.
Now there are similar results for spin structures (on oriented vector bundles).
Exercise 4.3.
Repeat Exercises 3.3 and 3.4 using the second Stiefel-Whitney class 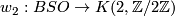 . The homotopy fibre of
. The homotopy fibre of 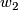 is BSpin, where Spin is the colimit over
is BSpin, where Spin is the colimit over 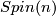 , the universal covers of
, the universal covers of 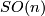 .
.
References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001