Bonn THDM 2013: Program
m (→K0 and Wall's finiteness obstruction) |
m |
||
| Line 8: | Line 8: | ||
Speaker: [[User:Lueck|WL]] | Speaker: [[User:Lueck|WL]] | ||
| − | We introduce the ''projective class group $K_0(R)$''. We explain computations for | + | Abstract: We introduce the ''projective class group $K_0(R)$''. We explain computations for |
special rings, e.g., fields, complex group rings for finite groups. We state Swan's | special rings, e.g., fields, complex group rings for finite groups. We state Swan's | ||
Theorem which relate the projective class group of the ring $C(X)$ of continuous | Theorem which relate the projective class group of the ring $C(X)$ of continuous | ||
| Line 25: | Line 25: | ||
Speaker: [[User:Lueck|WL]] | Speaker: [[User:Lueck|WL]] | ||
| − | We introduce $K_1(R)$ and the Whitehead group $\textup{Wh}(G)$. | + | Abstract: We introduce $K_1(R)$ and the Whitehead group $\textup{Wh}(G)$. |
We define the Whitehead torsion of a homotopy equivalence of finite connected $CW$-complexes. | We define the Whitehead torsion of a homotopy equivalence of finite connected $CW$-complexes. | ||
We discuss the algebraic and topological significance of these notions, in particular the $s$-cobordism theorem. We briefly introduce the surgery program. | We discuss the algebraic and topological significance of these notions, in particular the $s$-cobordism theorem. We briefly introduce the surgery program. | ||
| Line 93: | Line 93: | ||
Speaker :[[User:Lueck|WL]] | Speaker :[[User:Lueck|WL]] | ||
| − | We introduce spectra and how they yield homology theories. | + | Abstract: We introduce spectra and how they yield homology theories. |
We state the Farrell-Jones Conjecture and the Baum-Connes Conjecture | We state the Farrell-Jones Conjecture and the Baum-Connes Conjecture | ||
for torsion free groups and discuss applications of these conjectures, such as the | for torsion free groups and discuss applications of these conjectures, such as the | ||
| Line 103: | Line 103: | ||
Speaker: [[User:Lueck|WL]] | Speaker: [[User:Lueck|WL]] | ||
| − | We introduce classifying spaces for families. | + | Abstract: We introduce classifying spaces for families. |
We define equivariant homology theories and explain how they can be construced by spectra over groupoids. | We define equivariant homology theories and explain how they can be construced by spectra over groupoids. | ||
Then we state the Farrell-Jones Conjecture and the Baum-Connes Conjecture in general. | Then we state the Farrell-Jones Conjecture and the Baum-Connes Conjecture in general. | ||
| Line 112: | Line 112: | ||
Speaker: [[User:Lueck|WL]] | Speaker: [[User:Lueck|WL]] | ||
| − | We give a status report of the Farrell-Jones Conjecture, | + | Abstract: We give a status report of the Farrell-Jones Conjecture, |
discuss open cases and the search for potential counterexamples, and briefly | discuss open cases and the search for potential counterexamples, and briefly | ||
survey the methods of proof. | survey the methods of proof. | ||
Revision as of 14:42, 19 July 2013
Contents |
1 Introduction
1.1 K0 and Wall's finiteness obstruction
Speaker: WL
Abstract: We introduce the projective class group 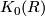 . We explain computations for
special rings, e.g., fields, complex group rings for finite groups. We state Swan's
Theorem which relate the projective class group of the ring
. We explain computations for
special rings, e.g., fields, complex group rings for finite groups. We state Swan's
Theorem which relate the projective class group of the ring 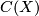 of continuous
of continuous
 -valued functions to the Grothendieck group of vector bundles over
-valued functions to the Grothendieck group of vector bundles over  , if
, if  is a
finite
is a
finite  -complex. We discuss Wall's finiteness obstruction that decides whether a finitely
dominated
-complex. We discuss Wall's finiteness obstruction that decides whether a finitely
dominated  -complex is homotopy equivalent to a finite
-complex is homotopy equivalent to a finite  -complex and takes values in
the projective class group of the integral group ring of the fundamental group.
-complex and takes values in
the projective class group of the integral group ring of the fundamental group.
Exercises: K-group, zeroth (Ex), Finitely dominated CW complexes (Ex).
References: [Lück1987], [Lück1989], [Mislin1995], [Ranicki1985], [Rosenberg1994], [Wall1965a], [Wall1966b].
1.2 K1 and Whitehead torsion
Speaker: WL
Abstract: We introduce 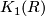 and the Whitehead group
and the Whitehead group 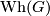 .
We define the Whitehead torsion of a homotopy equivalence of finite connected
.
We define the Whitehead torsion of a homotopy equivalence of finite connected  -complexes.
We discuss the algebraic and topological significance of these notions, in particular the
-complexes.
We discuss the algebraic and topological significance of these notions, in particular the  -cobordism theorem. We briefly introduce the surgery program.
Finally we introduce negative
-cobordism theorem. We briefly introduce the surgery program.
Finally we introduce negative  -theory and the Bass-Heller-Swan decomposition.
-theory and the Bass-Heller-Swan decomposition.
1.3 Normal maps and surgery below the middle dimension
1.4 L-groups
1.5 Surgery in the middle dimension
1.6 The geometric surgery exact sequence
2 Surgery on smooth manifolds
2.1 Homotopy spheres and other examples
2.2 Smoothing and surgery
2.3 Classifying spaces for surgery
2.4 The Kervaire invariant in surgery
3 Algebraic L-theory
3.1 L-groups via chain complexes
3.2 Signatures
3.3 L-groups of categories and assembly maps
3.4 Surgery obstructions and assembly maps
4 The isomorphism conjectures
4.1 The Isomorphism Conjectures in the torsion-free case
Speaker :WL
Abstract: We introduce spectra and how they yield homology theories. We state the Farrell-Jones Conjecture and the Baum-Connes Conjecture for torsion free groups and discuss applications of these conjectures, such as the Kaplansky Conjecture and the Borel Conjecture. We explain that the formulations for torsion free groups cannot extend to arbitrary groups.
4.2 The Isomorphism Conjectures in general
Speaker: WL
Abstract: We introduce classifying spaces for families. We define equivariant homology theories and explain how they can be construced by spectra over groupoids. Then we state the Farrell-Jones Conjecture and the Baum-Connes Conjecture in general. We discuss further applications, such as the Novikov Conjecture.
4.3 Status and methods of proof;
Speaker: WL
Abstract: We give a status report of the Farrell-Jones Conjecture, discuss open cases and the search for potential counterexamples, and briefly survey the methods of proof.
5 References
- [Lück1987] W. Lück, The geometric finiteness obstruction, Proc. London Math. Soc. (3) 54 (1987), no.2, 367–384. MR872812 (88i:57007) Zbl 0626.57011
- [Lück1989] W. Lück, Transformation groups and algebraic
 -theory, LNM, 1408, Springer-Verlag, 1989. MR1027600 (91g:57036) Zbl 0709.57024
-theory, LNM, 1408, Springer-Verlag, 1989. MR1027600 (91g:57036) Zbl 0709.57024
- [Mislin1995] G. Mislin, Wall's finiteness obstruction, Handbook of algebraic topology, North-Holland, Amsterdam, (1995), 1259–1291. MR1361911 (97g:57029) Zbl 0870.57030
- [Ranicki1985] A. Ranicki, The algebraic theory of finiteness obstruction, Math. Scand. 57 (1985), no.1, 105–126. MR815431 (87d:18014) Zbl 0589.57018
- [Rosenberg1994] J. Rosenberg, Algebraic
 -theory and its applications, Graduate Texts in Mathematics, 147, Springer-Verlag, 1994. MR1282290 (95e:19001) Zbl 0801.19001
-theory and its applications, Graduate Texts in Mathematics, 147, Springer-Verlag, 1994. MR1282290 (95e:19001) Zbl 0801.19001
- [Wall1965a] C. T. C. Wall, Finiteness conditions for
 -complexes, Ann. of Math. (2) 81 (1965), 56–69. MR0171284 (30 #1515) Zbl 0152.21902
-complexes, Ann. of Math. (2) 81 (1965), 56–69. MR0171284 (30 #1515) Zbl 0152.21902
- [Wall1966b] C. T. C. Wall, Finiteness conditions for
 complexes. II, Proc. Roy. Soc. Ser. A 295 (1966), 129–139. MR0211402 (35 #2283)Zbl 0152.21902
complexes. II, Proc. Roy. Soc. Ser. A 295 (1966), 129–139. MR0211402 (35 #2283)Zbl 0152.21902