B-Bordism
| Line 4: | Line 4: | ||
On this page we recall the definition of the bordism groups of closed manifolds, with extra topological structure: orientation, spin-structure, weak complex structure etc. The ideas here date back to {{cite|Lashof1965}}. There is a deatiled treatment in {{cite|Stong1968|Chapter II}} and a summary in {{cite|Kreck1999|Section 1}} as well as {{cite|Kreck&Lück2005|18.10}}. | On this page we recall the definition of the bordism groups of closed manifolds, with extra topological structure: orientation, spin-structure, weak complex structure etc. The ideas here date back to {{cite|Lashof1965}}. There is a deatiled treatment in {{cite|Stong1968|Chapter II}} and a summary in {{cite|Kreck1999|Section 1}} as well as {{cite|Kreck&Lück2005|18.10}}. | ||
| − | We specify extra topological structure universally by means of a fibration $\ | + | We specify extra topological structure universally by means of a fibration $\gamma : B \to BO$ where $BO$ denotes the classifying space of the stable orthogonal group and $B$ is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes $B$ for the fibraion $\gamma$. A $B$-manifold is a compact manifold $M$ together with a lift of a classifying map for the stable normal bundle of $M$ to $B$: |
$$ | $$ | ||
\xymatrix{ | \xymatrix{ | ||
& B \ar[d]^{\gamma} \\ | & B \ar[d]^{\gamma} \\ | ||
| − | W \ar[r]_{\nu_W}\ar[ur]^{\bar \nu} & BO.} | + | W \ar[r]_{\nu_W} \ar[ur]^{\bar \nu} & BO.} |
$$ | $$ | ||
The n-dimensional $B$-bordism group is defined to be the set of closed $B$-manifolds up modulo the relation of $B$-bordism and addition given by disjoint union | The n-dimensional $B$-bordism group is defined to be the set of closed $B$-manifolds up modulo the relation of $B$-bordism and addition given by disjoint union | ||
| − | $$ \Omega_n^B := \{ | + | $$ \Omega_n^B := \{ (M, \bar \nu) \}/\simeq.$$ |
Alternative notations are $\Omega_n(B)$ and also $\Omega_n^G$ when $B \to BO = BG \to BO$ for $G \to O$ a stable represenation of a topological group $G$. Details of the definition and some important theorems for computing $\Omega_n^B$ follow. | Alternative notations are $\Omega_n(B)$ and also $\Omega_n^G$ when $B \to BO = BG \to BO$ for $G \to O$ a stable represenation of a topological group $G$. Details of the definition and some important theorems for computing $\Omega_n^B$ follow. | ||
| Line 18: | Line 18: | ||
== B-structures == | == B-structures == | ||
<wikitex>; | <wikitex>; | ||
| − | Let $G_{r, m}$ denote the Grassman manifold of unoriented r-planes in $\Rr^n$ and let $BO(r) = lim_{m \to \infty} G_{r, m}$ be the infinite Grassman and fix a fibration $\ | + | In this section we give a compressed accont of {{cite|Stong1968|Chapter II}}. Let $G_{r, m}$ denote the Grassman manifold of unoriented r-planes in $\Rr^n$ and let $BO(r) = lim_{m \to \infty} G_{r, m}$ be the infinite Grassman and fix a fibration $\gamma_r : B_r \to BO(r)$. |
| + | |||
{{beginthm|Definition}} | {{beginthm|Definition}} | ||
| − | Let $\xi: E \to X$ be a rank r vector bundle classified by $\xi : X \to BO(r)$. A $B_r$-structure on $\xi$ is a vertical homotopy class of maps $\bar \xi : X \to B_r$ such that $\ | + | Let $\xi: E \to X$ be a rank r vector bundle classified by $\xi : X \to BO(r)$. A $B_r$-structure on $\xi$ is a vertical homotopy class of maps $\bar \xi : X \to B_r$ such that $\gamma_r \circ \bar \xi = \xi$. |
{{endthm}} | {{endthm}} | ||
| − | |||
| + | Note that if $\xi_0$ and $\xi_1$ are isomorphic vector bundles over $X$ then the sets of $B_r$-structures on each are in bijective equivalence. However $B_r$-structures are defined on specific bundles, not isomorphism classes of bundles: an specific isomorphism, up to appropriate equivalence, is required to give a map between the set of $B_r$ structures. Happily this is the case for the normal bundle as we now explain. | ||
| − | + | Let $M$ be a compact manifold and let $i_0 : M \to \Rr^{n+r}$ be an embedding. Equipping $\Rr^{n+r}$ with the standard metric, the normal bundle of $i_0$ is a rank r vector bundle over classified by its normal Gauss map $\nu(i_0) : M \to G_{r, n+r} \subset BO(r)$. If $i_1$ is another such embedding and $r >> n$, then $i_1$ is regularly homotopic to $i_0$ and all regular homotopies are regularly homotopic relative to their endpoints. A regular homotopy $H$ defines an isomorphism $\alpha_H :\nu(i_0) \cong \nu(i_1)$ and a regular homotopy of regular homotopies gives a homotopy between these isomorphisms. Taking care one proves the following | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {{beginthm|Lemma|{{cite|Stong1968|p 15}}}} | |
| − | + | For r sufficiently large, (depending only on n) there is a 1-1 correspondence between the $B_r$ structures of the normal bundles of any two embeddings $i_0, i_1 : M \to \Rr^{n+r}$. | |
| − | + | {{endthm}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Now let $(B_r, \gamma_r)$ be a sequence of fibrations over $BO(r)$ with maps $g_r : B_r \to B_{r+1}$ fitting into the following commutative diagram | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
$$ | $$ | ||
| − | \xymatrix{ | + | \xymatrix{ |
| − | + | B_r \ar[r]^{g_r} \ar[d]^{\gamma_r} & B_{r+1} \ar[d]^{\gamma_{r+1}} \\ | |
| − | + | BO(r) \ar[r]^{j_r} & BO(r+1) | |
| + | } | ||
$$ | $$ | ||
| − | A $B$-manifold is a pair $( | + | where $j_r$ is the standard inclusion and let $B = lim_{r \to \infty}(B_r)$. A $B_r$-structure on the normal bundle of an embedding $i: M \to \Rr^{n+r}$ defines a unique $B_{r+1}$-structure on the composition of $i$ with the standard inclusion $\Rr^{n+r} \to \Rr^{n+r+1}$. |
| + | |||
| + | {{beginthm|Defition}} | ||
| + | A $B$-structure on $M$ is an equivalence class of $B_r$-structure on $M$ where two such structures are equivalent if they become equivalent for r sufficiently large. A $B$-manifold is a pair $(M, \bar \nu)$ where $M$ is a compact manifold and $\bar \nu$ is a $B$-structure on $M$. | ||
| + | {{endthm}} | ||
| + | |||
| + | If $W$ is a compact manifold with boundary $\partial W$ then by choosing the inward-pointing normal vector along $\partial W$, a $B$-structure on $W$ restricts to a $B$-structure on $\partial W$. In particular, if $(M, \bar \nu_M)$ is a closed $B$ manifold then $W = M \times [0, 1]$ has a canonical $B$-structure $\bar \nu_{M \times [0, 1]}$ such that restricting to $(M, \bar \nu_M)$ on $M \times \{ 0 \}$. The restriction of this $B$-structure to $M \times \{ 1 \}$ is denoted $-\bar \nu$: by construction $(M \sqcup M, \bar \nu \sqcup - \bar \nu)$ is the boundary of $(M \times [0, 1], \bar \nu_{M \times [0, 1]}$. | ||
| + | |||
| + | {{beginthm|Definition}} | ||
| + | Closed $B$-manifolds $(M_0, \bar \nu_0)$ and $(M_1, \bar \nu_1)$ are $B$-bordant if there is a compact $B$-manifold $(W, \bar \nu)$ such that $\partial(W, \bar \nu) = (M_0 \sqcup M_1, \bar \nu_0 \sqcup -\bar \nu_1)$. We write $[M, \bar \nu]$ for the bordism class of $(M, \bar \nu)$. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Proposition}} | ||
| + | The set of $B$-borism class of closed n-manifolds with $B$-structure, | ||
| + | $$ \Omega_n^B := \{ [M, \bar \nu ] \},$$ | ||
| + | forms an abelian group under the operation of disjoint union with inverse $-[M,\bar \nu] = [M, -\bar \nu]$. | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
== The Pontrjagin Thom isomorphism == | == The Pontrjagin Thom isomorphism == | ||
| − | <wikitex> | + | <wikitex>; |
| − | $$ \Omega_n^B \cong \pi_n^S(MB)$$ | + | If $E$ is a vector bundle, let $T(E)$ denote its Thom space. Recall that $B = (B_r, \gamma_r, g_r)$ is a sequence of fibrations $\gamma_r : B_r \to BO(r)$ with compatible maps $g_r : B_r \to B_{r+1}$. These data give rise to a stable vector bundle as defined in {{cite|Kreck&Lück2005|18.10}} with $E_r \to B_r$ equal to the pullback bundle $\gamma_r^*(EO(r))$ where $EO(r)$. This stable vector bundle defines a Thom spectrum which we denote $MB$. The r-th space of $MB$ is $T(E_r)$. |
| + | |||
| + | By definition a $B$-manifold $(M, \bar \nu)$ is an equivalence class of $B_r$ structures on $\nu(i)$, the normal bundle of an embedding $i : M \to \Rr^{n+r}$. Hence $(M, \bar \nu)$ gives rise to the collapse map $S^{n+r} \to T(E_r)$ where identify $S^{n+r}$ with the one-point compatificiation of $\Rr^{n+r}$, we map via $\bar \nu_r$ on a tubular neighbourhood of $i(M) \subset \Rr^{n+r}$ and we map all other points to the base-point of $T(E_r)$. As r increase these maps are compatibly related by suspension and the structure maps of the spectrum $MB$. Hence we obtain a homotopy class $PT((M, \bar \mu)) \in lim_{r \to \infty}(\pi_{n+r}(T(E_r)) = \pi_n(MB)$. The celebrated theorem of Pontrjagin and Thom states in part that $PT(M, \bar \nu)$ depends only on the bordism class $[M, \bar]$. | ||
| + | {{beginthm|Theorem}} | ||
| + | There is an isomorphism of abelian groups | ||
| + | $$ PT : \Omega_n^B \cong \pi_n^S(MB), ~~~[M, \bar \nu] \longmapsto PT([M, \bar \nu]).$$ | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
== Spectral sequences == | == Spectral sequences == | ||
| − | <wikitex> | + | <wikitex>; |
$$ H_p(B; \pi_q^S) \Longrightarrow \Omega_{p+q}^B$$ | $$ H_p(B; \pi_q^S) \Longrightarrow \Omega_{p+q}^B$$ | ||
</wikitex> | </wikitex> | ||
Revision as of 18:58, 21 January 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
On this page we recall the definition of the bordism groups of closed manifolds, with extra topological structure: orientation, spin-structure, weak complex structure etc. The ideas here date back to [Lashof1965]. There is a deatiled treatment in [Stong1968, Chapter II] and a summary in [Kreck1999, Section 1] as well as [Kreck&Lück2005, 18.10].
We specify extra topological structure universally by means of a fibration 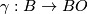 where
where 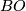 denotes the classifying space of the stable orthogonal group and
denotes the classifying space of the stable orthogonal group and  is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes
is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes  for the fibraion
for the fibraion 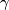 . A
. A  -manifold is a compact manifold
-manifold is a compact manifold  together with a lift of a classifying map for the stable normal bundle of
together with a lift of a classifying map for the stable normal bundle of  to
to  :
:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ W \ar[r]_{\nu_W} \ar[ur]^{\bar \nu} & BO.}](/images/math/4/8/0/4801d251719f7177254c076b305ed742.png)
The n-dimensional  -bordism group is defined to be the set of closed
-bordism group is defined to be the set of closed  -manifolds up modulo the relation of
-manifolds up modulo the relation of  -bordism and addition given by disjoint union
-bordism and addition given by disjoint union
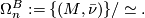
Alternative notations are 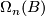 and also
and also 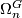 when
when 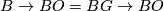 for
for 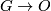 a stable represenation of a topological group
a stable represenation of a topological group  . Details of the definition and some important theorems for computing
. Details of the definition and some important theorems for computing 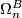 follow.
follow.
2 B-structures
In this section we give a compressed accont of [Stong1968, Chapter II]. Let 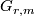 denote the Grassman manifold of unoriented r-planes in
denote the Grassman manifold of unoriented r-planes in  and let
and let 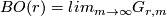 be the infinite Grassman and fix a fibration
be the infinite Grassman and fix a fibration 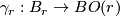 .
.
Definition 2.1.
Let 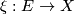 be a rank r vector bundle classified by
be a rank r vector bundle classified by 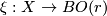 . A
. A  -structure on
-structure on  is a vertical homotopy class of maps
is a vertical homotopy class of maps 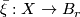 such that
such that 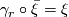 .
.
Note that if 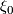 and
and 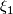 are isomorphic vector bundles over
are isomorphic vector bundles over  then the sets of
then the sets of  -structures on each are in bijective equivalence. However
-structures on each are in bijective equivalence. However  -structures are defined on specific bundles, not isomorphism classes of bundles: an specific isomorphism, up to appropriate equivalence, is required to give a map between the set of
-structures are defined on specific bundles, not isomorphism classes of bundles: an specific isomorphism, up to appropriate equivalence, is required to give a map between the set of  structures. Happily this is the case for the normal bundle as we now explain.
structures. Happily this is the case for the normal bundle as we now explain.
Let  be a compact manifold and let
be a compact manifold and let 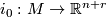 be an embedding. Equipping
be an embedding. Equipping 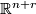 with the standard metric, the normal bundle of
with the standard metric, the normal bundle of 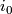 is a rank r vector bundle over classified by its normal Gauss map
is a rank r vector bundle over classified by its normal Gauss map 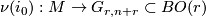 . If
. If 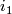 is another such embedding and
is another such embedding and 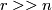 , then
, then 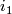 is regularly homotopic to
is regularly homotopic to 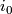 and all regular homotopies are regularly homotopic relative to their endpoints. A regular homotopy
and all regular homotopies are regularly homotopic relative to their endpoints. A regular homotopy  defines an isomorphism
defines an isomorphism 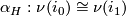 and a regular homotopy of regular homotopies gives a homotopy between these isomorphisms. Taking care one proves the following
and a regular homotopy of regular homotopies gives a homotopy between these isomorphisms. Taking care one proves the following
Lemma 2.2 [Stong1968, p 15].
For r sufficiently large, (depending only on n) there is a 1-1 correspondence between the  structures of the normal bundles of any two embeddings
structures of the normal bundles of any two embeddings 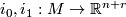 .
.
Now let 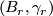 be a sequence of fibrations over
be a sequence of fibrations over 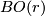 with maps
with maps 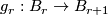 fitting into the following commutative diagram
fitting into the following commutative diagram
![\displaystyle \xymatrix{ B_r \ar[r]^{g_r} \ar[d]^{\gamma_r} & B_{r+1} \ar[d]^{\gamma_{r+1}} \\ BO(r) \ar[r]^{j_r} & BO(r+1) }](/images/math/7/c/1/7c1c615ec7ae50c39e222dd0f32582ad.png)
where 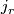 is the standard inclusion and let
is the standard inclusion and let 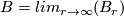 . A
. A  -structure on the normal bundle of an embedding
-structure on the normal bundle of an embedding 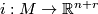 defines a unique
defines a unique 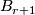 -structure on the composition of
-structure on the composition of  with the standard inclusion
with the standard inclusion 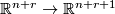 .
.
Defition 2.3.
A  -structure on
-structure on  is an equivalence class of
is an equivalence class of  -structure on
-structure on  where two such structures are equivalent if they become equivalent for r sufficiently large. A
where two such structures are equivalent if they become equivalent for r sufficiently large. A  -manifold is a pair
-manifold is a pair 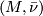 where
where  is a compact manifold and
is a compact manifold and 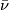 is a
is a  -structure on
-structure on  .
.
If  is a compact manifold with boundary
is a compact manifold with boundary 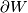 then by choosing the inward-pointing normal vector along
then by choosing the inward-pointing normal vector along 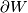 , a
, a  -structure on
-structure on  restricts to a
restricts to a  -structure on
-structure on 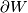 . In particular, if
. In particular, if 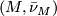 is a closed
is a closed  manifold then
manifold then ![W = M \times [0, 1]](/images/math/3/d/8/3d810ac2ba6ec7b778512bb115c679a1.png) has a canonical
has a canonical  -structure
-structure ![\bar \nu_{M \times [0, 1]}](/images/math/d/5/e/d5e27b479782bc34079dd44364fbde46.png) such that restricting to
such that restricting to 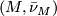 on
on 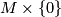 . The restriction of this
. The restriction of this  -structure to
-structure to 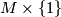 is denoted
is denoted 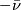 : by construction
: by construction 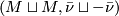 is the boundary of
is the boundary of ![(M \times [0, 1], \bar \nu_{M \times [0, 1]}](/images/math/a/9/d/a9d3fb32fb0598cf9671c752ba48d552.png) .
.
Definition 2.4.
Closed  -manifolds
-manifolds 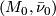 and
and 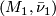 are
are  -bordant if there is a compact
-bordant if there is a compact  -manifold
-manifold 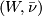 such that
such that 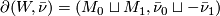 . We write
. We write ![[M, \bar \nu]](/images/math/3/0/2/30282bb5acfadbc45b3b2f90df238541.png) for the bordism class of
for the bordism class of 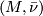 .
.
Proposition 2.5.
The set of  -borism class of closed n-manifolds with
-borism class of closed n-manifolds with  -structure,
-structure,
![\displaystyle \Omega_n^B := \{ [M, \bar \nu ] \},](/images/math/0/e/c/0ec9d94e5d00beba3be787adfd09d089.png)
forms an abelian group under the operation of disjoint union with inverse ![-[M,\bar \nu] = [M, -\bar \nu]](/images/math/4/5/0/450ad56098e90f7f2f6b0b2b9e710fd2.png) .
.
3 The Pontrjagin Thom isomorphism
If  is a vector bundle, let
is a vector bundle, let 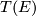 denote its Thom space. Recall that
denote its Thom space. Recall that 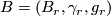 is a sequence of fibrations
is a sequence of fibrations 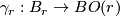 with compatible maps
with compatible maps 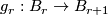 . These data give rise to a stable vector bundle as defined in [Kreck&Lück2005, 18.10] with
. These data give rise to a stable vector bundle as defined in [Kreck&Lück2005, 18.10] with 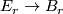 equal to the pullback bundle
equal to the pullback bundle 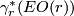 where
where 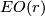 . This stable vector bundle defines a Thom spectrum which we denote
. This stable vector bundle defines a Thom spectrum which we denote 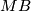 . The r-th space of
. The r-th space of 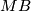 is
is 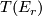 .
.
By definition a  -manifold
-manifold 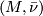 is an equivalence class of
is an equivalence class of  structures on
structures on 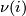 , the normal bundle of an embedding
, the normal bundle of an embedding 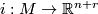 . Hence
. Hence 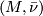 gives rise to the collapse map
gives rise to the collapse map 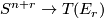 where identify
where identify 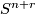 with the one-point compatificiation of
with the one-point compatificiation of 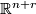 , we map via
, we map via 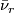 on a tubular neighbourhood of
on a tubular neighbourhood of 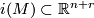 and we map all other points to the base-point of
and we map all other points to the base-point of 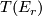 . As r increase these maps are compatibly related by suspension and the structure maps of the spectrum
. As r increase these maps are compatibly related by suspension and the structure maps of the spectrum 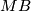 . Hence we obtain a homotopy class
. Hence we obtain a homotopy class 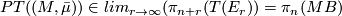 . The celebrated theorem of Pontrjagin and Thom states in part that
. The celebrated theorem of Pontrjagin and Thom states in part that 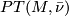 depends only on the bordism class
depends only on the bordism class ![[M, \bar]](/images/math/6/8/9/68959df2c8dd6dffc2566b3f8843159a.png) .
.
Theorem 3.1. There is an isomorphism of abelian groups
![\displaystyle PT : \Omega_n^B \cong \pi_n^S(MB), ~~~[M, \bar \nu] \longmapsto PT([M, \bar \nu]).](/images/math/b/e/4/be440f446b0b509c12f36b28487f5a89.png)
4 Spectral sequences
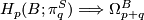
5 References
- [Kreck&Lück2005] M. Kreck and W. Lück, The Novikov conjecture, Birkhäuser Verlag, Basel, 2005. MR2117411 (2005i:19003) Zbl 1058.19001
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Lashof1965] R. Lashof, Problems in differential and algebraic topology. Seattle Conference, 1963, Ann. of Math. (2) 81 (1965), 565–591. MR0182961 (32 #443) Zbl 0137.17601
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010