B-Bordism
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
On this page we recall the definition of the bordism groups of closed manifolds, with extra topological structure: orientation, spin-structure, weak complex structure etc. The ideas here date back to [Lashof1965]. There is a deatiled treatment in [Stong1968, Chapter II] and a summary in [Kreck1999, Section 1] as well as [Kreck&Lück2005, 18.10].
We specify extra topological structure universally by means of a fibration 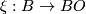 where
where 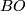 denotes the classifying space of the stable orthogonal group and
denotes the classifying space of the stable orthogonal group and  is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes
is homotopy equivalent to a CW complex of finite type. Abusing notation, one writes  for the fibraion
for the fibraion  . A
. A  -manifold is a compact manifold
-manifold is a compact manifold  together with a lift of a classifying map for the stable normal bundle of
together with a lift of a classifying map for the stable normal bundle of  to
to  :
:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ W \ar[r]_{\nu_W}\ar[ur]^{\bar \nu} & BO.}](/images/math/c/2/5/c25a11f4d9ccd5c2e076d6d5ea3e9ec9.png)
The n-dimensional  -bordism group is defined to be the set of closed
-bordism group is defined to be the set of closed  -manifolds up modulo the relation of
-manifolds up modulo the relation of  -bordism and addition given by disjoint union
-bordism and addition given by disjoint union
![\displaystyle \Omega_n^B := \{ [M, \bar \nu] \}/\simeq .](/images/math/0/1/5/01509fee91d5f3f2dd65573e15d9e729.png)
Alternative notations are 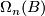 and also
and also 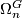 when
when 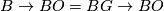 for
for 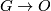 a stable represenation of a topological group
a stable represenation of a topological group  . Details of the definition and some important theorems for computing
. Details of the definition and some important theorems for computing 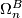 follow.
follow.
2 B-structures
Let 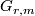 denote the Grassman manifold of unoriented r-planes in
denote the Grassman manifold of unoriented r-planes in 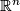 and let
and let 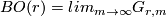 be the infinite Grassman and fix a fibration
be the infinite Grassman and fix a fibration 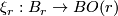 .
.
Definition 2.1.
Let 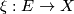 be a rank r vector bundle classified by
be a rank r vector bundle classified by 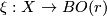 . A
. A 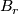 -structure on
-structure on  is a vertical homotopy class of maps
is a vertical homotopy class of maps 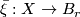 such that
such that 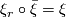 .
.
3 Stable vector bundles
We recall the defintion of a stable vector bundle from [Kreck&Lück2005, 18.10] which requires some notation. Let 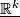 denote the trivial rank k bundle
denote the trivial rank k bundle 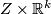 : the space
: the space 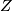 will be clear from context. Let
will be clear from context. Let 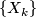 be a sequence
be a sequence 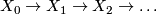 of inclusions
of inclusions 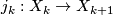 of CW-complexes. A stable vector bundle
of CW-complexes. A stable vector bundle  over
over 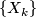 is a sequence of rank k-vector bundles
is a sequence of rank k-vector bundles 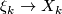 and a sequence of bundle maps
and a sequence of bundle maps
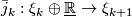
where 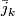 covers the inclusion
covers the inclusion 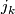 . An isomorphism of stable vector bundles over
. An isomorphism of stable vector bundles over 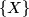 ,
, 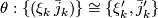 is a sequence of bundle ismorphisms
is a sequence of bundle ismorphisms 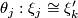 for
for 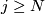 ,
,  some integer, which are compatible with
some integer, which are compatible with 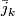 and
and 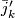 .
.
Here are some important examples:
- A rank
 -vector
-vector 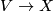 over a CW complex
over a CW complex  defines a stable vector bundle
defines a stable vector bundle 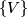 by setting
by setting 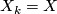 fixed for all
fixed for all  ,
, 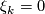 for
for 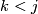 and
and 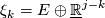 for
for 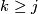 with
with 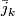 the obvious inclusions.
the obvious inclusions.
- If
 is a compact n-manifold then
is a compact n-manifold then  embedds into
embedds into 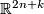 for
for 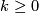 and for
and for 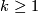 two such embeddings are isotopic. The normal bundle of any such embedding defines a stable vector bundle over
two such embeddings are isotopic. The normal bundle of any such embedding defines a stable vector bundle over  as in the first example and there is a canonical isomorphicm between any two such stable bundles given by isotopies between the embeddings. We write
as in the first example and there is a canonical isomorphicm between any two such stable bundles given by isotopies between the embeddings. We write 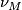 for the stable normal bundle of
for the stable normal bundle of  . Note that by defintion
. Note that by defintion 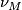 is a stable inverse to the tangent bundle of
is a stable inverse to the tangent bundle of  :
:
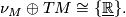
- The universal bundle
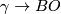 is the stable bundle with
is the stable bundle with 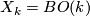 ,
, 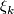 the universal
the universal  -plane bundle and
-plane bundle and 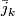 the classifymap of
the classifymap of 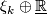 .
.
- If
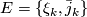 is a stable vector bundle over
is a stable vector bundle over 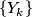 and
and  is a sequence of maps
is a sequence of maps 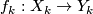 compatible with inclusions then
compatible with inclusions then 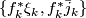 is a stable vector bundle over
is a stable vector bundle over 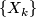 called the pull-back bundle and denoted
called the pull-back bundle and denoted 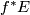 .
.
4 B-manifolds and B-bordism
Let 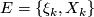 be a stable vector bundle. A normal
be a stable vector bundle. A normal  -manifold is a triple
-manifold is a triple 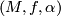 consisting of a compact manifold
consisting of a compact manifold  , a sequence of maps
, a sequence of maps 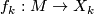 , and a stable bundle isomorphism
, and a stable bundle isomorphism 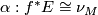 .
.
Recall that 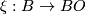 is a fibration. We next define normal
is a fibration. We next define normal  -manifolds and normal
-manifolds and normal  -bordism: more details are given in [Stong1968][Chapter II] and [Kreck1999][Section 1]. If
-bordism: more details are given in [Stong1968][Chapter II] and [Kreck1999][Section 1]. If  is a compact smooth manifold then
is a compact smooth manifold then 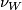 is classified by a map, also denoted
is classified by a map, also denoted 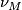 ,
, 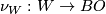 :
: 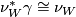 . A
. A  -structure on
-structure on  is a map
is a map 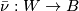 lifting
lifting 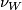 through
through  :
:
![\displaystyle \xymatrix{ & B \ar[d]^{\gamma} \\ W \ar[r]_{\nu_W}\ar[ur]^{\bar \nu} & BO.}](/images/math/c/2/5/c25a11f4d9ccd5c2e076d6d5ea3e9ec9.png)
A  -manifold is a pair
-manifold is a pair 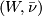 where
where 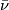 is a
is a  -structure on
-structure on  . If
. If  has boundary
has boundary 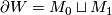 , a disjoint union of two closed
, a disjoint union of two closed  -manifolds with inclusions
-manifolds with inclusions 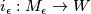 ,
, 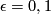 , then
, then  is a
is a  -bordism between the
-bordism between the  -manifolds
-manifolds 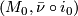 and
and 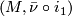 .
.
5 The Pontrjagin Thom isomorphism
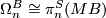
6 Spectral sequences
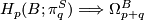
7 References
- [Kreck&Lück2005] M. Kreck and W. Lück, The Novikov conjecture, Birkhäuser Verlag, Basel, 2005. MR2117411 (2005i:19003) Zbl 1058.19001
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Lashof1965] R. Lashof, Problems in differential and algebraic topology. Seattle Conference, 1963, Ann. of Math. (2) 81 (1965), 565–591. MR0182961 (32 #443) Zbl 0137.17601
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010