6-manifolds: 2-connected
m (→Mapping class groups) |
m |
||
| Line 24: | Line 24: | ||
* the third Betti-number of $M$ is given by $b_3(M) = 2b$, | * the third Betti-number of $M$ is given by $b_3(M) = 2b$, | ||
* the Euler characteristic of $M$ is given by $\chi(M) = 2 - 2b$, | * the Euler characteristic of $M$ is given by $\chi(M) = 2 - 2b$, | ||
| − | * the [[Intersection | + | * the [[Intersection form|intersection form]] of $M$ is isomorphic to the sum of b-copies of $H_{-}(\Zz)$, the standard [[Intersection form#Skew-symmetric bilinear forms|skew-symmetric hyperbolic]] form on $\Zz^2$. |
</wikitex> | </wikitex> | ||
Revision as of 15:57, 19 April 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Tex syntax errorbe the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds
 (the notation is used to be consistent with 6-manifolds: 1-connected).
The classification
(the notation is used to be consistent with 6-manifolds: 1-connected).
The classification Tex syntax errorwas one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The is a precise 6-dimensional analogue of the classification of orientable surfaces: every 2-connected 6-manifold
 is diffeomorphic to a connected-sum
is diffeomorphic to a connected-sum
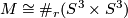
where by definition 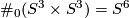 and in general
and in general  is determined by the formula for the Euler characteristic of
is determined by the formula for the Euler characteristic of 
Tex syntax error
Tex syntax error, see 6-manifolds: 1-connected.
2 Construction and examples
The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
-
Tex syntax error
, the standard 6-sphere. -
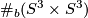 , the
, the Tex syntax error
-fold connected sum ofTex syntax error
.
3 Invariants
Suppose that  is diffeomorphic to
is diffeomorphic to 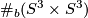 then:
then:
-
Tex syntax error
, - the third Betti-number of
 is given by
is given by Tex syntax error
, - the Euler characteristic of
 is given by
is given by Tex syntax error
, - the intersection form of
 is isomorphic to the sum of b-copies of
is isomorphic to the sum of b-copies of Tex syntax error
, the standard skew-symmetric hyperbolic form onTex syntax error
.
4 Classification
Recall that the following theorem was stated in other words in the introduction:
Theorem 4.1 [Smale1962a, Corolary 1.3].
The semi-group of 2-connected 6-manifolds is generated byTex syntax error.
Tex syntax errordenotes the natural numbers we obtain a bijection
Tex syntax error
5 Further discussion
5.1 Topological 2-connected 6-manifolds
Let 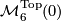 be the set of homeomorphism classes of topological 2-connected 6-manifolds.
be the set of homeomorphism classes of topological 2-connected 6-manifolds.
Theorem 5.1. Every topological 2-connected 6-manifold admits a smooth structure which is unique up to diffoemorphism. In particular, there is a bijection
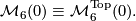
Proof.
For any such manifold we have
we have Tex syntax errorand so
 is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.
is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.

5.2 Mapping class groups
Let 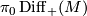 denote the group of isotopy classes of diffeomorphisms
denote the group of isotopy classes of diffeomorphisms 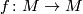 of a
of a  -connected
-connected  -manifold
-manifold  and let
and let 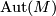 denote the group of isomorphisms of
denote the group of isomorphisms of 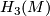 perserving the intersection form:
perserving the intersection form: 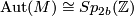 is the symplectic group when
is the symplectic group when 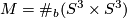 . By [Cerf1970] the forgetful map to the group of orientation preserving pseudo-isotopy classes of
. By [Cerf1970] the forgetful map to the group of orientation preserving pseudo-isotopy classes of  is an isomorphism. Applying Cerf's theorem Kreck proved in [Kreck1979] that there are exact sequences
is an isomorphism. Applying Cerf's theorem Kreck proved in [Kreck1979] that there are exact sequences
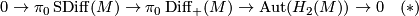
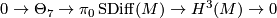
where by definition 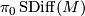 is the subgroup of isotopy classes induced the identity on
is the subgroup of isotopy classes induced the identity on 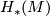 and
and  is the group of homotopy
is the group of homotopy  -spheres.
-spheres.
In particular 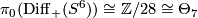 .
.
For more information about the extensions in 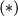 above, see [Krylov2003], [Johnson1983] and [Crowley2009].
above, see [Krylov2003], [Johnson1983] and [Crowley2009].
References
- [Cerf1970] J. Cerf, La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie, Inst. Hautes Études Sci. Publ. Math. (1970), no.39, 5–173. MR0292089 (45 #1176) Zbl 0213.25202
- [Crowley2009] D. Crowley, On the mapping class groups of
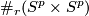 for
for 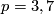 , (2009). Available at the arXiv:0905.0423.
, (2009). Available at the arXiv:0905.0423.
- [Johnson1983] D. Johnson, A survey of the Torelli group, Low-dimensional topology (San Francisco, Calif., 1981), Amer. Math. Soc. (1983), 165–179. MR718141 (85d:57009) Zbl 0553.57002
- [Kreck1979] M. Kreck, Isotopy classes of diffeomorphisms of
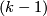 -connected almost-parallelizable
-connected almost-parallelizable 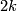 -manifolds, Algebraic topology, Aarhus 1978 (Proc. Sympos., Univ. Aarhus, Aarhus, 1978), Springer (1979), 643–663. MR561244 (81i:57029) Zbl 0421.57009
-manifolds, Algebraic topology, Aarhus 1978 (Proc. Sympos., Univ. Aarhus, Aarhus, 1978), Springer (1979), 643–663. MR561244 (81i:57029) Zbl 0421.57009
- [Krylov2003] N. A. Krylov, On the Jacobi group and the mapping class group of
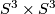 , Trans. Amer. Math. Soc. 355 (2003), no.1, 99–117 (electronic). MR1928079 (2003i:57039) Zbl 1015.57020
, Trans. Amer. Math. Soc. 355 (2003), no.1, 99–117 (electronic). MR1928079 (2003i:57039) Zbl 1015.57020
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103