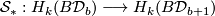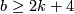6-manifolds: 2-connected
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
Let  be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds
be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds  (the notation is used to be consistent with 6-manifolds: 1-connected).
(the notation is used to be consistent with 6-manifolds: 1-connected).
The classification  was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The is a precise 6-dimensional analogue of the classification of orientable surfaces: every 2-connected 6-manifold
was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The is a precise 6-dimensional analogue of the classification of orientable surfaces: every 2-connected 6-manifold  is diffeomorphic to a connected-sum
is diffeomorphic to a connected-sum
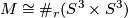
where by definition 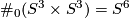 and in general
and in general  is determined by the formula for the Euler characteristic of
is determined by the formula for the Euler characteristic of 
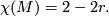
For the more general case where 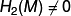 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
[edit] 2 Construction and examples
The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
-
 , the standard 6-sphere.
, the standard 6-sphere.
-
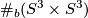 , the
, the  -fold connected sum of
-fold connected sum of 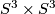 .
.
[edit] 3 Invariants
Suppose that  is diffeomorphic to
is diffeomorphic to 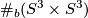 then:
then:
-
 ,
,
- the third Betti-number of
 is given by
is given by 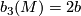 ,
,
- the Euler characteristic of
 is given by
is given by  ,
,
- the intersection form of
 is isomorphic to the sum of b-copies of
is isomorphic to the sum of b-copies of  , the standard skew-symmetric hyperbolic form on
, the standard skew-symmetric hyperbolic form on 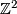 .
.
[edit] 4 Classification
Recall that the following theorem was stated in other words in the introduction:
Theorem 4.1 [Smale1962a, Corolary 1.3].
The semi-group of 2-connected 6-manifolds is generated by 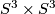 .
.
Hence if  denotes the natural numbers we obtain a bijection
denotes the natural numbers we obtain a bijection
![\displaystyle \mathcal{M}_6(0)\equiv \Nn,~~~[M] \mapsto \frac{1}{2}b_3(M)./var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_U93SKs](/images/math/4/f/8/4f87caab28b3b9b7fd16a5f88c9bb677.png)
[edit] 5 Further discussion
[edit] 5.1 Topological 2-connected 6-manifolds
Let 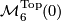 be the set of homeomorphism classes of topological 2-connected 6-manifolds.
be the set of homeomorphism classes of topological 2-connected 6-manifolds.
Theorem 5.1. Every topological 2-connected 6-manifold admits a smooth structure which is unique up to diffoemorphism. In particular, there is a bijection
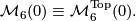
Proof.
For any such manifold  we have
we have 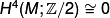 and so
and so  is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.
is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.

[edit] 5.2 Mapping class groups
Let 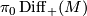 denote the group of isotopy classes of diffeomorphisms
denote the group of isotopy classes of diffeomorphisms 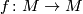 of a
of a  -connected
-connected  -manifold
-manifold  and let
and let 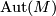 denote the group of isomorphisms of
denote the group of isomorphisms of 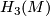 perserving the intersection form:
perserving the intersection form: 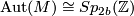 is the symplectic group when
is the symplectic group when 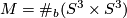 . By [Cerf1970] the forgetful map to the group of orientation preserving pseudo-isotopy classes of
. By [Cerf1970] the forgetful map to the group of orientation preserving pseudo-isotopy classes of  is an isomorphism. Applying Cerf's theorem Kreck proved in [Kreck1979] that there are exact sequences
is an isomorphism. Applying Cerf's theorem Kreck proved in [Kreck1979] that there are exact sequences
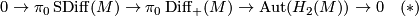
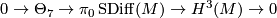
where by definition 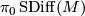 is the subgroup of isotopy classes induced the identity on
is the subgroup of isotopy classes induced the identity on 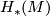 and
and  is the group of homotopy
is the group of homotopy  -spheres.
-spheres.
In particular 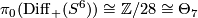 .
.
For more information about the extensions in 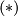 above, see [Krylov2003], [Johnson1983] and [Crowley2009].
above, see [Krylov2003], [Johnson1983] and [Crowley2009].
[edit] 5.3 Diffeomorphism groups
Let 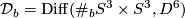 denote group of diffeomorphisms of
denote group of diffeomorphisms of 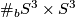 which are the identity inside a marked disc, and
which are the identity inside a marked disc, and 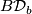 denote the classifying spaces of this topological group. Connect-sum inside the marked disc gives homomorphisms
denote the classifying spaces of this topological group. Connect-sum inside the marked disc gives homomorphisms 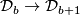 , and so continuous maps
, and so continuous maps 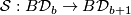 . The homology of these classifying spaces is approachable in a range of degrees, by the following theorem.
. The homology of these classifying spaces is approachable in a range of degrees, by the following theorem.
Let 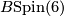 denote the classifying space of the group
denote the classifying space of the group 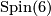 , and
, and 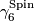 denote its universal vector bundle. We write
denote its universal vector bundle. We write 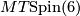 for the Thom spectrum of the virtual bundle
for the Thom spectrum of the virtual bundle 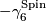 . Pontrjagin--Thom theory provides a map
. Pontrjagin--Thom theory provides a map
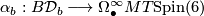
to the basepoint component of the infinite loop space of the spectrum 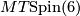 , and these fit together under the maps
, and these fit together under the maps 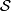 to give a map
to give a map
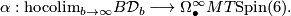
Theorem 5.3 [Galatius&Randal-Williams2012a, Corollary 1.2].
The map  induces an isomorphism on (co)homology.
induces an isomorphism on (co)homology.
It is not difficult to calculate the rational cohomology of 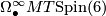 , and find that it is a polynomial algebra with generators in degrees
, and find that it is a polynomial algebra with generators in degrees 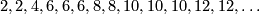 , which can be given an explicit description in terms of generalised Miller-Morita-Mumford classes. By the stability theorem, this calculates the rational cohomology of
, which can be given an explicit description in terms of generalised Miller-Morita-Mumford classes. By the stability theorem, this calculates the rational cohomology of  in degrees
in degrees 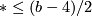 .
.
[edit] 6 References
- [Cerf1970] J. Cerf, La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie, Inst. Hautes Études Sci. Publ. Math. (1970), no.39, 5–173. MR0292089 (45 #1176) Zbl 0213.25202
- [Crowley2009] D. Crowley, On the mapping class groups of
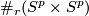 for
for 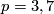 , (2009). Available at the arXiv:0905.0423.
, (2009). Available at the arXiv:0905.0423.
- [Galatius&Randal-Williams2012] S. Galatius and O. Randal-Williams, Homological stability for moduli spaces of high dimensional manifolds, (2012). Available at the arXiv:1203.6830.
- [Galatius&Randal-Williams2012a] S. Galatius and O. Randal-Williams, Stable moduli spaces of high dimensional manifolds, (2012). Available at the arXiv:1201.3527.
- [Johnson1983] D. Johnson, A survey of the Torelli group, Low-dimensional topology (San Francisco, Calif., 1981), Amer. Math. Soc. (1983), 165–179. MR718141 (85d:57009) Zbl 0553.57002
- [Kreck1979] M. Kreck, Isotopy classes of diffeomorphisms of
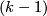 -connected almost-parallelizable
-connected almost-parallelizable 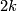 -manifolds, Algebraic topology, Aarhus 1978 (Proc. Sympos., Univ. Aarhus, Aarhus, 1978), Springer (1979), 643–663. MR561244 (81i:57029) Zbl 0421.57009
-manifolds, Algebraic topology, Aarhus 1978 (Proc. Sympos., Univ. Aarhus, Aarhus, 1978), Springer (1979), 643–663. MR561244 (81i:57029) Zbl 0421.57009
- [Krylov2003] N. A. Krylov, On the Jacobi group and the mapping class group of
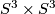 , Trans. Amer. Math. Soc. 355 (2003), no.1, 99–117 (electronic). MR1928079 (2003i:57039) Zbl 1015.57020
, Trans. Amer. Math. Soc. 355 (2003), no.1, 99–117 (electronic). MR1928079 (2003i:57039) Zbl 1015.57020
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103