6-manifolds: 2-connected
(→Invariants) |
(→Topological 2-connected 6-manifolds) |
||
| Line 45: | Line 45: | ||
$$ \mathcal{M}_6(e) \rightarrow \mathcal{M}^{\Top}_6(e).$$ | $$ \mathcal{M}_6(e) \rightarrow \mathcal{M}^{\Top}_6(e).$$ | ||
{{endthm}} | {{endthm}} | ||
| − | + | ||
| + | {{beginproof}} | ||
| + | For any such manifold $M$ we have $H^4(M; \Zz/2) \cong 0$ and so $M$ is smoothable (see [[6-manifolds: 1-connected#Smoothing theory|6-manifolds: 1-connected]]). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem \ref{thm:classification} are diffeomorphic. | ||
| + | {{endproof}} | ||
</wikitex> | </wikitex> | ||
Revision as of 18:12, 10 June 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let  be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds
be the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds  .
.
The classification  was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold
was one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold  is diffeomorphic to a connected-sum
is diffeomorphic to a connected-sum
Tex syntax error
Tex syntax errorand in general
 is determined by the formula for the Euler characteristic of
is determined by the formula for the Euler characteristic of 
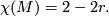
- For the more general case where
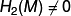 , see 6-manifolds: 1-connected.
, see 6-manifolds: 1-connected.
2 Construction and examples
The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
-
 , the standard 6-sphere.
, the standard 6-sphere.
-
Tex syntax error
, the -fold connected sum of
-fold connected sum of 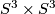 .
.
3 Invariants
 is diffeomorphic to
is diffeomorphic to Tex syntax errorthen:
-
 ,
,
- the third Betti-number of
 is given by
is given by 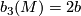 ,
,
- the Euler characteristic of
 is given by
is given by  ,
,
- the intersection form of
 is isomorphic to the sum of b-copies of
is isomorphic to the sum of b-copies of  , the standard skew-symmetric hyperbolic form on
, the standard skew-symmetric hyperbolic form on 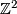 .
.
4 Classification
Recall that the following theorem was stated in other words in the introduction:
Theorem 4.1 [Smale1962a, Corolary 1.3].
The semi-group of 2-connected 6-manifolds is generated by 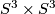 .
.
Hence if  denotes the natural numbers we obtain a bijection
denotes the natural numbers we obtain a bijection
![\displaystyle \mathcal{M}_6(0)\equiv \Nn,~~~[M] \mapsto \frac{1}{2}b_3(M).](/images/math/4/f/8/4f87caab28b3b9b7fd16a5f88c9bb677.png)
5 Further discussion
5.1 Topological 2-connected 6-manifolds
Let 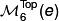 be the set of homeomorphism classes of topological 2-connected 6-manifolds.
be the set of homeomorphism classes of topological 2-connected 6-manifolds.
Theorem 5.1. Every topological 2-connected 6-manifold admits a smooth structure which is unique up to diffoemorphism. That is, there is a bijection
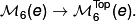
Proof.
For any such manifold  we have
we have 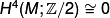 and so
and so  is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.
is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.

5.2 Mapping class groups
...
References
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103