6-manifolds: 2-connected
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Tex syntax errorbe the set of diffeomorphism classes of closed smooth simply-connected 2-connected 6-manifolds
 .
The classification
.
The classification Tex syntax errorwas one of Smale's first applications of the h-cobordism theorem [Smale1962a, Corollary 1.3]. The classification, as for oriented surfaces is strikingly simple: every 2-connected 6-manifold
 is diffeomorphic to a connected-sum
is diffeomorphic to a connected-sum
Tex syntax error
Tex syntax errorand in general
 is determined by the formula for the Euler characteristic of
is determined by the formula for the Euler characteristic of 
Tex syntax error
- For the more general case where
Tex syntax error
, see 6-manifolds: 1-connected.
2 Construction and examples
The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
-
 , the standard 6-sphere.
, the standard 6-sphere.
-
Tex syntax error
, the -fold connected sum of
-fold connected sum of Tex syntax error
.
3 Invariants
 is diffeomorphic to
is diffeomorphic to Tex syntax errorthen:
-
Tex syntax error
, - the third Betti-number of
 is given by
is given by Tex syntax error
, - the Euler characteristic of
 is given by
is given by Tex syntax error
, - the intersection form of
 is isomorphic to the sum of b-copies of
is isomorphic to the sum of b-copies of Tex syntax error
, the standard skew-symmetric hyperbolic form on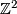 .
.
4 Classification
Recall that the following theorem was stated in other words in the introduction:
Theorem 4.1 [Smale1962a, Corolary 1.3].
The semi-group of 2-connected 6-manifolds is generated byTex syntax error.
Hence if  denotes the natural numbers we obtain a bijection
denotes the natural numbers we obtain a bijection
![\displaystyle \mathcal{M}_6(0)\equiv \Nn,~~~[M] \mapsto \frac{1}{2}b_3(M).](/images/math/4/f/8/4f87caab28b3b9b7fd16a5f88c9bb677.png)
5 Further discussion
5.1 Topological 2-connected 6-manifolds
Let 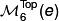 be the set of homeomorphism classes of topological 2-connected 6-manifolds.
be the set of homeomorphism classes of topological 2-connected 6-manifolds.
Theorem 5.1. Every topological 2-connected 6-manifold admits a smooth structure which is unique up to diffoemorphism. That is, there is a bijection
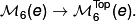
Proof.
For any such manifold  we have
we have 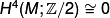 and so
and so  is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.
is smoothable (see 6-manifolds: 1-connected). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem 4.1 are diffeomorphic.

5.2 Mapping class groups
...
References
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103