6-manifolds: 1-connected
m (→Examples and constructions) |
(→Introduction) |
||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | Let $\mathcal{M}_{6}$ be the set of diffeomorphism classes of [[wikipedia:Closed_manifold|closed]] [[wikipedia: | + | Let $\mathcal{M}_{6} $ |
| + | be the set of diffeomorphism classes of [[wikipedia:Closed_manifold|closed]] [[wikipedia:Differentiable_manifold|smooth]] [[wikipedia:Oriented_manifold#Orientability_of_manifolds|oriented]] | ||
| + | [[wikipedia:Simply-connected|simply-connected]] 6-manifolds $M$. | ||
| − | Similarly, let $\mathcal{M}^{\ | + | Similarly, let $\mathcal{M}^{PL}_{6}$ be the set of PL-homeomorphism classes of closed simply-connected |
| + | PL 6-manifolds and let $\mathcal{M}^{TOP}_{6}$ be the set of [[wikipedia:Homeomorphism|homeomorphism]] classes of closed simply connected [[wikipedia:Topological_manifold|topological]] $6$-manifolds. | ||
| − | In this article we report on the calculation of $\mathcal{M}^{}_{6}$ | + | In this article we report on the calculation of $\mathcal{M}^{}_{6}$, $\mathcal{M}^{PL}_{6}$ and $\mathcal{M}^{TOP}_{6}$ begun by {{cite|Smale1962}}, extended in {{cite|Wall1966}} and {{cite|Jupp1973}} and finally completed in {{cite|Zhubr2000}}. We shall write $\mathcal{M}^{\Cat}_{6}$ for either $\mathcal{M}^{}_{6}$, $\mathcal{M}^{PL}_{6}$ or $\mathcal{M}^{\Top}_{6}$. |
| + | Our first theorem is a consequence of smoothing theory for $6$-manifolds. | ||
| + | {{beginthm|Theorem}} | ||
| + | The forgetful map from smooth to PL manifolds defines a bijection | ||
| + | $\mathcal{M}_{6} \equiv \mathcal{M}^{PL}_{6}.$ | ||
| + | {{endthm}} | ||
| + | {{beginproof}} | ||
| + | To be filled in. | ||
| + | {{endproof}} | ||
An excellent summary for the case where $H_2(M)$ is torsion free may be found in {{cite|Okonek&Van de Ven1995|Section 1}}. | An excellent summary for the case where $H_2(M)$ is torsion free may be found in {{cite|Okonek&Van de Ven1995|Section 1}}. | ||
Revision as of 15:47, 12 June 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let 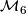 be the set of diffeomorphism classes of closed smooth oriented
simply-connected 6-manifolds
be the set of diffeomorphism classes of closed smooth oriented
simply-connected 6-manifolds  .
.
Similarly, let 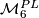 be the set of PL-homeomorphism classes of closed simply-connected
PL 6-manifolds and let
be the set of PL-homeomorphism classes of closed simply-connected
PL 6-manifolds and let 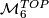 be the set of homeomorphism classes of closed simply connected topological
be the set of homeomorphism classes of closed simply connected topological  -manifolds.
-manifolds.
In this article we report on the calculation of 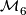 ,
, 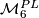 and
and 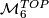 begun by [Smale1962], extended in [Wall1966] and [Jupp1973] and finally completed in [Zhubr2000]. We shall write
begun by [Smale1962], extended in [Wall1966] and [Jupp1973] and finally completed in [Zhubr2000]. We shall write 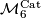 for either
for either 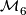 ,
, 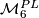 or
or 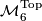 .
.
Our first theorem is a consequence of smoothing theory for  -manifolds.
-manifolds.
Theorem 1.1.
The forgetful map from smooth to PL manifolds defines a bijection
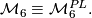
Proof. To be filled in.

An excellent summary for the case where 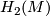 is torsion free may be found in [Okonek&Van de Ven1995, Section 1].
is torsion free may be found in [Okonek&Van de Ven1995, Section 1].
For the case where 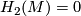 , see 6-manifolds: 2-connected.
, see 6-manifolds: 2-connected.
2 Examples and constructions
We first present some familiar 6-manifolds.
-
 , the 6-sphere.
, the 6-sphere.
-
 , the
, the  -fold connected sum of
-fold connected sum of 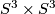 .
.
-
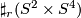 , the
, the  -fold connected sum of
-fold connected sum of 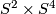 .
.
-
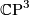 , 3-dimensional complex projective space.
, 3-dimensional complex projective space.
-
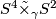 , the non-trivial linear 4-sphere bundle over
, the non-trivial linear 4-sphere bundle over  .
.
- For each
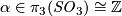 we have
we have 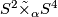 , the corresponding 2-sphere bundle over
, the corresponding 2-sphere bundle over  . If we write 1 for a generator of
. If we write 1 for a generator of 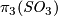 then
then 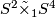 is diffeomorphic to
is diffeomorphic to 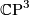 .
.
- The smooth manifold underlying any complex manifold of dimension 3 is a 1-connected 6-manifold:
- in particular, every complete intersection of complex dimension 3 is a 1-connected 6-manifold.
- Let
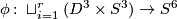 be an
be an  -component framed link and let denote by
-component framed link and let denote by 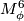 the outcome of surgery on
the outcome of surgery on  . Then
. Then 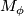 is a simply connected spinable 6-manifold with
is a simply connected spinable 6-manifold with 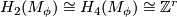 and
and 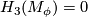 .
.
3 Invariants
The following gives a list of the key invariants needed to classify 1-connected 6-manifolds  :
:
- The 3rd Betti-number,
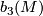 which is even since the intersection for of
which is even since the intersection for of  is skew-symmetric.
is skew-symmetric.
- The second Stiefel-Whitney class of
 is an element of
is an element of 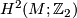 which we regard as a homomorphism
which we regard as a homomorphism 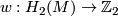 .
.
- The first Pontrjagin class
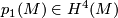 .
.
- The Kirby-Siebenmann class
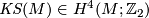 .
.
- The cup product
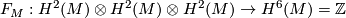 .
.
These invariants satisfy the following relation
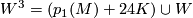
for all 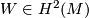 which reduce to
which reduce to 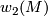 mod
mod  and for all
and for all 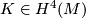 which reduce to
which reduce to 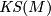 mod
mod  . As [Okonek&Van de Ven1995, p. 300] remark, in the smooth case this follows from the integrality of the
. As [Okonek&Van de Ven1995, p. 300] remark, in the smooth case this follows from the integrality of the 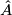 -genus but in the topological case requires further arguments carried out in [Jupp1973].
Note that if
-genus but in the topological case requires further arguments carried out in [Jupp1973].
Note that if 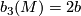 then the intersection form of
then the intersection form of  is isomorphic to
is isomorphic to  copies of
copies of 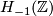 , the skew-symmetric hyperbolic form on
, the skew-symmetric hyperbolic form on 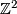 .
.
4 Classification
In this section we organise the classification results for simply-connected 6-manifolds.
4.1 Notation
Let 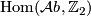 be the set of isomorphism classes of pairs
be the set of isomorphism classes of pairs 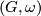 where
where  is a finitely generated abelian group
is a finitely generated abelian group 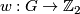 is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to
is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to  . The second Stiefel-Whitney classes defines a surjection
. The second Stiefel-Whitney classes defines a surjection
![\displaystyle w_2\co\mathcal{M}_{6}^{\Cat} \longrightarrow \Hom({\mathcal Ab}, \Zz_2), \quad \quad [M] \longmapsto w_2 : H_2(M) \to \Zz/2](/images/math/5/b/1/5b1205230c477c7fbc298e9277bf2fc0.png)
and we let ![\mathcal{M}^{\Cat}_6(G, w) = w^{-1}([G, w])](/images/math/8/0/c/80c4ca5b3295d1266199cb14719c7754.png) denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition
denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition
![\displaystyle \mathcal{M}^{\Cat}_{6} = \cup_{[G, w]} \mathcal{M}^{\Cat}_{6}(G, w)](/images/math/1/0/a/10a71e7cd3e7c1f21fa06f132840b1a0.png)
where ![[G, w]](/images/math/9/e/1/9e1553e9793f5bee0f5d92936aa7c277.png) ranges over all of
ranges over all of 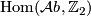 .
.
4.2 Splitting Theorem
The following theorem of Wall reduces the classification of smooth simply connected 6-manfiolds to the 2-connected case and the case where 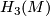 is torsion free.
is torsion free.
Theorem 3 4.1 [Wall1966, Theorem 1].
Let  be a closed, smooth, simply-connected 6-manifold with
be a closed, smooth, simply-connected 6-manifold with 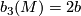 . Then up to diffeomorphism, there is a unique maniofld
. Then up to diffeomorphism, there is a unique maniofld  with
with 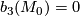 such that
such that  is diffeomorphic to
is diffeomorphic to 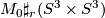 .
.
4.3 Smoothing theory
Let  be a topological 6-manifold and recall the Kirby-Siebenmann invariant
be a topological 6-manifold and recall the Kirby-Siebenmann invariant 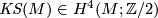 defined in [Kirby&Siebenmann1977]}: from the far reaching results of this book we have the following
defined in [Kirby&Siebenmann1977]}: from the far reaching results of this book we have the following
Theorem 4.2.
Let  be a simply-connected, topological 6-manifold. The Kirby-Siebenmann class,
be a simply-connected, topological 6-manifold. The Kirby-Siebenmann class, 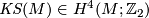 is the sole obstruction to
is the sole obstruction to  admitting a smooth structure.
admitting a smooth structure.
4.4 The case H2 is torsion free
The paper [Zhubr2000] contains a complete classification of all 1-connected 6-manifolds. However, the classification is rather complex. We state here only the classification in the case where 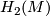 is torsion free.
is torsion free.
Recall that the following system of invariants 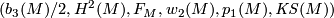 .
.
Theorem 4.3 [Jupp1973].
Let  and
and  be 1-connected 6-manifolds with
be 1-connected 6-manifolds with 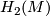 torsion free. Suppose that
torsion free. Suppose that 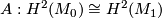 is an isomorphism of abelian groups such that
is an isomorphism of abelian groups such that
-
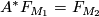 ,
,
-
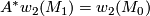 ,
,
-
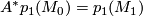 and
and
-
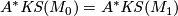 ,
,
then there is a homeomorphism 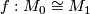 inducing
inducing  on
on 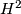 . If, in addition,
. If, in addition, 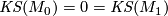 , then
, then  may be chosen to be a diffeomorphism and
may be chosen to be a diffeomorphism and 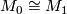 admits a unique smooth structure.
admits a unique smooth structure.
5 Further discussion
...
6 References
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Okonek&Van de Ven1995] C. Okonek and A. Van de Ven, Cubic forms and complex
 -folds, Enseign. Math. (2) 41 (1995), no.3-4, 297–333. MR1365849 (97b:32035) Zbl 0869.14018
-folds, Enseign. Math. (2) 41 (1995), no.3-4, 297–333. MR1365849 (97b:32035) Zbl 0869.14018
- [Smale1962] S. Smale, On the structure of
 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
- [Zhubr2000] A. V. Zhubr, Closed simply connected six-dimensional manifolds: proofs of classification theorems, Algebra i Analiz 12 (2000), no.4, 126–230. MR1793619 (2001j:57041)