Π-trivial map
(Difference between revisions)
(First change to explain how the two perspectives of lifts and paths relate to each other) |
(Finished the rest of relating lifts to paths) |
||
| Line 4: | Line 4: | ||
This page is based on \cite{Ranicki2002}. A map $f:N^n\to M^m$ between manifolds represents a homology class $f_*[N] \in H_n(M)$. Let $(\widetilde{M},\pi,w)$ be an [[Oriented cover|oriented cover]] with covering map $p:\widetilde{M} \to M$. If $f$ factors through $\widetilde{M}$ as $f= p\circ \widetilde{f}: N \to \widetilde{M}\to M$ then $f$ represents a homology class $\widetilde{f}_*[N]\in H_n(\widetilde{M})$. Note that a '''choice''' of lift $\widetilde{f}$ is required in order to represent a homology class. | This page is based on \cite{Ranicki2002}. A map $f:N^n\to M^m$ between manifolds represents a homology class $f_*[N] \in H_n(M)$. Let $(\widetilde{M},\pi,w)$ be an [[Oriented cover|oriented cover]] with covering map $p:\widetilde{M} \to M$. If $f$ factors through $\widetilde{M}$ as $f= p\circ \widetilde{f}: N \to \widetilde{M}\to M$ then $f$ represents a homology class $\widetilde{f}_*[N]\in H_n(\widetilde{M})$. Note that a '''choice''' of lift $\widetilde{f}$ is required in order to represent a homology class. | ||
| − | By covering space theory (c.f. \cite{Hatcher2002|Proposition 1.33}) a map $f:N\to M$ can be lifted to $\widetilde{M}$ if and only if $f_*(\pi_1(N)) \subset p_*(\pi_1(\widetilde{M}))$, i.e. if and only if the composition $q\circ f_*:\pi_1(N)\to \pi_1(M) \to \pi$ is trivial for $q:\pi_1(M)\to \pi_1(M)/\pi_1(\widetilde{M} | + | Let $b_1$ be a basepoint of $N$. By covering space theory (c.f. \cite{Hatcher2002|Proposition 1.33}) a map $f:N\to M$ can be lifted to $\widetilde{M}$ if and only if $f_*(\pi_1(N,b_1)) \subset p_*(\pi_1(\widetilde{M},\widetilde{f(b_1)}))$, i.e. if and only if the composition $q\circ f_*:\pi_1(N,b_1)\to \pi_1(M,f(b_1)) \to \pi$ is trivial for $q:\pi_1(M,f(b_1))\to \pi:=\pi_1(M,f(b_1))/\pi_1(\widetilde{M},\widetilde{f(b_1)})$ the quotient map. |
| + | |||
| + | The group $\pi$ is well-defined for any choice of lift $\widetilde{f(b_1)}$ since $p:\widetilde{M}\to M$ is a regular covering and changing the basepoint in $\widetilde{M}$ to a different lift corresponds to conjugating $\pi_1(\widetilde{M},\widetilde{f(b_1)})$ by some $g\in \pi_1(M,f(b_1))$. | ||
</wikitex> | </wikitex> | ||
== Definition == | == Definition == | ||
<wikitex>; | <wikitex>; | ||
| − | Let $M$ be an $m$-dimensional manifold and let $(\widetilde{M},\pi,w)$ be an [[Oriented cover|oriented cover]]. A '''$\pi$-trivial map''' $f:N^n\to M^m$ is a map from an oriented manifold $N$ | + | Let $M$ be an $m$-dimensional manifold and let $(\widetilde{M},\pi,w)$ be an [[Oriented cover|oriented cover]]. A '''$\pi$-trivial map''' $f:N^n\to M^m$ is a map from an oriented manifold $N$ with basepoint $b_1$ such that the composite |
$$\xymatrix{ | $$\xymatrix{ | ||
| − | \pi_1(N) \ar[r]^-{f_*} & \pi_1(M) \ar[r] & \pi | + | \pi_1(N,b_1) \ar[r]^-{f_*} & \pi_1(M,f(b_1)) \ar[r] & \pi |
}$$ | }$$ | ||
| − | is trivial. | + | is trivial, together with a choice of lift $\widetilde{f}:N \to \widetilde{M}$. |
</wikitex> | </wikitex> | ||
== Properties == | == Properties == | ||
| Line 22: | Line 24: | ||
== Lifts and paths - two alternative perspectives == | == Lifts and paths - two alternative perspectives == | ||
<wikitex>; | <wikitex>; | ||
| − | Since $\pi$ is the group of deck transformations of $\widetilde{M}$, the set of lifts $\{\widetilde{f}:N\to \widetilde{M}\}$ is non-canonically isomorphic to $\pi$ with the group structure determined by the action of $\pi$ once | + | Rather than taking a lift as part of the data for a $\pi$-trivial map we could instead take an equivalence class of paths in $M$ as is explained in this section. Since $\pi$ is the group of deck transformations of $\widetilde{M}$, the set of lifts $\{\widetilde{f}:N\to \widetilde{M}\}$ is non-canonically isomorphic to $\pi$ with the group structure determined by the action of $\pi$ once a choice of lift $\widetilde{f}_{id}$ has been chosen to represent the identity element. In this way the choice of lift that is included as part of the data of a $\pi$-trivial map can be thought of as a choice of isomorphism $$ \begin{array}{rcl} \{\widetilde{f}:N\to \widetilde{M}\} & \stackrel{\simeq}{\longrightarrow} & \pi \\ \widetilde{f} & \mapsto & g\;s.t.\; \widetilde{f}(b_1) = g\widetilde{f}_{id}(b_1).\end{array}$$ |
| + | Let $b$ be a basepoint of $M$. The set of homotopy classes of paths from $b$ to $f(b_1)$ is non-canonically isomophic to $\pi_1(M,b)$. An isomorphism is defined by a choice of path $[w_{id}]$ to represent the identity element: $$\begin{array}{rcl} \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}& \to & \pi_1(M,b)\\ [w] &\mapsto & [w_{id}^{-1}*w],\end{array}$$where $*$ denotes concatenation of paths and $w_{id}^{-1}$ is the path $w_{id}$ in reverse. Let $\widetilde{b}$ be a basepoint of $\widetilde{M}$ that is a lift of $b$. | ||
| + | |||
| + | Define an equivalence relation $\sim$ on this set by saying $$[w]\sim[w^\prime] \iff [w^{-1}*w^\prime] \in p_*(\pi_1(\widetilde{M},\widetilde{b})).$$ The above isomorphism given by choosing $[w_{id}]$ descends to give an isomorphism $$\{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim \;\longrightarrow\; \pi_1(M,b)/\pi_1(\widetilde{M},\widetilde{b})\cong \pi,$$ where we use the same choice of path $[w_{id}]$ to identify $\pi_1(M,b)/\pi_1(\widetilde{M},\widetilde{b}) $ with $\pi_1(M,f(b_1))/\pi_1(\widetilde{M},\widetilde{f(b_1)})=\pi$. | ||
| + | |||
| + | Thus a choice of lift $\widetilde{f}:N\to \widetilde{M}$ corresponds to a choice of homotopy class of paths from $b$ to $f(b_1)$ modulo $\pi_1(\widetilde{M})$. A choice of lift $\widetilde{b}$ defines a bijection of sets $$\{\widetilde{f}:N\to \widetilde{M}\} \longleftrightarrow \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim$$ as follows. Given a choice of lift $\widetilde{f}$ choose any path $\widetilde{w}:I \to \widetilde{M}$ from $\widetilde{b}$ to $\widetilde{f}(b_1)$. Take the equivalence class of $p(\widetilde{w})$ which is a path in $M$ from $b$ to $f(b_1)$. Conversely given a choice of class $$[w]\in \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim$$ choose any representative $w:I \to M$. This lifts uniquely to a path $\widetilde{w}$ starting at $\widetilde{b}$. Define a lift $\widetilde{f}$ by setting $\widetilde{f}(b_1):= \widetilde{w}(1)$. Note this map is well-defined since different choices of representative $w$ may differ by elements of $\pi_1(\widetilde{M},\widetilde{b})$ but their lifts will still end at the same point. | ||
| + | To sum up we have the following diagram of non-canonical isomorphisms and bijections | ||
| + | $$\xymatrix{ \{\widetilde{f}:N\to \widetilde{M}\} \ar@{<->}[rr]^-{\widetilde{b}} \ar[dr]_-{\widetilde{f}_{id}} && \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim \ar[dl]^-{[w_{id}]} \\ & \pi & }.$$ Each map is obtained by making a choice and any two choices uniquely determine the third with the diagram commuting, so with two choices made the horizontal bijection is in fact an isomorphism of groups. | ||
</wikitex> | </wikitex> | ||
Revision as of 15:59, 2 May 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
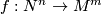 between manifolds represents a homology class
between manifolds represents a homology class ![f_*[N] \in H_n(M)](/images/math/3/d/2/3d21d4bf00b5770f8382bf0d70aa035e.png) . Let
. Let 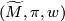 be an oriented cover with covering map
be an oriented cover with covering map 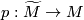 . If
. If  factors through
factors through Tex syntax erroras
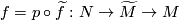 then
then  represents a homology class
represents a homology class ![\widetilde{f}_*[N]\in H_n(\widetilde{M})](/images/math/c/a/a/caa1901615f9a1811d1f344376d0e5a2.png) . Note that a choice of lift
. Note that a choice of lift 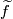 is required in order to represent a homology class.
Let
is required in order to represent a homology class.
Let 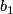 be a basepoint of
be a basepoint of  . By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map
. By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map 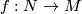 can be lifted to
can be lifted to Tex syntax errorif and only if
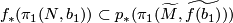 , i.e. if and only if the composition
, i.e. if and only if the composition 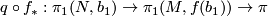 is trivial for
is trivial for 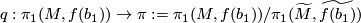 the quotient map.
The group
the quotient map.
The group  is well-defined for any choice of lift
is well-defined for any choice of lift 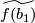 since
since 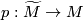 is a regular covering and changing the basepoint in
is a regular covering and changing the basepoint in Tex syntax errorto a different lift corresponds to conjugating
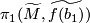 by some
by some 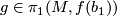 .
.
2 Definition
Let  be an
be an  -dimensional manifold and let
-dimensional manifold and let 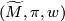 be an oriented cover. A
be an oriented cover. A  -trivial map
-trivial map 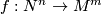 is a map from an oriented manifold
is a map from an oriented manifold  with basepoint
with basepoint 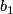 such that the composite
such that the composite
![\displaystyle \xymatrix{ \pi_1(N,b_1) \ar[r]^-{f_*} & \pi_1(M,f(b_1)) \ar[r] & \pi }](/images/math/c/e/3/ce3bcb9515d2da35fe37b876a521d6bb.png)
is trivial, together with a choice of lift 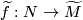 .
.
3 Properties
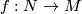 that factors through
that factors through Tex syntax errormust map all of
 to the same sheet of
to the same sheet of Tex syntax error, hence the pullback satisfies
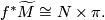
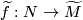 , which thought of as a map from
, which thought of as a map from 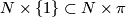 extends equivariantly to a lift
extends equivariantly to a lift 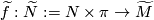 .
.
4 Lifts and paths - two alternative perspectives
 -trivial map we could instead take an equivalence class of paths in
-trivial map we could instead take an equivalence class of paths in  as is explained in this section. Since
as is explained in this section. Since  is the group of deck transformations of
is the group of deck transformations of Tex syntax error, the set of lifts
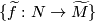 is non-canonically isomorphic to
is non-canonically isomorphic to  with the group structure determined by the action of
with the group structure determined by the action of  once a choice of lift
once a choice of lift 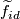 has been chosen to represent the identity element. In this way the choice of lift that is included as part of the data of a
has been chosen to represent the identity element. In this way the choice of lift that is included as part of the data of a  -trivial map can be thought of as a choice of isomorphism
-trivial map can be thought of as a choice of isomorphism 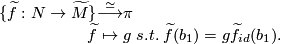
 be a basepoint of
be a basepoint of  . The set of homotopy classes of paths from
. The set of homotopy classes of paths from  to
to 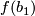 is non-canonically isomophic to
is non-canonically isomophic to 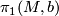 . An isomorphism is defined by a choice of path
. An isomorphism is defined by a choice of path ![[w_{id}]](/images/math/4/7/b/47b28a80ac5a68297110c29b79855b6c.png) to represent the identity element:
to represent the identity element: Tex syntax error
 denotes concatenation of paths and
denotes concatenation of paths and 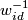 is the path
is the path 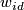 in reverse. Let
in reverse. Let 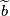 be a basepoint of
be a basepoint of Tex syntax errorthat is a lift of
 .
Define an equivalence relation
.
Define an equivalence relation 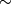 on this set by saying
on this set by saying ![\displaystyle [w]\sim[w^\prime] \iff [w^{-1}*w^\prime] \in p_*(\pi_1(\widetilde{M},\widetilde{b})).](/images/math/9/8/0/98019a1469641c8c2762306f91700b0c.png)
![[w_{id}]](/images/math/4/7/b/47b28a80ac5a68297110c29b79855b6c.png) descends to give an isomorphism
descends to give an isomorphism ![\displaystyle \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim \;\longrightarrow\; \pi_1(M,b)/\pi_1(\widetilde{M},\widetilde{b})\cong \pi,](/images/math/2/6/0/26029500a0f65bc7905fbbbffaa82d91.png)
![[w_{id}]](/images/math/4/7/b/47b28a80ac5a68297110c29b79855b6c.png) to identify
to identify 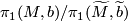 with
with 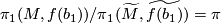 .
Thus a choice of lift
.
Thus a choice of lift 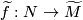 corresponds to a choice of homotopy class of paths from
corresponds to a choice of homotopy class of paths from  to
to 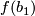 modulo
modulo 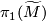 . A choice of lift
. A choice of lift 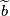 defines a bijection of sets
defines a bijection of sets ![\displaystyle \{\widetilde{f}:N\to \widetilde{M}\} \longleftrightarrow \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim](/images/math/3/b/9/3b91a8a4595ed359f53fa3eb5a0753e0.png)
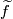 choose any path
choose any path 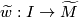 from
from 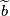 to
to 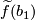 . Take the equivalence class of
. Take the equivalence class of 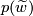 which is a path in
which is a path in  from
from  to
to 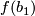 . Conversely given a choice of class
. Conversely given a choice of class ![\displaystyle [w]\in \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim](/images/math/c/9/e/c9ee0bc2859bb8ef4b1bb6508c79e344.png)
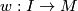 . This lifts uniquely to a path
. This lifts uniquely to a path 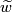 starting at
starting at 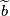 . Define a lift
. Define a lift 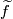 by setting
by setting 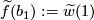 . Note this map is well-defined since different choices of representative
. Note this map is well-defined since different choices of representative  may differ by elements of
may differ by elements of 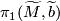 but their lifts will still end at the same point.
but their lifts will still end at the same point.
To sum up we have the following diagram of non-canonical isomorphisms and bijections
![\displaystyle \xymatrix{ \{\widetilde{f}:N\to \widetilde{M}\} \ar@{<->}[rr]^-{\widetilde{b}} \ar[dr]_-{\widetilde{f}_{id}} && \{[w:I\to M]: w(0)=b,\,w(1)=f(b_1)\}/\sim \ar[dl]^-{[w_{id}]} \\ & \pi & }.](/images/math/d/3/d/d3d9b5d962bbd6495f83ad8b4d389724.png)
5 Examples
...
6 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001