Π-trivial map
(Difference between revisions)
m |
(First change to explain how the two perspectives of lifts and paths relate to each other) |
||
| Line 18: | Line 18: | ||
<wikitex>; | <wikitex>; | ||
A map $f:N\to M$ that factors through $\widetilde{M}$ must map all of $N$ to the same sheet of $\widetilde{M}$, hence the pullback satisfies $$f^*\widetilde{M} \cong N\times \pi.$$ Choosing where to lift a single point determines a lift $\widetilde{f}:N \to \widetilde{M}$, which thought of as a map from $N\times \{1\} \subset N \times \pi$ extends equivariantly to a lift $\widetilde{f}:\widetilde{N}:=N\times \pi \to \widetilde{M}$. | A map $f:N\to M$ that factors through $\widetilde{M}$ must map all of $N$ to the same sheet of $\widetilde{M}$, hence the pullback satisfies $$f^*\widetilde{M} \cong N\times \pi.$$ Choosing where to lift a single point determines a lift $\widetilde{f}:N \to \widetilde{M}$, which thought of as a map from $N\times \{1\} \subset N \times \pi$ extends equivariantly to a lift $\widetilde{f}:\widetilde{N}:=N\times \pi \to \widetilde{M}$. | ||
| + | </wikitex> | ||
| + | |||
| + | == Lifts and paths - two alternative perspectives == | ||
| + | <wikitex>; | ||
| + | Since $\pi$ is the group of deck transformations of $\widetilde{M}$, the set of lifts $\{\widetilde{f}:N\to \widetilde{M}\}$ is non-canonically isomorphic to $\pi$ with the group structure determined by the action of $\pi$ once an identity element lift $\widetilde{f}_{id}$ has been chosen. In this way the choice of lift that is included as part of the data of a $\pi$-trivial map can be thought of as a choice of isomorphism $$ \begin{array}{rcl} \{\widetilde{f}:N\to \widetilde{M}\} & \stackrel{\simeq}{\longrightarrow} & \pi \\ \widetilde{f} & \mapsto & g\;s.t.\; \widetilde{f} = g\widetilde{f}_{id}.\end{array}$$ | ||
</wikitex> | </wikitex> | ||
Revision as of 10:54, 2 May 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
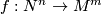 between manifolds represents a homology class
between manifolds represents a homology class ![f_*[N] \in H_n(M)](/images/math/3/d/2/3d21d4bf00b5770f8382bf0d70aa035e.png) . Let
. Let 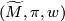 be an oriented cover with covering map
be an oriented cover with covering map 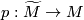 . If
. If  factors through
factors through Tex syntax erroras
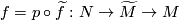 then
then  represents a homology class
represents a homology class ![\widetilde{f}_*[N]\in H_n(\widetilde{M})](/images/math/c/a/a/caa1901615f9a1811d1f344376d0e5a2.png) . Note that a choice of lift
. Note that a choice of lift 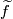 is required in order to represent a homology class.
By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map
is required in order to represent a homology class.
By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map 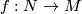 can be lifted to
can be lifted to Tex syntax errorif and only if
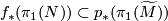 , i.e. if and only if the composition
, i.e. if and only if the composition 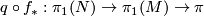 is trivial for
is trivial for 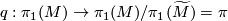 the quotient map.
the quotient map.
2 Definition
Let  be an
be an  -dimensional manifold and let
-dimensional manifold and let 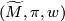 be an oriented cover. A
be an oriented cover. A  -trivial map
-trivial map 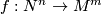 is a map from an oriented manifold
is a map from an oriented manifold  , together with a choice of lift
, together with a choice of lift 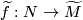 , such that the composite
, such that the composite
![\displaystyle \xymatrix{ \pi_1(N) \ar[r]^-{f_*} & \pi_1(M) \ar[r] & \pi }](/images/math/a/f/6/af62534d631fe62ab4fd71ba1af6a259.png)
is trivial.
3 Properties
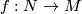 that factors through
that factors through Tex syntax errormust map all of
 to the same sheet of
to the same sheet of Tex syntax error, hence the pullback satisfies
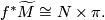
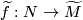 , which thought of as a map from
, which thought of as a map from 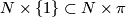 extends equivariantly to a lift
extends equivariantly to a lift 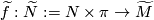 .
.
4 Lifts and paths - two alternative perspectives
 is the group of deck transformations of
is the group of deck transformations of Tex syntax error, the set of lifts
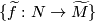 is non-canonically isomorphic to
is non-canonically isomorphic to  with the group structure determined by the action of
with the group structure determined by the action of  once an identity element lift
once an identity element lift 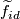 has been chosen. In this way the choice of lift that is included as part of the data of a
has been chosen. In this way the choice of lift that is included as part of the data of a  -trivial map can be thought of as a choice of isomorphism
-trivial map can be thought of as a choice of isomorphism 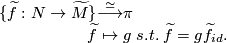
5 Examples
...
6 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001