Knots, i.e. embeddings of spheres
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
We work in a smooth category. In particular, terms embedding and smooth embedding or map and smooth map are used interchangeably. For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
2 Examples
There are smooth embeddings 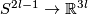 which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
Example 2.1. (a) Analogously to the Haefliger trefoil knot for any  one constructs a smooth embedding
one constructs a smooth embedding 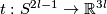 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For 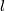 even
even 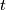 is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding; 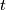 represents a generator of
represents a generator of 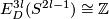 [Haefliger1962].
[Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 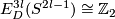 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 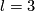 .
.
(b) For any 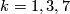 let
let 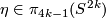 be the homotopy class of the Hopf map.
Denote by
be the homotopy class of the Hopf map.
Denote by 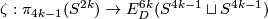 the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum
the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum 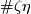 of the components of (a representative of)
of the components of (a representative of) 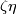 is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding; 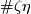 is a generator of
is a generator of 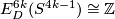 [Skopenkov2015a, Corollary 2.13].
[Skopenkov2015a, Corollary 2.13].
3 Invariants
Let us define the Haefliger invariant 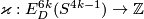 .
The definition is motivated by Haefliger's proof that any embedding
.
The definition is motivated by Haefliger's proof that any embedding 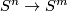 is isotopic to the standard embedding for
is isotopic to the standard embedding for 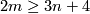 , and by analyzing what obstructs carrying this proof for
, and by analyzing what obstructs carrying this proof for 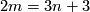 .
.
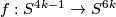 has a framing extendable to a framed embedding
has a framing extendable to a framed embedding 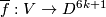 of a
of a  -manifold
-manifold  whose boundary is
whose boundary is 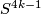 , and whose signature is zero. For an integer
, and whose signature is zero. For an integer 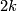 -cycle
-cycle  in
in  let
let 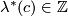 be the linking number of
be the linking number of 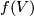 with a slight shift of
with a slight shift of 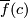 along the first vector of the framing. This defines a map
along the first vector of the framing. This defines a map 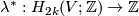 . This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique
. This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique 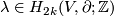 such that
such that ![\lambda^*[c]=\lambda\cap_V[c]](/images/math/b/2/8/b2878e69f979f9a0ca580faf4d104941.png) for any
for any ![[c]\in H_{2k}(V;\Z)](/images/math/8/9/f/89f1bbfc9e8e5259c8e842991bb8018b.png) . Since
. Since  has a normal framing, its intersection form
has a normal framing, its intersection form 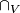 is even. (Indeed, represent a class in
is even. (Indeed, represent a class in 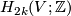 by a closed oriented
by a closed oriented 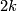 -submanifold
-submanifold  . Then
. Then ![\rho_2[c]\cap_V[c]=\overline{w_{2k}}(c\subset V)=\rho_2[c]\cap_VPDw_{2k}(V)=0](/images/math/7/8/8/788a4e3686035885f1e93cfe29a761c1.png) because
because  has a normal framing.) Hence
has a normal framing.) Hence 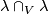 is an even integer. Define
is an even integer. Define 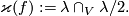
Since the signature of  is zero, there is a symplectic basis
is zero, there is a symplectic basis 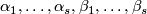 in
in 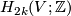 .
Then clearly
.
Then clearly
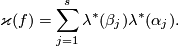
For an alternative definition via Seifert surfaces in 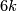 -space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,
-space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,  4].
4].
Sketch of a proof that 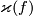 is well-defined (i.e. is independent of
is well-defined (i.e. is independent of  ,
, 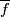 , and the framings), and is invariant under isotopy of
, and the framings), and is invariant under isotopy of  . [Haefliger1962, Theorem 2.6]
Analogously one defines
. [Haefliger1962, Theorem 2.6]
Analogously one defines 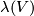 and
and 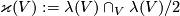 for a framed
for a framed  -submanifold
-submanifold  of
of 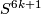 . Since
. Since 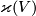 is a characteristic number, it is independent of framed cobordism. So
is a characteristic number, it is independent of framed cobordism. So 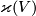 defines a homomorphism
defines a homomorphism 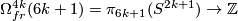 . The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
. The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
Since 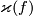 is a characteristic number, it is independent of framed cobordism of a framed
is a characteristic number, it is independent of framed cobordism of a framed  (and hence of the isotopy of a framed
(and hence of the isotopy of a framed  ).
).
Therefore 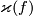 is a well-defined invariant of a framed cobordism class of a framed
is a well-defined invariant of a framed cobordism class of a framed  . By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3])
. By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3]) 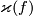 is also independent of the framing of
is also independent of the framing of  extendable to a framing of some
extendable to a framing of some  -manifold
-manifold  having trivial signature. QED
having trivial signature. QED
For definition of the attaching invariant 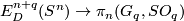 see [Haefliger1966], [Skopenkov2005,
see [Haefliger1966], [Skopenkov2005,  3].
3].
4 Classification
Theorem 4.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 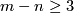 the group
the group 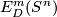 is finite unless
is finite unless 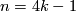 and
and 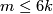 , when
, when 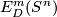 is the sum of
is the sum of  and a finite group.
and a finite group.
Theorem 4.2 (Haefliger-Milgram).
We have the following table for the group 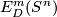 ; in the whole table
; in the whole table 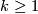 ; in the fifth column
; in the fifth column 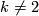 ; in the last two columns
; in the last two columns 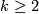 :
:
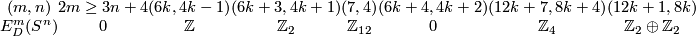
Proof for the first four columns, and for the fifth column when  is odd, are presented in [Haefliger1966, 8.15] (see also
is odd, are presented in [Haefliger1966, 8.15] (see also  6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,
6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]; there is a typo in [Haefliger1966, 8.15]:
3]; there is a typo in [Haefliger1966, 8.15]: 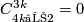 should be
should be 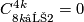 ). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases
). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases 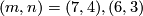 are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
Theorem 4.3 [Milgram1972, Corollary G].
We have 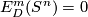 if and only if either
if and only if either 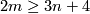 , or
, or 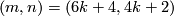 ,
or
,
or 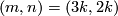 and
and 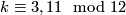 ,
or
,
or 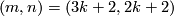 and
and 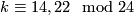 .
.
For a description of 2-components of 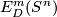 see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
The lowest-dimensional unknown groups 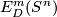 are
are 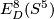 and
and 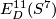 .
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
.
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
For  the group
the group 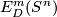 has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 4.4 [Haefliger1966].
For 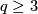 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
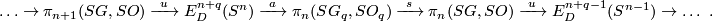
Here 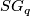 is the space of maps
is the space of maps 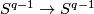 of degree
of degree  . Restricting a map from
. Restricting a map from 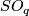 to
to 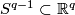 identifies
identifies 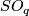 as a subspace of
as a subspace of 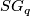 . Define
. Define 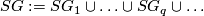 . Analogously define
. Analogously define 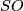 . Let
. Let  be the stabilization homomorphism. The attaching invariant
be the stabilization homomorphism. The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
5 Some remarks on codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 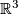 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
6 Proof of classification of (4k-1)-knots in 6k-space
Theorem 6.1.
The Haefliger invariant 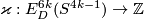 is injective for
is injective for 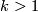 .
.
The proof is a certain simplification of [Haefliger1962]. We present an exposition structured to make it more accessible to non-specialists.
Lemma 6.2.
Let  be a framed
be a framed 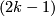 -connected
-connected  -submanifold of
-submanifold of 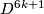 such that
such that 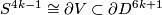 , signature of
, signature of  is zero, and
is zero, and 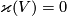 .
Then there is an embedding
.
Then there is an embedding 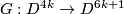 such that
such that 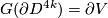 .
.
Proof of Theorem 6.1 using Lemma 6.2.
By the first three paragraphs of the proof of Theorem 3.1 in ???[Ha62], for any embedding 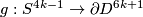 such that
such that 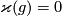 there is a framed
there is a framed 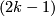 -connected
-connected  -submanifold
-submanifold  of
of 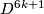 with zero signature such that
with zero signature such that 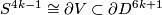 and
and 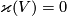 . Then from Lemma 6.2 it follows that there is an extension
. Then from Lemma 6.2 it follows that there is an extension 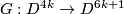 such that
such that 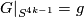 .
From Smale Theorem it follows that
.
From Smale Theorem it follows that  is isotopic to the standard embedding.
is isotopic to the standard embedding.

To prove Lemma 6.2 we need Lemma 6.3, Lemma 6.4 and Lemma 6.5.
All the manifolds below can have non-empty boundaries.
Lemma 6.3 [Whitney lemma].
Let 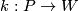 be a map from a connected
be a map from a connected  -manifold
-manifold  to a simply connected
to a simply connected 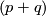 -manifold
-manifold  . If
. If 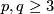 , then
, then
- There is a homotopy
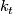 such that
such that 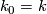 and
and 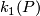 is an embedding.???
is an embedding.???
- Suppose in addition that there is a map
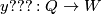 from a connected
from a connected  -manifold
-manifold 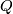 such that the algebraic intersection number??? of
such that the algebraic intersection number??? of 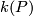 and
and 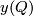 is zero. Then there is a homotopy
is zero. Then there is a homotopy 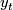 relative to the boundary such that
relative to the boundary such that 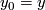 and
and 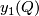 does not intersect
does not intersect 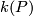 . If
. If  is an embedding, the homotopy
is an embedding, the homotopy 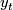 can be chosen so that
can be chosen so that 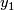 is an embedding.
is an embedding.
Lemma 6.4. Let  be a
be a 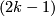 -connected
-connected  -manifold, and
-manifold, and 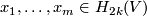 are such that
are such that 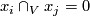 for every
for every 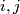 .
Then there are embeddings
.
Then there are embeddings 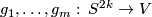 with pairwise disjoint images representing
with pairwise disjoint images representing 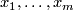 , respectively.
, respectively.
Proof. As  is
is 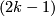 -connected, the Hurewicz map
-connected, the Hurewicz map 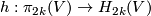 is an isomorphism. For an element
is an isomorphism. For an element 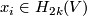 , let
, let 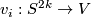 represent the homotopy class
represent the homotopy class 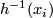 .
Now we perform the following inductive procedure.
At the
.
Now we perform the following inductive procedure.
At the  -th step of the procedure assume that the maps
-th step of the procedure assume that the maps 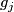 from the assertion are already constructed for any
from the assertion are already constructed for any 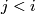 , and we construct
, and we construct 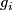 .
First, applying item 1 of Lemma 6.3 to
.
First, applying item 1 of Lemma 6.3 to 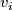 ,
we may suppose that
,
we may suppose that 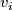 itself is an embedding.
Further, we apply item 2 of Lemma 6.3, ???setting
itself is an embedding.
Further, we apply item 2 of Lemma 6.3, ???setting 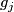 as
as  ,
, 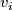 as
as  , and
, and 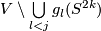 as
as  , for any
, for any 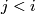 .
???Observe that Lemma 6.3 is applicable as
.
???Observe that Lemma 6.3 is applicable as 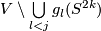 is simply connected provided
is simply connected provided 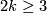 and
and  is simply connected.
Also, as
is simply connected.
Also, as 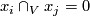 for any
for any  ,
,  , the algebraic intersection number for all the pairs of maps above??? is zero.
As the result,
, the algebraic intersection number for all the pairs of maps above??? is zero.
As the result, 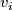 is replaced with a homotopic embedding
is replaced with a homotopic embedding 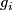 , and the images of
, and the images of 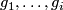 are disjoint.
After the step
are disjoint.
After the step  we obtain the ???desired set of embeddings.
we obtain the ???desired set of embeddings.

Lemma 6.5.[cf. Proposition 3.3 in [Ha62]]
Let  be an orientable
be an orientable  -submanifold of
-submanifold of 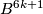 , and
, and 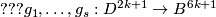 be embeddings with pairwise disjoint images such that
be embeddings with pairwise disjoint images such that 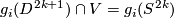 ,
, 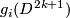 are orthogonal to
are orthogonal to  , and over every
, and over every 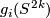 the manifold
the manifold  has a framing whose first vector is tangent to
has a framing whose first vector is tangent to 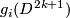 .
Assume that
.
Assume that 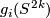 has zero algebraic self-intersection in
has zero algebraic self-intersection in  for every
for every  .
Then there are embeddings
.
Then there are embeddings 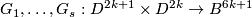 extending
extending 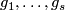 such that
such that 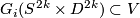 for every
for every  .
.
Proof. By general position, it suffices to prove the existence of 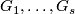 for
for 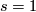 .
So assume that
.
So assume that 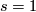 .
Since
.
Since 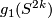 has zero algebraic self-intersection in
has zero algebraic self-intersection in  , the Euler class of the normal bundle of
, the Euler class of the normal bundle of 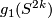 in
in  is zero.
Hence
is zero.
Hence 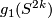 has a framing in
has a framing in  .
.
Identify all the normal spaces!!! of 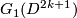 with the normal space at
with the normal space at 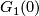 .
The normal framing
.
The normal framing  of
of 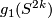 in
in  is orthogonal to
is orthogonal to 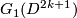 .
So
.
So  defines a map
defines a map 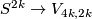 .
Let
.
Let 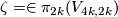 be the homotopy class of this map.
This is the obstruction to extending
be the homotopy class of this map.
This is the obstruction to extending  to a normal
to a normal 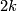 -framing of
-framing of 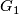 in
in 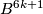 (so apriori
(so apriori 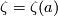 ).
It suffices to prove that
).
It suffices to prove that 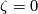 .
.
Consider the exact sequence of the bundle 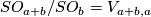 :
:
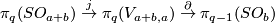 .
By the following well-known assertion,
.
By the following well-known assertion, 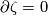 :
if
:
if 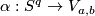 is a map, then
is a map, then ![\partial[\alpha]](/images/math/2/e/d/2edf6536f43980cf8085e5b147dbf8dd.png) is the obstruction to trivialization of the orthogonal complement to the field of
is the obstruction to trivialization of the orthogonal complement to the field of  -frames in
-frames in 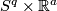 corresponding to
corresponding to  .
By [Fomenko&Fuchs2016, Corollary in
.
By [Fomenko&Fuchs2016, Corollary in  25.4]
25.4] 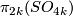 is a finite group.
Since
is a finite group.
Since 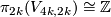 , we obtain that
, we obtain that 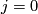 for
for 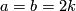 .
This and
.
This and 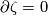 imply that
imply that 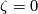 .
.
(In [Haefliger1962, the last but one paragraph of 3.5] perhaps one has to replace `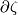 is the obstruction to trivializing the normal bundle of
is the obstruction to trivializing the normal bundle of 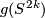 in
in  ' by `
' by `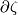 is the obstruction to trivializing te orthogonal complement to the
is the obstruction to trivializing te orthogonal complement to the  -direction of the normal bundle of
-direction of the normal bundle of  restricted to
restricted to 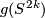 '?)
'?)
(No, as we use different obstruction; our is orthogonal to Haefliger's)
Alternatively:
Consider a map of the long exact sequences associated to the inclusion 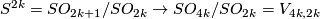 :
:
![\xymatrix{\pi_{2k}(SO_{2k+1}) \ar[r]^{p = 0} \ar[d]^{s} & \pi_{2k}(S^{2k}) \ar[d] \\ \pi_{2k}(SO_{4k})\ar[r]^{p'=0} & \pi_{2k}(V_{4k, 2k})\ar[r]^{\partial '} & \pi_{2k-1}(SO_{2k})}](/images/math/6/b/d/6bd84decbb0eed604d0acdc67e0ef956.png)
By [Fomenko&Fuchs2016, Corollary in  25.4]
25.4] 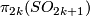 is a finite group.
Since
is a finite group.
Since 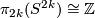 , we obtain that
, we obtain that 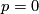 .
Since
.
Since  is surjective, we obtain that
is surjective, we obtain that 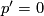 .
.
Hence 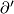 is injective.
The class
is injective.
The class 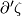 is??? the obstruction to trivializing the orthogonal complement of
is??? the obstruction to trivializing the orthogonal complement of 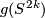 ,
cf. [Haefliger1962, 3.4, Lemma].
,
cf. [Haefliger1962, 3.4, Lemma].
Suggestion: interpreting 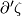 as an obstruction, we derive that
as an obstruction, we derive that 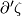 is zero, as
is zero, as  is framed and the first vector of the framing is tangent to
is framed and the first vector of the framing is tangent to 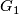 .
.
Therefore, 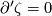 .
Since
.
Since 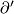 is injective, we obtain
is injective, we obtain 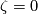 .
.

Lemma 6.6.
Denote by 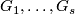 the embeddings from Lemma 6.5.
There is smooth manifold
the embeddings from Lemma 6.5.
There is smooth manifold 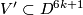 such that
such that 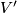 is homeomorphic to the
is homeomorphic to the 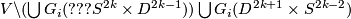 and
and 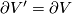 .
.
Proof.
For any 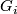 choose smole??? neighborhood
choose smole??? neighborhood 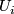 of
of 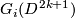 and smooth diffeomorphism
and smooth diffeomorphism 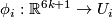 such that
such that 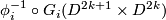 is defined by
is defined by 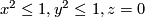 in some coordinates
in some coordinates 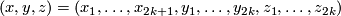 of
of 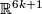 .
.
Denote by 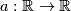 a smooth monotonous map such that
a smooth monotonous map such that 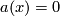 for
for 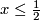 and
and 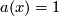 for
for 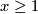 .
Denote by
.
Denote by 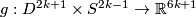 the smooth map, defined by the formula
the smooth map, defined by the formula 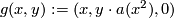 .
Take by
.
Take by 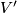 the manifold
the manifold 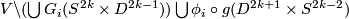 .
.
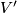 is homeomorphic to
is homeomorphic to  .
Therefore, map
.
Therefore, map 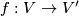 defined by equation
defined by equation 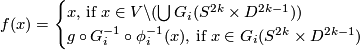 is the homeomorphism.
Since
is the homeomorphism.
Since 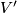 coincide with
coincide with  outside the
outside the 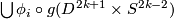 and
and 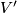 is smooth in
is smooth in 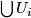 , we have that
, we have that 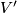 is smooth.
is smooth.

Below the symbol ![[ \cdot ]](/images/math/6/3/8/6381c926ef9f50dd3b996dc8f184f777.png) denotes the integral fundamental class of a manifold or the homotopy class of a map, depending on the context.
denotes the integral fundamental class of a manifold or the homotopy class of a map, depending on the context.
Proof of Lemma 6.2 using Lemmas 6.4, 6.5..
By the fourth paragraph of the proof of Theorem 3.1 in [Ha62], there is a basis 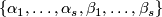 in
in 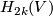 such that
such that 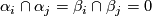 ,
, 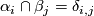 and
and 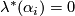 for any
for any 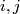 .
From Lemma 6.4 it follows that there are embeddings
.
From Lemma 6.4 it follows that there are embeddings 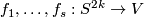 with pairwise disjoint images such that
with pairwise disjoint images such that ![f_{1*}[S^{2k}]=\alpha_1, \ldots, f_{s*}[S^{2k}]=\alpha_s](/images/math/1/e/6/1e653b0c9d960d04483687b85c44b6ae.png) .
.
Denote by 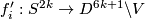 for
for 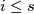 the result of shifting of
the result of shifting of  by the first vector of the framing of
by the first vector of the framing of  .
Since
.
Since ![\lambda(f_{i*}[S^{2k}])=\lambda(\alpha_i)=0](/images/math/7/9/e/79ebf45af7d2df318b2b16ac4643723a.png) , we have
, we have ![f_{i*}'([S^{2k}])=0 \in H_{2k}(D^{6k+1}\backslash V)](/images/math/0/c/7/0c71be9dfcfc35fd855384af104ad878.png) .
Since
.
Since 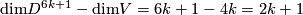 , we have
, we have 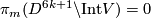 for
for 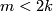 .
Since
.
Since ![f_{i*}'([S^{2k}])=0\in H_{2k}(D^{6k+1}\backslash V)](/images/math/3/4/2/342380eb09f0370d54cdfd9b6149a305.png) , we have
, we have ![[f_i']=0\in \pi_{2k}(D^{6k+1}\backslash V)](/images/math/7/0/9/70960bf349acf335d2500d28dad3c923.png) .
Therefore there are extensions of
.
Therefore there are extensions of 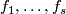 to maps
to maps 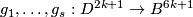 such that
such that 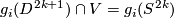 .
.
???Set  such that
such that 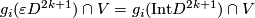 .
As
.
As ![\lambda^*(g_{i*}[S^{2k}])=0](/images/math/b/0/e/b0ed2eb29e6150331d761149d5c8834d.png) for any
for any  , the algebraic intersection number of
, the algebraic intersection number of 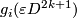 and
and  is zero.
Applying item 2 of Lemma6.3 to
is zero.
Applying item 2 of Lemma6.3 to 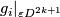 as
as  , embedding of
, embedding of  into
into 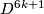 as
as  and
and 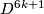 as
as  we may suppose that
we may suppose that 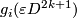 does not intersect
does not intersect  .
Hance for any
.
Hance for any  renamed by
renamed by 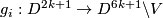 a map which coincides with
a map which coincides with 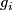 on
on 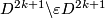 and
and 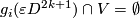 .
.
???Denote by 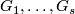 the maps as in Lemma 6.5 for
the maps as in Lemma 6.5 for  and
and 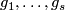 as described above.
Denote by
as described above.
Denote by 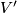 the manifold as in Lemma 6.6.
Since
the manifold as in Lemma 6.6.
Since 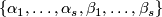 is a basis in
is a basis in 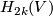 , ???it follows that
, ???it follows that 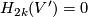 .
Since
.
Since 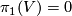 we have
we have 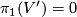 .
Hence???
.
Hence??? 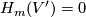 for
for  .
From Generalized Poincare conjecture proved by Smale it follows that
.
From Generalized Poincare conjecture proved by Smale it follows that 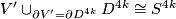 .
Hence
.
Hence 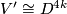 .
Then we set by???
.
Then we set by???  a ???diffeomorphism between
a ???diffeomorphism between 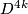 and
and 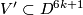 such that
such that 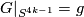 .
.

References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Ha62] Template:Ha62
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 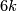 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Pontryagin1959] L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, Amer. Math. Soc. Translations, Ser. 2, Vol. 11, Providence, R.I. (1959), 1–114. MR0115178 (22 #5980) Zbl 0084.19002
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021