Stiefel-Whitney characteristic classes
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a compact smooth
be a compact smooth  -manifold (possibly with boundary).
Denote by
-manifold (possibly with boundary).
Denote by 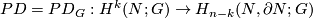 the Poincaré duality isomorphism.
Here for non-orientable
the Poincaré duality isomorphism.
Here for non-orientable  the coefficients in cohomology are twisted (by the orientation double covering) and the coefficients in homology are non-twisted.
Let
the coefficients in cohomology are twisted (by the orientation double covering) and the coefficients in homology are non-twisted.
Let 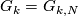 be
be  if either
if either 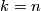 or
or  is odd, and
is odd, and  if either
if either 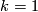 or
or  is even.
is even.
Stiefel defined the homology Stiefel-Whitney class 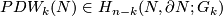 of
of  to be the homology class of a degeneracy subset of a general position collection of
to be the homology class of a degeneracy subset of a general position collection of 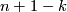 tangent vector fields on
tangent vector fields on  . Let
. Let 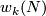 be the reduction of
be the reduction of 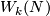 modulo 2.
modulo 2.
Whitney defined the homology normal Stiefel-Whitney class 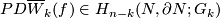 of
of  to be the homology class of a degeneracy subset of a general position collection of
to be the homology class of a degeneracy subset of a general position collection of 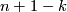 normal vector fields on an immersion
normal vector fields on an immersion 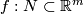 .
By the Whitney-Wu formula 2.1 the reduction modulo 2 of this class (but not this class itself!) is independent of
.
By the Whitney-Wu formula 2.1 the reduction modulo 2 of this class (but not this class itself!) is independent of  and depends only on
and depends only on  .
So this reduction is denoted by
.
So this reduction is denoted by 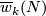 .
.
Let ![w_0(N)=\overline w_0(N)=[N]](/images/math/8/7/4/874e8a8d6533883a2bdaf04e70bf9ad8.png) .
.
See details e.g. in [Milnor&Stasheff1974,  12], [Fomenko&Fuchs2016,
12], [Fomenko&Fuchs2016,  19.C], [Skopenkov2015b,
19.C], [Skopenkov2015b,  9,11,12].
9,11,12].
There is an alternative definition of 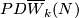 [Skopenkov2006,
[Skopenkov2006,  2.3 `the Whitney obstruction'] analogous to definition of the Whitney invariant.
2.3 `the Whitney obstruction'] analogous to definition of the Whitney invariant.
See also Wikipedia article.
2 Whitney-Wu formula
In this section we abbreviate 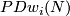 to just
to just 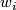 and
and 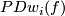 to just
to just 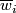 .
.
Theorem 2.1 (Whitney-Wu formula).
If is a closed smooth
is a closed smooth  -manifold,
-manifold, 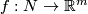 an immersion and
an immersion and 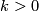 is an integer, then
is an integer, then 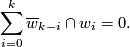
Proof. (This proof should be known but is absent from textbooks. This text is written by M. Fedorov and A. Skopenkov in frame of the course `Algebraic topology of manifolds in interesting results'.)
Denote by 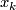 the obstruction to existence of
the obstruction to existence of 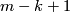 linearly independent fields on
linearly independent fields on  .
Clearly
.
Clearly 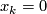 .
So it suffices to show that
.
So it suffices to show that 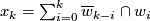 .
.
Take a general position collection of normal fields 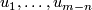 on
on  such that for each
such that for each 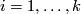 the collection
the collection 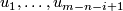 is linearly dependent on some
is linearly dependent on some 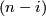 -subcomplex
-subcomplex 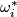 representing
representing 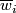 .
.
Take a general position collection of tangent fields 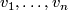 on
on  such that for each
such that for each 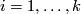 the collection
the collection 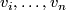 is linearly dependent on some
is linearly dependent on some 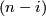 -subcomplex
-subcomplex 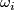 representing
representing 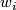 .
.
Define 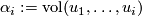 and
and 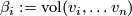 .
Denote by
.
Denote by 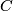 the following collection of
the following collection of 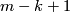 vector fields on
vector fields on  :
:
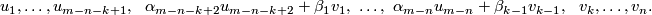
This is a general position collection, so 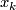 is represented by the set set on which
is represented by the set set on which 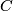 is linearly dependent. Clearly, all non-zero vectors among
is linearly dependent. Clearly, all non-zero vectors among
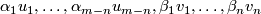 are linearly independent. Hence
are linearly independent. Hence 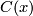 is linearly dependent if and only if either:
is linearly dependent if and only if either:
*are linearly dependent at
(which happens on
) or *
are linearly dependent at
(which happens on
) or *
contains a zero vector (which happens if and only if
at
for some
).
Thus 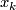 is represented by
is represented by 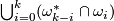 , where
, where 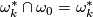 and
and 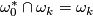
3 References
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2015b] A. Skopenkov, Algebraic Topology From Geometric Viewpoint (in Russian), MCCME, Moscow, 2015, 2020. Preprint of a part in English