Knots, i.e. embeddings of spheres
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
See general introduction on embeddings, notation and conventions in [Skopenkov2016c,  1,
1,  3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for  one constructs a smooth embedding
one constructs a smooth embedding 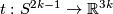 .
For
.
For  even this embedding is a generator of
even this embedding is a generator of 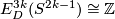 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 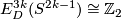 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 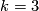 .
.
3 Classification
Theorem 3.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 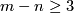 the group
the group  is finite unless
is finite unless 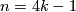 and
and 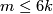 , when
, when  is the sum of
is the sum of 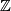 and a finite group.
and a finite group.
Theorem 3.2 (Haefliger-Milgram).
We have the following table for the group  ; in the table
; in the table 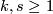 :
:
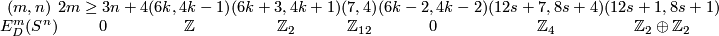
Proof for the first four columns, and for the fifth column,  even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,
even, are presented in [Haefliger1966] (or are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case
3]).
The remaining results were announced in [Milgram1972]; no details of the proofs appeared.
Alternative proofs for the case 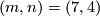 are given in [Skopenkov2005], [Crowley&Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008].
Theorem 3.3 [Milgram1972, Corollary G].
We have 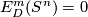 if and only if either
if and only if either 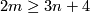 , or
, or 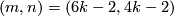 , or
, or 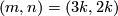 and
and 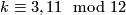 , or
, or 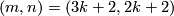 and
and 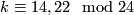 .
.
For readily calculable description of 2-components of  see [Milgram1972, Theorem F].
see [Milgram1972, Theorem F].
For  the group
the group  has been described in terms of exact sequences involving the homotopy groups of spheres and of the pairs
has been described in terms of exact sequences involving the homotopy groups of spheres and of the pairs 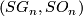 [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Here
[Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Here 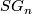 is the space of maps
is the space of maps 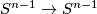 of degree
of degree  .
Restricting an element of
.
Restricting an element of 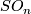 to
to 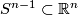 identifies
identifies 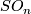 as a subspace of
as a subspace of 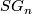 .
.
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 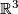 ), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
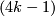 -spheres in
-spheres in 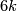 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.