Knots, i.e. embeddings of spheres
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
We work in a smooth category. In particular, terms embedding and smooth embedding or map and smooth map are used interchangeably. For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
2 Examples
There are smooth embeddings 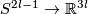 which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
Example 2.1. (a) Analogously to the Haefliger trefoil knot for any  one constructs a smooth embedding
one constructs a smooth embedding 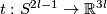 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even
even  is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding;  represents a generator of
represents a generator of 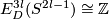 [Haefliger1962].
[Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 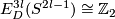 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 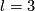 .
.
(b) For any 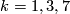 let
let 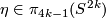 be the homotopy class of the Hopf map.
Denote by
be the homotopy class of the Hopf map.
Denote by 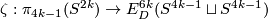 the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum
the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum 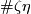 of the components of (a representative of)
of the components of (a representative of) 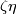 is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding; 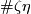 is a generator of
is a generator of 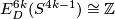 [Skopenkov2015a, Corollary 2.13].
[Skopenkov2015a, Corollary 2.13].
3 Invariants
Let us define the Haefliger invariant 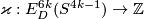 .
The definition is motivated by Haefliger's proof that any embedding
.
The definition is motivated by Haefliger's proof that any embedding 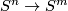 is isotopic to the standard embedding for
is isotopic to the standard embedding for  , and by analyzing what obstructs carrying this proof for
, and by analyzing what obstructs carrying this proof for  .
.
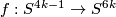 has a framing extendable to a framed embedding
has a framing extendable to a framed embedding 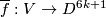 of a
of a  -manifold
-manifold  whose boundary is
whose boundary is 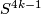 , and whose signature is zero. For an integer
, and whose signature is zero. For an integer 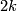 -cycle
-cycle  in
in  let
let 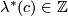 be the linking number of
be the linking number of 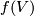 with a slight shift of
with a slight shift of 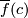 along the first vector of the framing. This defines a map
along the first vector of the framing. This defines a map 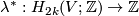 . This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique
. This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique 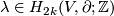 such that
such that ![\lambda^*[c]=\lambda\cap_V[c]](/images/math/b/2/8/b2878e69f979f9a0ca580faf4d104941.png) for any
for any ![[c]\in H_{2k}(V;\Z)](/images/math/8/9/f/89f1bbfc9e8e5259c8e842991bb8018b.png) . Since
. Since  has a normal framing, its intersection form
has a normal framing, its intersection form 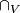 is even. (Indeed, represent a class in
is even. (Indeed, represent a class in 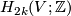 by a closed oriented
by a closed oriented 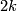 -submanifold
-submanifold  . Then
. Then ![\rho_2[c]\cap_V[c]=\overline{w_{2k}}(c\subset V)=\rho_2[c]\cap_VPDw_{2k}(V)=0](/images/math/7/8/8/788a4e3686035885f1e93cfe29a761c1.png) because
because  has a normal framing.) Hence
has a normal framing.) Hence 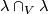 is an even integer. Define
is an even integer. Define 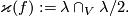
Since the signature of  is zero, there is a symplectic basis
is zero, there is a symplectic basis  in
in  .
Then clearly
.
Then clearly
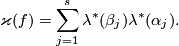
For an alternative definition via Seifert surfaces in 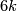 -space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,
-space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,  4].
4].
Sketch of a proof that 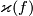 is well-defined (i.e. is independent of
is well-defined (i.e. is independent of  ,
, 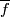 , and the framings), and is invariant under isotopy of
, and the framings), and is invariant under isotopy of  . [Haefliger1962, Theorem 2.6]
Analogously one defines
. [Haefliger1962, Theorem 2.6]
Analogously one defines 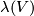 and
and 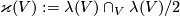 for a framed
for a framed  -submanifold
-submanifold  of
of  . Since
. Since 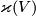 is a characteristic number, it is independent of framed cobordism. So
is a characteristic number, it is independent of framed cobordism. So 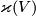 defines a homomorphism
defines a homomorphism 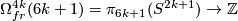 . The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
. The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
Since 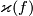 is a characteristic number, it is independent of framed cobordism of a framed
is a characteristic number, it is independent of framed cobordism of a framed  (and hence of the isotopy of a framed
(and hence of the isotopy of a framed  ).
).
Therefore 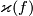 is a well-defined invariant of a framed cobordism class of a framed
is a well-defined invariant of a framed cobordism class of a framed  . By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3])
. By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3]) 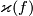 is also independent of the framing of
is also independent of the framing of  extendable to a framing of some
extendable to a framing of some  -manifold
-manifold  having trivial signature. QED
having trivial signature. QED
For definition of the attaching invariant 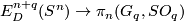 see [Haefliger1966], [Skopenkov2005,
see [Haefliger1966], [Skopenkov2005,  3].
3].
4 Classification
Theorem 4.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 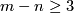 the group
the group  is finite unless
is finite unless 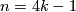 and
and 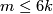 , when
, when  is the sum of
is the sum of 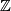 and a finite group.
and a finite group.
Theorem 4.2 (Haefliger-Milgram).
We have the following table for the group  ; in the whole table
; in the whole table 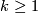 ; in the fifth column
; in the fifth column 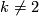 ; in the last two columns
; in the last two columns 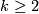 :
:
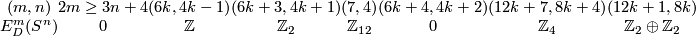
Proof for the first four columns, and for the fifth column when  is odd, are presented in [Haefliger1966, 8.15] (see also
is odd, are presented in [Haefliger1966, 8.15] (see also  6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,
6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]; there is a typo in [Haefliger1966, 8.15]:
3]; there is a typo in [Haefliger1966, 8.15]: 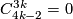 should be
should be 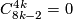 ). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases
). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases 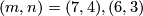 are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
Theorem 4.3 [Milgram1972, Corollary G].
We have 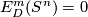 if and only if either
if and only if either 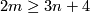 , or
, or 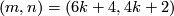 ,
or
,
or 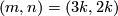 and
and 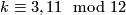 ,
or
,
or 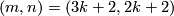 and
and 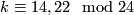 .
.
For a description of 2-components of  see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
The lowest-dimensional unknown groups  are
are 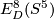 and
and 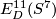 .
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
.
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 4.4 [Haefliger1966].
For 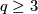 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
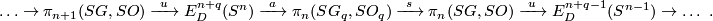
Here 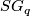 is the space of maps
is the space of maps 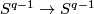 of degree
of degree  . Restricting a map from
. Restricting a map from 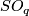 to
to 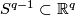 identifies
identifies 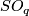 as a subspace of
as a subspace of 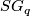 . Define
. Define 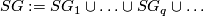 . Analogously define
. Analogously define 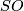 . Let
. Let  be the stabilization homomorphism. The attaching invariant
be the stabilization homomorphism. The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
5 Some remarks on codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 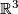 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
6 Proof of classification of (4k-1)-knots in 6k-space
Theorem 6.1.
The Haefliger invariant 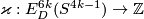 is injective for
is injective for  .
.
The proof is a certain simplification of [Haefliger1962]. We present an exposition structured to make it more accessible to non-specialists.
Lemma 6.2.
Let  be a framed
be a framed 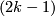 -connected
-connected  -submanifold of
-submanifold of 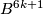 such that
such that 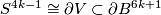 , signature of
, signature of  is zero, and
is zero, and 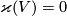 .
Then there is a submanifold
.
Then there is a submanifold 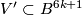 such that
such that 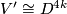 and
and 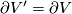 .
.
Proof of Theorem 6.1 using Lemma 6.2.
By the first three paragraphs of the proof of Theorem 3.1 in [Haefliger1962], for any embedding 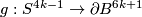 such that
such that 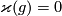 there is a framed
there is a framed 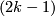 -connected
-connected  -submanifold
-submanifold  of
of 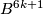 with zero signature such that
with zero signature such that 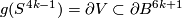 and
and 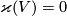 .
Then by Lemma 6.2 there is a submanifold
.
Then by Lemma 6.2 there is a submanifold 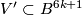 such that
such that 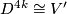 and
and 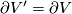 .
Recall that isotopy classes of embeddings
.
Recall that isotopy classes of embeddings 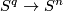 are in 1--1 correspondence with
are in 1--1 correspondence with  -cobordism classes of oriented submanifolds of
-cobordism classes of oriented submanifolds of  diffeomorphic to
diffeomorphic to 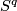 for
for 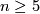 ,
, 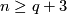 , cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence
, cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence  is isotopic to standart embedding.
is isotopic to standart embedding. 
To prove Lemma 6.2 we need Lemmas 6.3, 6.4 and 6.5. Below manifolds can have non-empty boundaries.
Lemma 6.3 [Whitney lemma; [Prasolov2007],  22].
Let
22].
Let 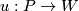 be a map from a connected oriented
be a map from a connected oriented  -manifold
-manifold  to a simply connected oriented
to a simply connected oriented 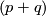 -manifold
-manifold  . If
. If 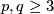 , then
, then
- If
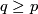 , there is a homotopy
, there is a homotopy 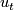 such that
such that 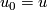 and
and 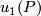 is an embedding.
is an embedding.
- Suppose in addition that
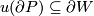 and there is a map
and there is a map 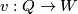 with
with 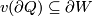 from a connected oriented
from a connected oriented  -manifold
-manifold 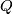 such that the algebraic intersection number of
such that the algebraic intersection number of 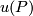 and
and 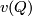 is zero. Then there is a homotopy
is zero. Then there is a homotopy 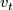 relative to the boundary such that
relative to the boundary such that 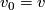 and
and 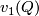 does not intersect
does not intersect 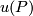 . If
. If  is an embedding, the homotopy
is an embedding, the homotopy 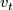 can be chosen so that
can be chosen so that 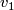 is an embedding.
is an embedding.
Below we denote by 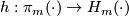 the Hurewicz map.
the Hurewicz map.
Lemma 6.4. Let  be a
be a 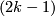 -connected
-connected  -manifold, and let
-manifold, and let 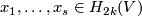 be homology classes such that
be homology classes such that 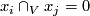 for every
for every 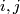 .
Then there are embeddings
.
Then there are embeddings 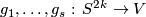 with pairwise disjoint images representing
with pairwise disjoint images representing 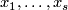 , respectively.
, respectively.
Proof. As  is
is 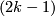 -connected,
-connected, 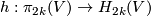 is an isomorphism.
For an element
is an isomorphism.
For an element 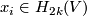 , let
, let 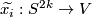 be a representative of the homotopy class
be a representative of the homotopy class 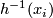 .
Applying item 1 of Lemma 6.3 to
.
Applying item 1 of Lemma 6.3 to 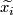 , we may assume that
, we may assume that 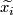 is an embedding.
is an embedding.
Make the following inductive procedure.
At the  -th step,
-th step, 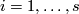 , assume that the embeddings
, assume that the embeddings 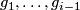 are already constructed, and we construct
are already constructed, and we construct 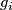 .
Since
.
Since 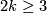 and
and  is simply connected,
is simply connected, 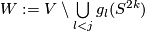 is simply connected for any
is simply connected for any 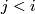 .
The algebraic intersection number of
.
The algebraic intersection number of 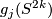 and
and 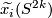 is zero for any
is zero for any  .
Hence we can apply item 2 of Lemma 6.3 to
.
Hence we can apply item 2 of Lemma 6.3 to 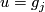 and
and 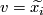 and
and  as above for any
as above for any 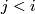 .
So
.
So 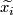 is replaced by a homotopic embedding
is replaced by a homotopic embedding 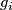 , and the images of
, and the images of 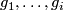 are pairwise disjoint.
After
are pairwise disjoint.
After  -th step we obtain a required set of embeddings.
-th step we obtain a required set of embeddings.

Lemma 6.5.
Let  be an orientable
be an orientable  -submanifold of
-submanifold of 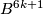 , and
, and 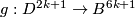 be an embedding such that
be an embedding such that 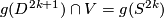 and over
and over  the manifold
the manifold  has a framing whose first vector is tangent to
has a framing whose first vector is tangent to 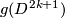 .
Assume that
.
Assume that  has zero algebraic self-intersection in
has zero algebraic self-intersection in  .
Then
.
Then  extends to an embedding
extends to an embedding 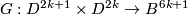 such that
such that 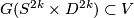 .
.
Proof. (A slightly different proof is presented in the proof of Proposition 3.3 in [Haefliger1962].)
Since  has zero algebraic self-intersection in
has zero algebraic self-intersection in  , the Euler class of the normal bundle of
, the Euler class of the normal bundle of  in
in  is zero.
Since over
is zero.
Since over  the manifold
the manifold  has a framing, we obtain that
has a framing, we obtain that  has a framing in
has a framing in  .
.
Identify all the normal spaces of 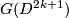 with the normal space at
with the normal space at 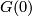 .
The normal framing
.
The normal framing  of
of  in
in  is orthogonal to
is orthogonal to 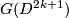 .
So
.
So  defines a map
defines a map 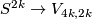 .
Let
.
Let 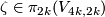 be the homotopy class of this map.
This is the obstruction to extending
be the homotopy class of this map.
This is the obstruction to extending  to a normal
to a normal 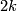 -framing of
-framing of  in
in 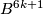 (so apriori
(so apriori 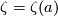 ).
It suffices to prove that
).
It suffices to prove that 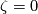 .
.
Consider the exact sequence of the bundle 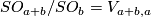 :
:
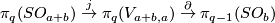 .
By the following well-known assertion,
.
By the following well-known assertion, 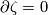 :
if
:
if 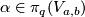 , then
, then 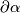 is the obstruction to trivialization of the orthogonal complement to the field of
is the obstruction to trivialization of the orthogonal complement to the field of  -frames in
-frames in 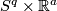 corresponding to a representative of
corresponding to a representative of  .
.
Consider a map of the exact sequences associated to the inclusion 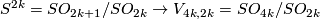 .
The composition
.
The composition 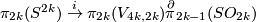 is the boundary map
is the boundary map 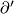 .
The group
.
The group 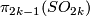 is in natural 1--1 correspondence with
is in natural 1--1 correspondence with 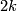 -bundles over
-bundles over 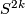 .
The image
.
The image 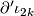 is the tangent bundle
is the tangent bundle  of
of 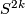 .
Since the Euler class of
.
Since the Euler class of 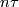 is
is 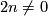 , the map
, the map 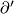 is injective.
is injective.
Alternatively, by [Fomenko&Fuchs2016, Corollary in  25.4]
25.4] 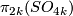 is a finite group (in [Fomenko&Fuchs2016, Corollary in
is a finite group (in [Fomenko&Fuchs2016, Corollary in  25.4] the formula for
25.4] the formula for 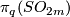 is correct, although the formula for
is correct, although the formula for 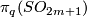 is incorrect because
is incorrect because 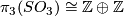 ).
Since
).
Since 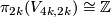 , we obtain that
, we obtain that 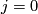 for
for 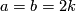 .
This and
.
This and 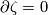 imply that
imply that 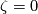 .
.

Lemma 6.6.
Let  be a
be a  -submanifold of
-submanifold of 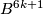 and let
and let 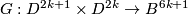 be an embedding such that
be an embedding such that 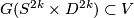 .
Then there is a smooth submanifold
.
Then there is a smooth submanifold 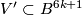 homeomorphic to
homeomorphic to 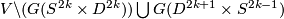 and such that
and such that 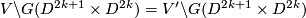 .
.
Lemma 6.6 is essentialy proved in [Haefliger1962,  3.3].
3.3].
Proof of Lemma 6.2 using Lemmas 6.4, 6.5.
By the fourth paragraph of the proof of Theorem 3.1 in [Haefliger1962], there is a basis 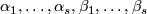 in
in 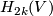 such that
such that 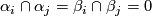 ,
, 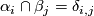 and
and 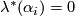 for any
for any 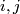 .
From Lemma 6.4 it follows that there are embeddings
.
From Lemma 6.4 it follows that there are embeddings 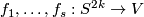 with pairwise disjoint images representing
with pairwise disjoint images representing 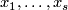 , respectively.
[!!!such that
, respectively.
[!!!such that ![f_{i*}[S^{2k}]=\alpha_i](/images/math/3/b/2/3b268affe6aabac0a3606326baf06b92.png) for every
for every 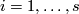 ]
]
For 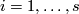 denote by
denote by 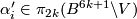 the homotopy class of the shift of
the homotopy class of the shift of 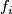 by the first vector of the framing of
by the first vector of the framing of  on
on 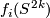 .
Since
.
Since 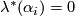 , we have
, we have 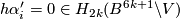 .
Since
.
Since 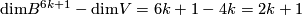 , the complement
, the complement 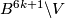 is
is 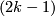 -connected.
Hence by Hurewicz Theorem
-connected.
Hence by Hurewicz Theorem 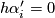 implies
implies 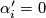 .
Therefore there are extensions
.
Therefore there are extensions 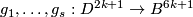 of
of 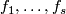 such that
such that 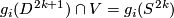 .
.
Take  such that
such that 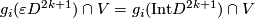 for any
for any 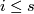 .
Take a tubular neighborhoods
.
Take a tubular neighborhoods 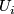 of
of 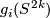 such that
such that 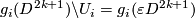 for any
for any 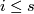 .
The algebraic intersection number of
.
The algebraic intersection number of 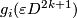 and
and 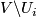 equals
equals ![\lambda^*(\alpha_i)=\lambda^*(g_{i*}[S^{2k}])=0](/images/math/7/4/2/7421b0739b5cce6ae14a3247ea7ab1fc.png) .
We have
.
We have 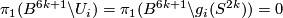 .
So we can apply item 2 of Lemma 6.3 to
.
So we can apply item 2 of Lemma 6.3 to 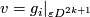 ,
, 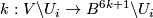 the inclusion, and
the inclusion, and 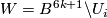 .
So we may assume that
.
So we may assume that 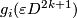 does not intersect
does not intersect 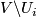 .
Hence we may assume that
.
Hence we may assume that 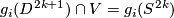 .
.
Apply Lemma 6.5 to 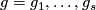 one by one, and to the manifold
one by one, and to the manifold  .
Denote by
.
Denote by 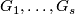 the resulting maps.
Define manifolds
the resulting maps.
Define manifolds 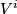 for
for 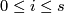 inductively.
Let
inductively.
Let 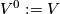 , and let
, and let 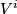 be a manifold
be a manifold 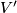 obtained applying Lemma 6.6 for
obtained applying Lemma 6.6 for 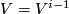 and
and 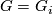 .
By Lemma 6.6,
.
By Lemma 6.6, 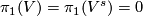 and
and 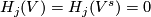 for
for 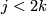 .
Since
.
Since 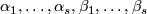 is a symplectic basis in
is a symplectic basis in 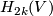 , it follows that
, it follows that 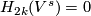 .
Then from Generalized Poincare conjecture proved by Smale it follows that
.
Then from Generalized Poincare conjecture proved by Smale it follows that 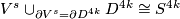 .
Hence
.
Hence 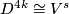 .
Then take
.
Then take 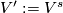 .
.

References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
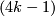 -spheres in
-spheres in 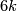 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Kervaire1965] M. A. Kervaire, Les noeuds de dimensions sup'erieures, Bull. Soc. Math. France 93 (1965), 225-271.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Pontryagin1959] L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, Amer. Math. Soc. Translations, Ser. 2, Vol. 11, Providence, R.I. (1959), 1–114. MR0115178 (22 #5980) Zbl 0084.19002
- [Prasolov2007] V. V. Prasolov, Elements of homology theory, American Mathematical Society, 2007. MR2313004 (2008d:55001) Zbl 1120.55001
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
 3].
3].
2 Examples
There are smooth embeddings 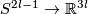 which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
Example 2.1. (a) Analogously to the Haefliger trefoil knot for any  one constructs a smooth embedding
one constructs a smooth embedding 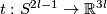 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even
even  is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding;  represents a generator of
represents a generator of 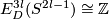 [Haefliger1962].
[Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 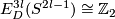 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 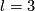 .
.
(b) For any 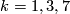 let
let 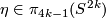 be the homotopy class of the Hopf map.
Denote by
be the homotopy class of the Hopf map.
Denote by 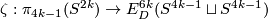 the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum
the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum 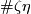 of the components of (a representative of)
of the components of (a representative of) 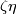 is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding; 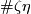 is a generator of
is a generator of 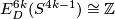 [Skopenkov2015a, Corollary 2.13].
[Skopenkov2015a, Corollary 2.13].
3 Invariants
Let us define the Haefliger invariant 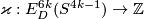 .
The definition is motivated by Haefliger's proof that any embedding
.
The definition is motivated by Haefliger's proof that any embedding 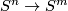 is isotopic to the standard embedding for
is isotopic to the standard embedding for 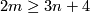 , and by analyzing what obstructs carrying this proof for
, and by analyzing what obstructs carrying this proof for 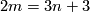 .
.
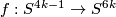 has a framing extendable to a framed embedding
has a framing extendable to a framed embedding 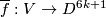 of a
of a  -manifold
-manifold  whose boundary is
whose boundary is 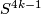 , and whose signature is zero. For an integer
, and whose signature is zero. For an integer 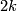 -cycle
-cycle  in
in  let
let 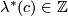 be the linking number of
be the linking number of 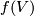 with a slight shift of
with a slight shift of 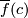 along the first vector of the framing. This defines a map
along the first vector of the framing. This defines a map 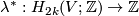 . This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique
. This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique 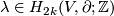 such that
such that ![\lambda^*[c]=\lambda\cap_V[c]](/images/math/b/2/8/b2878e69f979f9a0ca580faf4d104941.png) for any
for any ![[c]\in H_{2k}(V;\Z)](/images/math/8/9/f/89f1bbfc9e8e5259c8e842991bb8018b.png) . Since
. Since  has a normal framing, its intersection form
has a normal framing, its intersection form 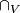 is even. (Indeed, represent a class in
is even. (Indeed, represent a class in 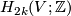 by a closed oriented
by a closed oriented 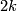 -submanifold
-submanifold  . Then
. Then ![\rho_2[c]\cap_V[c]=\overline{w_{2k}}(c\subset V)=\rho_2[c]\cap_VPDw_{2k}(V)=0](/images/math/7/8/8/788a4e3686035885f1e93cfe29a761c1.png) because
because  has a normal framing.) Hence
has a normal framing.) Hence 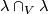 is an even integer. Define
is an even integer. Define 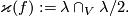
Since the signature of  is zero, there is a symplectic basis
is zero, there is a symplectic basis 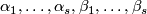 in
in 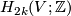 .
Then clearly
.
Then clearly
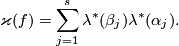
For an alternative definition via Seifert surfaces in  -space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,
-space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,  4].
4].
Sketch of a proof that 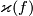 is well-defined (i.e. is independent of
is well-defined (i.e. is independent of  ,
, 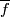 , and the framings), and is invariant under isotopy of
, and the framings), and is invariant under isotopy of  . [Haefliger1962, Theorem 2.6]
Analogously one defines
. [Haefliger1962, Theorem 2.6]
Analogously one defines 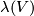 and
and 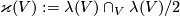 for a framed
for a framed  -submanifold
-submanifold  of
of 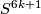 . Since
. Since 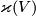 is a characteristic number, it is independent of framed cobordism. So
is a characteristic number, it is independent of framed cobordism. So 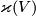 defines a homomorphism
defines a homomorphism 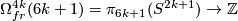 . The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
. The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
Since 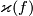 is a characteristic number, it is independent of framed cobordism of a framed
is a characteristic number, it is independent of framed cobordism of a framed  (and hence of the isotopy of a framed
(and hence of the isotopy of a framed  ).
).
Therefore 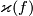 is a well-defined invariant of a framed cobordism class of a framed
is a well-defined invariant of a framed cobordism class of a framed  . By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3])
. By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3]) 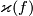 is also independent of the framing of
is also independent of the framing of  extendable to a framing of some
extendable to a framing of some  -manifold
-manifold  having trivial signature. QED
having trivial signature. QED
For definition of the attaching invariant 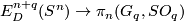 see [Haefliger1966], [Skopenkov2005,
see [Haefliger1966], [Skopenkov2005,  3].
3].
4 Classification
Theorem 4.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 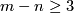 the group
the group  is finite unless
is finite unless 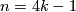 and
and 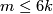 , when
, when  is the sum of
is the sum of 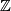 and a finite group.
and a finite group.
Theorem 4.2 (Haefliger-Milgram).
We have the following table for the group  ; in the whole table
; in the whole table 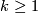 ; in the fifth column
; in the fifth column 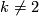 ; in the last two columns
; in the last two columns 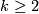 :
:
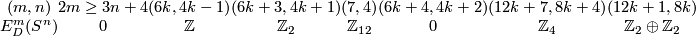
Proof for the first four columns, and for the fifth column when  is odd, are presented in [Haefliger1966, 8.15] (see also
is odd, are presented in [Haefliger1966, 8.15] (see also  6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,
6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]; there is a typo in [Haefliger1966, 8.15]:
3]; there is a typo in [Haefliger1966, 8.15]: 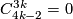 should be
should be 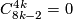 ). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases
). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases 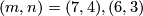 are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
Theorem 4.3 [Milgram1972, Corollary G].
We have 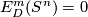 if and only if either
if and only if either 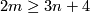 , or
, or 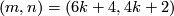 ,
or
,
or 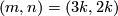 and
and 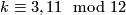 ,
or
,
or 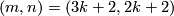 and
and 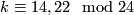 .
.
For a description of 2-components of  see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
The lowest-dimensional unknown groups  are
are 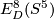 and
and 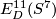 .
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
.
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 4.4 [Haefliger1966].
For 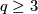 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
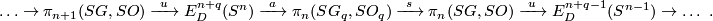
Here 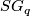 is the space of maps
is the space of maps 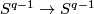 of degree
of degree  . Restricting a map from
. Restricting a map from 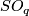 to
to 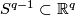 identifies
identifies 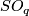 as a subspace of
as a subspace of 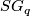 . Define
. Define 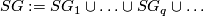 . Analogously define
. Analogously define 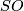 . Let
. Let  be the stabilization homomorphism. The attaching invariant
be the stabilization homomorphism. The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
5 Some remarks on codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 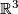 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
6 Proof of classification of (4k-1)-knots in 6k-space
Theorem 6.1.
The Haefliger invariant 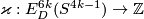 is injective for
is injective for  .
.
The proof is a certain simplification of [Haefliger1962]. We present an exposition structured to make it more accessible to non-specialists.
Lemma 6.2.
Let  be a framed
be a framed 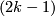 -connected
-connected  -submanifold of
-submanifold of 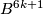 such that
such that 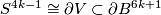 , signature of
, signature of  is zero, and
is zero, and 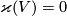 .
Then there is a submanifold
.
Then there is a submanifold 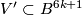 such that
such that 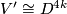 and
and 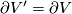 .
.
Proof of Theorem 6.1 using Lemma 6.2.
By the first three paragraphs of the proof of Theorem 3.1 in [Haefliger1962], for any embedding 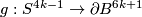 such that
such that 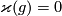 there is a framed
there is a framed 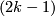 -connected
-connected  -submanifold
-submanifold  of
of 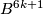 with zero signature such that
with zero signature such that 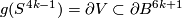 and
and 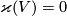 .
Then by Lemma 6.2 there is a submanifold
.
Then by Lemma 6.2 there is a submanifold 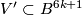 such that
such that 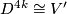 and
and 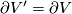 .
Recall that isotopy classes of embeddings
.
Recall that isotopy classes of embeddings 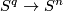 are in 1--1 correspondence with
are in 1--1 correspondence with  -cobordism classes of oriented submanifolds of
-cobordism classes of oriented submanifolds of  diffeomorphic to
diffeomorphic to 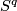 for
for 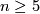 ,
, 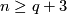 , cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence
, cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence  is isotopic to standart embedding.
is isotopic to standart embedding. 
To prove Lemma 6.2 we need Lemmas 6.3, 6.4 and 6.5. Below manifolds can have non-empty boundaries.
Lemma 6.3 [Whitney lemma; [Prasolov2007],  22].
Let
22].
Let 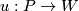 be a map from a connected oriented
be a map from a connected oriented  -manifold
-manifold  to a simply connected oriented
to a simply connected oriented 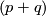 -manifold
-manifold  . If
. If 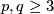 , then
, then
- If
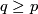 , there is a homotopy
, there is a homotopy 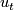 such that
such that 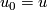 and
and 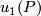 is an embedding.
is an embedding.
- Suppose in addition that
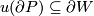 and there is a map
and there is a map 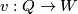 with
with 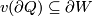 from a connected oriented
from a connected oriented  -manifold
-manifold 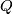 such that the algebraic intersection number of
such that the algebraic intersection number of 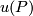 and
and 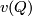 is zero. Then there is a homotopy
is zero. Then there is a homotopy 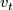 relative to the boundary such that
relative to the boundary such that 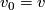 and
and 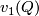 does not intersect
does not intersect 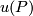 . If
. If  is an embedding, the homotopy
is an embedding, the homotopy 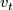 can be chosen so that
can be chosen so that 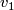 is an embedding.
is an embedding.
Below we denote by 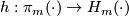 the Hurewicz map.
the Hurewicz map.
Lemma 6.4. Let  be a
be a 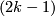 -connected
-connected  -manifold, and let
-manifold, and let 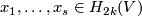 be homology classes such that
be homology classes such that 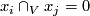 for every
for every 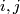 .
Then there are embeddings
.
Then there are embeddings 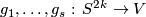 with pairwise disjoint images representing
with pairwise disjoint images representing 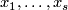 , respectively.
, respectively.
Proof. As  is
is 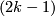 -connected,
-connected, 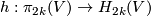 is an isomorphism.
For an element
is an isomorphism.
For an element 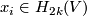 , let
, let 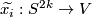 be a representative of the homotopy class
be a representative of the homotopy class 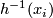 .
Applying item 1 of Lemma 6.3 to
.
Applying item 1 of Lemma 6.3 to 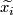 , we may assume that
, we may assume that 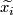 is an embedding.
is an embedding.
Make the following inductive procedure.
At the  -th step,
-th step, 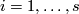 , assume that the embeddings
, assume that the embeddings 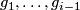 are already constructed, and we construct
are already constructed, and we construct 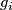 .
Since
.
Since 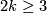 and
and  is simply connected,
is simply connected, 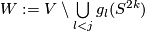 is simply connected for any
is simply connected for any 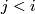 .
The algebraic intersection number of
.
The algebraic intersection number of 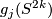 and
and 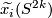 is zero for any
is zero for any  .
Hence we can apply item 2 of Lemma 6.3 to
.
Hence we can apply item 2 of Lemma 6.3 to 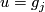 and
and 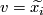 and
and  as above for any
as above for any 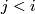 .
So
.
So 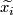 is replaced by a homotopic embedding
is replaced by a homotopic embedding 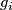 , and the images of
, and the images of 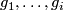 are pairwise disjoint.
After
are pairwise disjoint.
After  -th step we obtain a required set of embeddings.
-th step we obtain a required set of embeddings.

Lemma 6.5.
Let  be an orientable
be an orientable  -submanifold of
-submanifold of 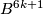 , and
, and 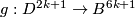 be an embedding such that
be an embedding such that 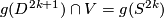 and over
and over  the manifold
the manifold  has a framing whose first vector is tangent to
has a framing whose first vector is tangent to 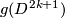 .
Assume that
.
Assume that  has zero algebraic self-intersection in
has zero algebraic self-intersection in  .
Then
.
Then  extends to an embedding
extends to an embedding 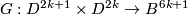 such that
such that 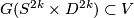 .
.
Proof. (A slightly different proof is presented in the proof of Proposition 3.3 in [Haefliger1962].)
Since  has zero algebraic self-intersection in
has zero algebraic self-intersection in  , the Euler class of the normal bundle of
, the Euler class of the normal bundle of  in
in  is zero.
Since over
is zero.
Since over  the manifold
the manifold  has a framing, we obtain that
has a framing, we obtain that  has a framing in
has a framing in  .
.
Identify all the normal spaces of 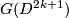 with the normal space at
with the normal space at 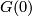 .
The normal framing
.
The normal framing  of
of  in
in  is orthogonal to
is orthogonal to 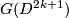 .
So
.
So  defines a map
defines a map 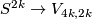 .
Let
.
Let 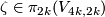 be the homotopy class of this map.
This is the obstruction to extending
be the homotopy class of this map.
This is the obstruction to extending  to a normal
to a normal 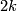 -framing of
-framing of  in
in 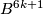 (so apriori
(so apriori 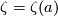 ).
It suffices to prove that
).
It suffices to prove that 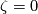 .
.
Consider the exact sequence of the bundle 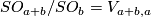 :
:
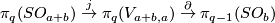 .
By the following well-known assertion,
.
By the following well-known assertion, 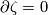 :
if
:
if 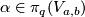 , then
, then 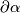 is the obstruction to trivialization of the orthogonal complement to the field of
is the obstruction to trivialization of the orthogonal complement to the field of  -frames in
-frames in 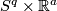 corresponding to a representative of
corresponding to a representative of  .
.
Consider a map of the exact sequences associated to the inclusion 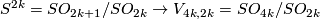 .
The composition
.
The composition 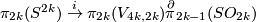 is the boundary map
is the boundary map 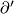 .
The group
.
The group 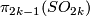 is in natural 1--1 correspondence with
is in natural 1--1 correspondence with 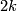 -bundles over
-bundles over 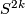 .
The image
.
The image 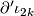 is the tangent bundle
is the tangent bundle  of
of 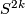 .
Since the Euler class of
.
Since the Euler class of 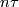 is
is 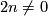 , the map
, the map 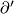 is injective.
is injective.
Alternatively, by [Fomenko&Fuchs2016, Corollary in  25.4]
25.4] 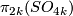 is a finite group (in [Fomenko&Fuchs2016, Corollary in
is a finite group (in [Fomenko&Fuchs2016, Corollary in  25.4] the formula for
25.4] the formula for 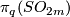 is correct, although the formula for
is correct, although the formula for 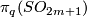 is incorrect because
is incorrect because 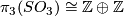 ).
Since
).
Since 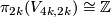 , we obtain that
, we obtain that 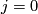 for
for 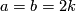 .
This and
.
This and 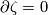 imply that
imply that 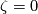 .
.

Lemma 6.6.
Let  be a
be a  -submanifold of
-submanifold of 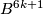 and let
and let 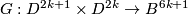 be an embedding such that
be an embedding such that 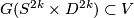 .
Then there is a smooth submanifold
.
Then there is a smooth submanifold 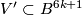 homeomorphic to
homeomorphic to 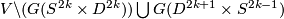 and such that
and such that 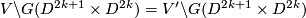 .
.
Lemma 6.6 is essentialy proved in [Haefliger1962,  3.3].
3.3].
Proof of Lemma 6.2 using Lemmas 6.4, 6.5.
By the fourth paragraph of the proof of Theorem 3.1 in [Haefliger1962], there is a basis 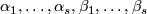 in
in 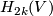 such that
such that 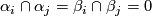 ,
, 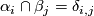 and
and 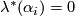 for any
for any 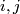 .
From Lemma 6.4 it follows that there are embeddings
.
From Lemma 6.4 it follows that there are embeddings 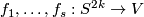 with pairwise disjoint images representing
with pairwise disjoint images representing 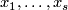 , respectively.
[!!!such that
, respectively.
[!!!such that ![f_{i*}[S^{2k}]=\alpha_i](/images/math/3/b/2/3b268affe6aabac0a3606326baf06b92.png) for every
for every 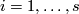 ]
]
For 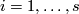 denote by
denote by 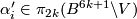 the homotopy class of the shift of
the homotopy class of the shift of 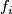 by the first vector of the framing of
by the first vector of the framing of  on
on 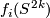 .
Since
.
Since 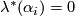 , we have
, we have 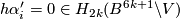 .
Since
.
Since 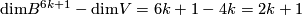 , the complement
, the complement 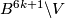 is
is 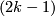 -connected.
Hence by Hurewicz Theorem
-connected.
Hence by Hurewicz Theorem 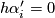 implies
implies 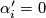 .
Therefore there are extensions
.
Therefore there are extensions 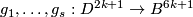 of
of 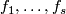 such that
such that 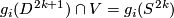 .
.
Take  such that
such that 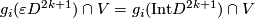 for any
for any 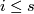 .
Take a tubular neighborhoods
.
Take a tubular neighborhoods 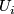 of
of 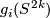 such that
such that 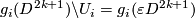 for any
for any 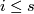 .
The algebraic intersection number of
.
The algebraic intersection number of 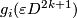 and
and 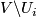 equals
equals ![\lambda^*(\alpha_i)=\lambda^*(g_{i*}[S^{2k}])=0](/images/math/7/4/2/7421b0739b5cce6ae14a3247ea7ab1fc.png) .
We have
.
We have 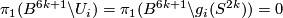 .
So we can apply item 2 of Lemma 6.3 to
.
So we can apply item 2 of Lemma 6.3 to 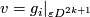 ,
, 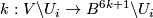 the inclusion, and
the inclusion, and 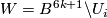 .
So we may assume that
.
So we may assume that 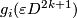 does not intersect
does not intersect 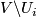 .
Hence we may assume that
.
Hence we may assume that 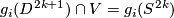 .
.
Apply Lemma 6.5 to 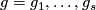 one by one, and to the manifold
one by one, and to the manifold  .
Denote by
.
Denote by 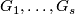 the resulting maps.
Define manifolds
the resulting maps.
Define manifolds 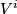 for
for 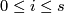 inductively.
Let
inductively.
Let 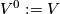 , and let
, and let 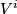 be a manifold
be a manifold 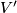 obtained applying Lemma 6.6 for
obtained applying Lemma 6.6 for 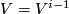 and
and 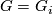 .
By Lemma 6.6,
.
By Lemma 6.6, 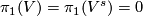 and
and 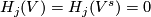 for
for 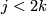 .
Since
.
Since 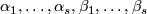 is a symplectic basis in
is a symplectic basis in 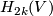 , it follows that
, it follows that 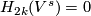 .
Then from Generalized Poincare conjecture proved by Smale it follows that
.
Then from Generalized Poincare conjecture proved by Smale it follows that 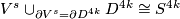 .
Hence
.
Hence 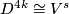 .
Then take
.
Then take 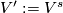 .
.

References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
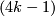 -spheres in
-spheres in 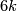 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Kervaire1965] M. A. Kervaire, Les noeuds de dimensions sup'erieures, Bull. Soc. Math. France 93 (1965), 225-271.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Pontryagin1959] L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, Amer. Math. Soc. Translations, Ser. 2, Vol. 11, Providence, R.I. (1959), 1–114. MR0115178 (22 #5980) Zbl 0084.19002
- [Prasolov2007] V. V. Prasolov, Elements of homology theory, American Mathematical Society, 2007. MR2313004 (2008d:55001) Zbl 1120.55001
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
 3].
3].
2 Examples
There are smooth embeddings 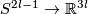 which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
Example 2.1. (a) Analogously to the Haefliger trefoil knot for any  one constructs a smooth embedding
one constructs a smooth embedding 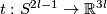 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even
even  is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding;  represents a generator of
represents a generator of 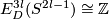 [Haefliger1962].
[Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 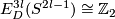 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 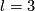 .
.
(b) For any 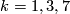 let
let 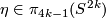 be the homotopy class of the Hopf map.
Denote by
be the homotopy class of the Hopf map.
Denote by 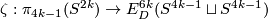 the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum
the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum 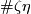 of the components of (a representative of)
of the components of (a representative of) 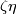 is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding; 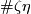 is a generator of
is a generator of 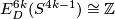 [Skopenkov2015a, Corollary 2.13].
[Skopenkov2015a, Corollary 2.13].
3 Invariants
Let us define the Haefliger invariant 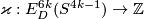 .
The definition is motivated by Haefliger's proof that any embedding
.
The definition is motivated by Haefliger's proof that any embedding 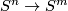 is isotopic to the standard embedding for
is isotopic to the standard embedding for 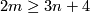 , and by analyzing what obstructs carrying this proof for
, and by analyzing what obstructs carrying this proof for 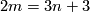 .
.
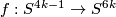 has a framing extendable to a framed embedding
has a framing extendable to a framed embedding 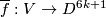 of a
of a  -manifold
-manifold  whose boundary is
whose boundary is 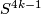 , and whose signature is zero. For an integer
, and whose signature is zero. For an integer 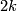 -cycle
-cycle  in
in  let
let 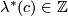 be the linking number of
be the linking number of 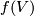 with a slight shift of
with a slight shift of 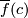 along the first vector of the framing. This defines a map
along the first vector of the framing. This defines a map 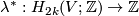 . This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique
. This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique 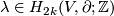 such that
such that ![\lambda^*[c]=\lambda\cap_V[c]](/images/math/b/2/8/b2878e69f979f9a0ca580faf4d104941.png) for any
for any ![[c]\in H_{2k}(V;\Z)](/images/math/8/9/f/89f1bbfc9e8e5259c8e842991bb8018b.png) . Since
. Since  has a normal framing, its intersection form
has a normal framing, its intersection form 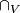 is even. (Indeed, represent a class in
is even. (Indeed, represent a class in 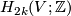 by a closed oriented
by a closed oriented 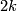 -submanifold
-submanifold  . Then
. Then ![\rho_2[c]\cap_V[c]=\overline{w_{2k}}(c\subset V)=\rho_2[c]\cap_VPDw_{2k}(V)=0](/images/math/7/8/8/788a4e3686035885f1e93cfe29a761c1.png) because
because  has a normal framing.) Hence
has a normal framing.) Hence 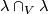 is an even integer. Define
is an even integer. Define 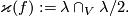
Since the signature of  is zero, there is a symplectic basis
is zero, there is a symplectic basis  in
in  .
Then clearly
.
Then clearly
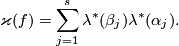
For an alternative definition via Seifert surfaces in 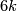 -space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,
-space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,  4].
4].
Sketch of a proof that 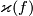 is well-defined (i.e. is independent of
is well-defined (i.e. is independent of  ,
, 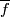 , and the framings), and is invariant under isotopy of
, and the framings), and is invariant under isotopy of  . [Haefliger1962, Theorem 2.6]
Analogously one defines
. [Haefliger1962, Theorem 2.6]
Analogously one defines 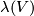 and
and 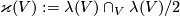 for a framed
for a framed  -submanifold
-submanifold  of
of 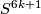 . Since
. Since 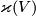 is a characteristic number, it is independent of framed cobordism. So
is a characteristic number, it is independent of framed cobordism. So 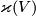 defines a homomorphism
defines a homomorphism 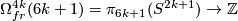 . The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
. The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
Since 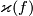 is a characteristic number, it is independent of framed cobordism of a framed
is a characteristic number, it is independent of framed cobordism of a framed  (and hence of the isotopy of a framed
(and hence of the isotopy of a framed  ).
).
Therefore 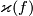 is a well-defined invariant of a framed cobordism class of a framed
is a well-defined invariant of a framed cobordism class of a framed  . By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3])
. By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3]) 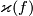 is also independent of the framing of
is also independent of the framing of  extendable to a framing of some
extendable to a framing of some  -manifold
-manifold  having trivial signature. QED
having trivial signature. QED
For definition of the attaching invariant 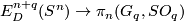 see [Haefliger1966], [Skopenkov2005,
see [Haefliger1966], [Skopenkov2005,  3].
3].
4 Classification
Theorem 4.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 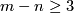 the group
the group  is finite unless
is finite unless 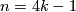 and
and 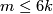 , when
, when  is the sum of
is the sum of 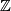 and a finite group.
and a finite group.
Theorem 4.2 (Haefliger-Milgram).
We have the following table for the group  ; in the whole table
; in the whole table 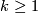 ; in the fifth column
; in the fifth column 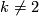 ; in the last two columns
; in the last two columns 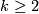 :
:
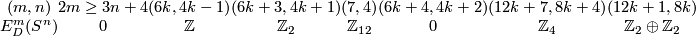
Proof for the first four columns, and for the fifth column when  is odd, are presented in [Haefliger1966, 8.15] (see also
is odd, are presented in [Haefliger1966, 8.15] (see also  6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,
6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]; there is a typo in [Haefliger1966, 8.15]:
3]; there is a typo in [Haefliger1966, 8.15]: 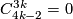 should be
should be 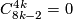 ). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases
). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases 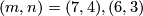 are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
Theorem 4.3 [Milgram1972, Corollary G].
We have 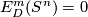 if and only if either
if and only if either 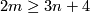 , or
, or 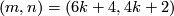 ,
or
,
or 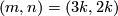 and
and 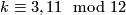 ,
or
,
or 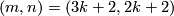 and
and 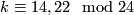 .
.
For a description of 2-components of  see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
The lowest-dimensional unknown groups  are
are 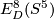 and
and 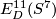 .
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
.
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 4.4 [Haefliger1966].
For 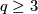 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
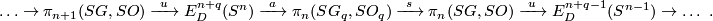
Here 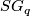 is the space of maps
is the space of maps 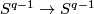 of degree
of degree  . Restricting a map from
. Restricting a map from 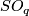 to
to 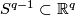 identifies
identifies 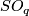 as a subspace of
as a subspace of 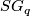 . Define
. Define 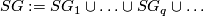 . Analogously define
. Analogously define 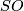 . Let
. Let  be the stabilization homomorphism. The attaching invariant
be the stabilization homomorphism. The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
5 Some remarks on codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 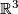 ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
6 Proof of classification of (4k-1)-knots in 6k-space
Theorem 6.1.
The Haefliger invariant 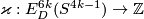 is injective for
is injective for  .
.
The proof is a certain simplification of [Haefliger1962]. We present an exposition structured to make it more accessible to non-specialists.
Lemma 6.2.
Let  be a framed
be a framed 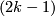 -connected
-connected  -submanifold of
-submanifold of 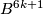 such that
such that 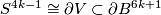 , signature of
, signature of  is zero, and
is zero, and 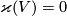 .
Then there is a submanifold
.
Then there is a submanifold 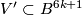 such that
such that 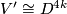 and
and 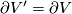 .
.
Proof of Theorem 6.1 using Lemma 6.2.
By the first three paragraphs of the proof of Theorem 3.1 in [Haefliger1962], for any embedding 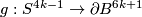 such that
such that 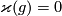 there is a framed
there is a framed 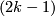 -connected
-connected  -submanifold
-submanifold  of
of 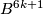 with zero signature such that
with zero signature such that 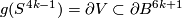 and
and 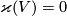 .
Then by Lemma 6.2 there is a submanifold
.
Then by Lemma 6.2 there is a submanifold 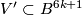 such that
such that 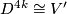 and
and 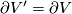 .
Recall that isotopy classes of embeddings
.
Recall that isotopy classes of embeddings 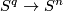 are in 1--1 correspondence with
are in 1--1 correspondence with  -cobordism classes of oriented submanifolds of
-cobordism classes of oriented submanifolds of  diffeomorphic to
diffeomorphic to 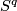 for
for 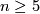 ,
, 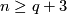 , cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence
, cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence  is isotopic to standart embedding.
is isotopic to standart embedding. 
To prove Lemma 6.2 we need Lemmas 6.3, 6.4 and 6.5. Below manifolds can have non-empty boundaries.
Lemma 6.3 [Whitney lemma; [Prasolov2007],  22].
Let
22].
Let 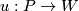 be a map from a connected oriented
be a map from a connected oriented  -manifold
-manifold  to a simply connected oriented
to a simply connected oriented 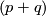 -manifold
-manifold  . If
. If 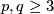 , then
, then
- If
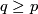 , there is a homotopy
, there is a homotopy 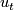 such that
such that 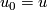 and
and 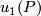 is an embedding.
is an embedding.
- Suppose in addition that
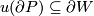 and there is a map
and there is a map 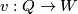 with
with 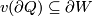 from a connected oriented
from a connected oriented  -manifold
-manifold 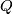 such that the algebraic intersection number of
such that the algebraic intersection number of 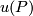 and
and 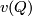 is zero. Then there is a homotopy
is zero. Then there is a homotopy 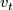 relative to the boundary such that
relative to the boundary such that 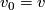 and
and 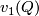 does not intersect
does not intersect 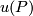 . If
. If  is an embedding, the homotopy
is an embedding, the homotopy 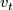 can be chosen so that
can be chosen so that 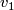 is an embedding.
is an embedding.
Below we denote by 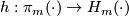 the Hurewicz map.
the Hurewicz map.
Lemma 6.4. Let  be a
be a 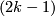 -connected
-connected  -manifold, and let
-manifold, and let 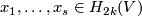 be homology classes such that
be homology classes such that 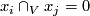 for every
for every 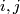 .
Then there are embeddings
.
Then there are embeddings 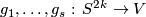 with pairwise disjoint images representing
with pairwise disjoint images representing 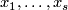 , respectively.
, respectively.
Proof. As  is
is 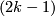 -connected,
-connected, 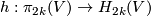 is an isomorphism.
For an element
is an isomorphism.
For an element 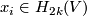 , let
, let 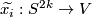 be a representative of the homotopy class
be a representative of the homotopy class 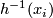 .
Applying item 1 of Lemma 6.3 to
.
Applying item 1 of Lemma 6.3 to 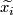 , we may assume that
, we may assume that 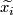 is an embedding.
is an embedding.
Make the following inductive procedure.
At the  -th step,
-th step, 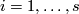 , assume that the embeddings
, assume that the embeddings 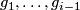 are already constructed, and we construct
are already constructed, and we construct 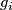 .
Since
.
Since 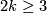 and
and  is simply connected,
is simply connected, 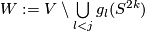 is simply connected for any
is simply connected for any 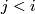 .
The algebraic intersection number of
.
The algebraic intersection number of 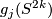 and
and 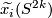 is zero for any
is zero for any  .
Hence we can apply item 2 of Lemma 6.3 to
.
Hence we can apply item 2 of Lemma 6.3 to 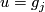 and
and 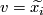 and
and  as above for any
as above for any 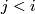 .
So
.
So 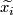 is replaced by a homotopic embedding
is replaced by a homotopic embedding 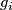 , and the images of
, and the images of 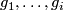 are pairwise disjoint.
After
are pairwise disjoint.
After  -th step we obtain a required set of embeddings.
-th step we obtain a required set of embeddings.

Lemma 6.5.
Let  be an orientable
be an orientable  -submanifold of
-submanifold of 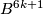 , and
, and 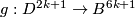 be an embedding such that
be an embedding such that 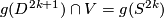 and over
and over  the manifold
the manifold  has a framing whose first vector is tangent to
has a framing whose first vector is tangent to 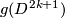 .
Assume that
.
Assume that  has zero algebraic self-intersection in
has zero algebraic self-intersection in  .
Then
.
Then  extends to an embedding
extends to an embedding 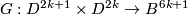 such that
such that 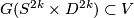 .
.
Proof. (A slightly different proof is presented in the proof of Proposition 3.3 in [Haefliger1962].)
Since  has zero algebraic self-intersection in
has zero algebraic self-intersection in  , the Euler class of the normal bundle of
, the Euler class of the normal bundle of  in
in  is zero.
Since over
is zero.
Since over  the manifold
the manifold  has a framing, we obtain that
has a framing, we obtain that  has a framing in
has a framing in  .
.
Identify all the normal spaces of 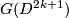 with the normal space at
with the normal space at 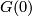 .
The normal framing
.
The normal framing  of
of  in
in  is orthogonal to
is orthogonal to 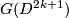 .
So
.
So  defines a map
defines a map 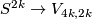 .
Let
.
Let 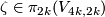 be the homotopy class of this map.
This is the obstruction to extending
be the homotopy class of this map.
This is the obstruction to extending  to a normal
to a normal 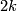 -framing of
-framing of  in
in 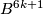 (so apriori
(so apriori 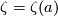 ).
It suffices to prove that
).
It suffices to prove that 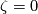 .
.
Consider the exact sequence of the bundle 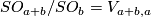 :
:
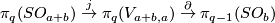 .
By the following well-known assertion,
.
By the following well-known assertion, 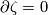 :
if
:
if 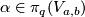 , then
, then 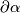 is the obstruction to trivialization of the orthogonal complement to the field of
is the obstruction to trivialization of the orthogonal complement to the field of  -frames in
-frames in 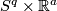 corresponding to a representative of
corresponding to a representative of  .
.
Consider a map of the exact sequences associated to the inclusion 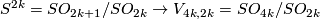 .
The composition
.
The composition 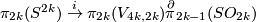 is the boundary map
is the boundary map 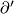 .
The group
.
The group 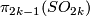 is in natural 1--1 correspondence with
is in natural 1--1 correspondence with 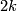 -bundles over
-bundles over 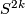 .
The image
.
The image 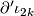 is the tangent bundle
is the tangent bundle  of
of 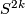 .
Since the Euler class of
.
Since the Euler class of 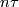 is
is 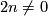 , the map
, the map 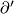 is injective.
is injective.
Alternatively, by [Fomenko&Fuchs2016, Corollary in  25.4]
25.4] 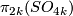 is a finite group (in [Fomenko&Fuchs2016, Corollary in
is a finite group (in [Fomenko&Fuchs2016, Corollary in  25.4] the formula for
25.4] the formula for 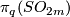 is correct, although the formula for
is correct, although the formula for 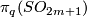 is incorrect because
is incorrect because 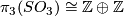 ).
Since
).
Since 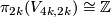 , we obtain that
, we obtain that 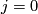 for
for 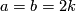 .
This and
.
This and 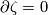 imply that
imply that 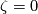 .
.

Lemma 6.6.
Let  be a
be a  -submanifold of
-submanifold of 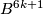 and let
and let 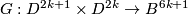 be an embedding such that
be an embedding such that 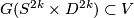 .
Then there is a smooth submanifold
.
Then there is a smooth submanifold 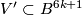 homeomorphic to
homeomorphic to 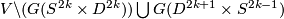 and such that
and such that 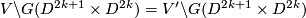 .
.
Lemma 6.6 is essentialy proved in [Haefliger1962,  3.3].
3.3].
Proof of Lemma 6.2 using Lemmas 6.4, 6.5.
By the fourth paragraph of the proof of Theorem 3.1 in [Haefliger1962], there is a basis 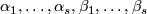 in
in 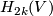 such that
such that 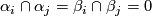 ,
, 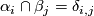 and
and 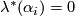 for any
for any 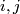 .
From Lemma 6.4 it follows that there are embeddings
.
From Lemma 6.4 it follows that there are embeddings 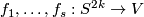 with pairwise disjoint images representing
with pairwise disjoint images representing 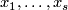 , respectively.
[!!!such that
, respectively.
[!!!such that ![f_{i*}[S^{2k}]=\alpha_i](/images/math/3/b/2/3b268affe6aabac0a3606326baf06b92.png) for every
for every 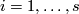 ]
]
For 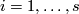 denote by
denote by 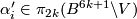 the homotopy class of the shift of
the homotopy class of the shift of 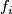 by the first vector of the framing of
by the first vector of the framing of  on
on 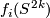 .
Since
.
Since 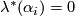 , we have
, we have 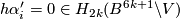 .
Since
.
Since 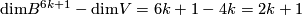 , the complement
, the complement 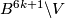 is
is 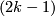 -connected.
Hence by Hurewicz Theorem
-connected.
Hence by Hurewicz Theorem 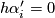 implies
implies 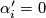 .
Therefore there are extensions
.
Therefore there are extensions 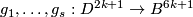 of
of 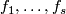 such that
such that 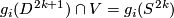 .
.
Take  such that
such that 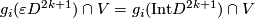 for any
for any 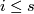 .
Take a tubular neighborhoods
.
Take a tubular neighborhoods 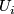 of
of 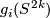 such that
such that 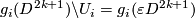 for any
for any 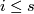 .
The algebraic intersection number of
.
The algebraic intersection number of 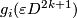 and
and 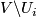 equals
equals ![\lambda^*(\alpha_i)=\lambda^*(g_{i*}[S^{2k}])=0](/images/math/7/4/2/7421b0739b5cce6ae14a3247ea7ab1fc.png) .
We have
.
We have 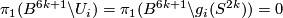 .
So we can apply item 2 of Lemma 6.3 to
.
So we can apply item 2 of Lemma 6.3 to 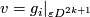 ,
, 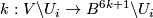 the inclusion, and
the inclusion, and 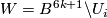 .
So we may assume that
.
So we may assume that 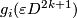 does not intersect
does not intersect 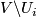 .
Hence we may assume that
.
Hence we may assume that 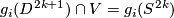 .
.
Apply Lemma 6.5 to 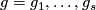 one by one, and to the manifold
one by one, and to the manifold  .
Denote by
.
Denote by 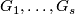 the resulting maps.
Define manifolds
the resulting maps.
Define manifolds 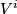 for
for 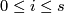 inductively.
Let
inductively.
Let 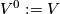 , and let
, and let 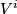 be a manifold
be a manifold 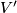 obtained applying Lemma 6.6 for
obtained applying Lemma 6.6 for 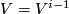 and
and 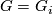 .
By Lemma 6.6,
.
By Lemma 6.6, 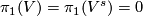 and
and 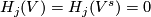 for
for 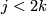 .
Since
.
Since 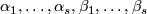 is a symplectic basis in
is a symplectic basis in 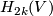 , it follows that
, it follows that 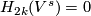 .
Then from Generalized Poincare conjecture proved by Smale it follows that
.
Then from Generalized Poincare conjecture proved by Smale it follows that 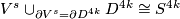 .
Hence
.
Hence 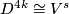 .
Then take
.
Then take 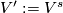 .
.

References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
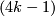 -spheres in
-spheres in 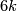 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Kervaire1965] M. A. Kervaire, Les noeuds de dimensions sup'erieures, Bull. Soc. Math. France 93 (1965), 225-271.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Pontryagin1959] L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, Amer. Math. Soc. Translations, Ser. 2, Vol. 11, Providence, R.I. (1959), 1–114. MR0115178 (22 #5980) Zbl 0084.19002
- [Prasolov2007] V. V. Prasolov, Elements of homology theory, American Mathematical Society, 2007. MR2313004 (2008d:55001) Zbl 1120.55001
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021
 3].
3].
2 Examples
There are smooth embeddings 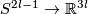 which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
which are not smoothly isotopic to the standard embedding. They are PS (piecewise smoothly) isotopic to the standard embedding (by the Zeeman Unknotting Spheres Theorem 2.3 of [Skopenkov2016c] and [Skopenkov2016f, Remark 1.1]).
Example 2.1. (a) Analogously to the Haefliger trefoil knot for any  one constructs a smooth embedding
one constructs a smooth embedding 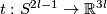 , see [Skopenkov2016h,
, see [Skopenkov2016h,  5].
For
5].
For  even
even  is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding;  represents a generator of
represents a generator of 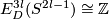 [Haefliger1962].
[Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 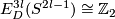 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 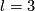 .
.
(b) For any 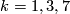 let
let 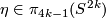 be the homotopy class of the Hopf map.
Denote by
be the homotopy class of the Hopf map.
Denote by 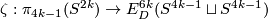 the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum
the Zeeman map, see [Skopenkov2016h, Definition 2.2].
The embedded connected sum 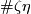 of the components of (a representative of)
of the components of (a representative of)  is not smoothly isotopic to the standard embedding;
is not smoothly isotopic to the standard embedding; 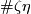 is a generator of
is a generator of 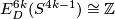 [Skopenkov2015a, Corollary 2.13].
[Skopenkov2015a, Corollary 2.13].
3 Invariants
Let us define the Haefliger invariant 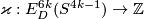 .
The definition is motivated by Haefliger's proof that any embedding
.
The definition is motivated by Haefliger's proof that any embedding 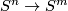 is isotopic to the standard embedding for
is isotopic to the standard embedding for 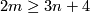 , and by analyzing what obstructs carrying this proof for
, and by analyzing what obstructs carrying this proof for 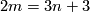 .
.
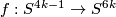 has a framing extendable to a framed embedding
has a framing extendable to a framed embedding 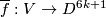 of a
of a  -manifold
-manifold  whose boundary is
whose boundary is 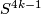 , and whose signature is zero. For an integer
, and whose signature is zero. For an integer 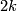 -cycle
-cycle  in
in  let
let 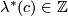 be the linking number of
be the linking number of 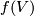 with a slight shift of
with a slight shift of 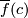 along the first vector of the framing. This defines a map
along the first vector of the framing. This defines a map 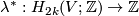 . This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique
. This map is a homomorphism (as opposed to the Arf map defined in a similar way [Pontryagin1959]). Then by Lefschetz duality there is a unique 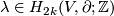 such that
such that ![\lambda^*[c]=\lambda\cap_V[c]](/images/math/b/2/8/b2878e69f979f9a0ca580faf4d104941.png) for any
for any ![[c]\in H_{2k}(V;\Z)](/images/math/8/9/f/89f1bbfc9e8e5259c8e842991bb8018b.png) . Since
. Since  has a normal framing, its intersection form
has a normal framing, its intersection form 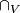 is even. (Indeed, represent a class in
is even. (Indeed, represent a class in 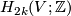 by a closed oriented
by a closed oriented  -submanifold
-submanifold  . Then
. Then ![\rho_2[c]\cap_V[c]=\overline{w_{2k}}(c\subset V)=\rho_2[c]\cap_VPDw_{2k}(V)=0](/images/math/7/8/8/788a4e3686035885f1e93cfe29a761c1.png) because
because  has a normal framing.) Hence
has a normal framing.) Hence 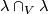 is an even integer. Define
is an even integer. Define 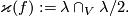
Since the signature of  is zero, there is a symplectic basis
is zero, there is a symplectic basis 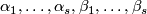 in
in 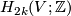 .
Then clearly
.
Then clearly
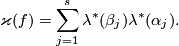
For an alternative definition via Seifert surfaces in 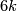 -space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,
-space, discovered in [Guillou&Marin1986], [Takase2004], see [Skopenkov2016t, the Kreck Invariant Lemma 4.5]. For a definition by Kreck, and for a generalization to 3-manifolds see [Skopenkov2016t,  4].
4].
Sketch of a proof that 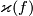 is well-defined (i.e. is independent of
is well-defined (i.e. is independent of  ,
, 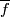 , and the framings), and is invariant under isotopy of
, and the framings), and is invariant under isotopy of  . [Haefliger1962, Theorem 2.6]
Analogously one defines
. [Haefliger1962, Theorem 2.6]
Analogously one defines 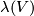 and
and 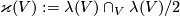 for a framed
for a framed  -submanifold
-submanifold  of
of 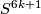 . Since
. Since 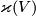 is a characteristic number, it is independent of framed cobordism. So
is a characteristic number, it is independent of framed cobordism. So 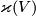 defines a homomorphism
defines a homomorphism 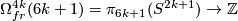 . The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
. The latter group is finite by the Serre theorem. Hence the homomorphism is trivial.
Since 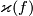 is a characteristic number, it is independent of framed cobordism of a framed
is a characteristic number, it is independent of framed cobordism of a framed  (and hence of the isotopy of a framed
(and hence of the isotopy of a framed  ).
).
Therefore 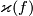 is a well-defined invariant of a framed cobordism class of a framed
is a well-defined invariant of a framed cobordism class of a framed  . By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3])
. By [Haefliger1962, 2.9] (cf. [Haefliger1962, 2.2 and 2.3]) 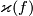 is also independent of the framing of
is also independent of the framing of  extendable to a framing of some
extendable to a framing of some  -manifold
-manifold  having trivial signature. QED
having trivial signature. QED
For definition of the attaching invariant 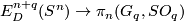 see [Haefliger1966], [Skopenkov2005,
see [Haefliger1966], [Skopenkov2005,  3].
3].
4 Classification
Theorem 4.1 [Levine1965, Corollary in p. 44], [Haefliger1966].
For 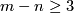 the group
the group  is finite unless
is finite unless 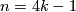 and
and 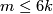 , when
, when  is the sum of
is the sum of  and a finite group.
and a finite group.
Theorem 4.2 (Haefliger-Milgram).
We have the following table for the group  ; in the whole table
; in the whole table 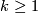 ; in the fifth column
; in the fifth column 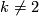 ; in the last two columns
; in the last two columns 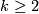 :
:
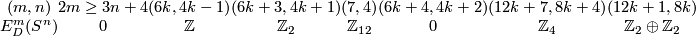
Proof for the first four columns, and for the fifth column when  is odd, are presented in [Haefliger1966, 8.15] (see also
is odd, are presented in [Haefliger1966, 8.15] (see also  6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,
6; some proofs are deduced from that paper using simple calculations, cf. [Skopenkov2005,  3]; there is a typo in [Haefliger1966, 8.15]:
3]; there is a typo in [Haefliger1966, 8.15]: 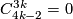 should be
should be 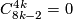 ). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases
). The remaining results follow from [Haefliger1966, 8.15] and [Milgram1972, Theorem F]. Alternative proofs for the cases 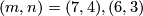 are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
are given in [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
Theorem 4.3 [Milgram1972, Corollary G].
We have 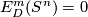 if and only if either
if and only if either 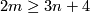 , or
, or 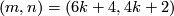 ,
or
,
or 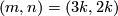 and
and 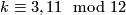 ,
or
,
or 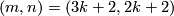 and
and 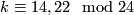 .
.
For a description of 2-components of  see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
see [Milgram1972, Theorem F]. Observe that no reliable reference (containing complete proofs) of results announced in [Milgram1972] appeared. Thus, strictly speaking, the corresponding results are conjectures.
The lowest-dimensional unknown groups  are
are 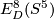 and
and 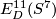 .
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
.
Hopefully application of Kreck surgery could be useful to find these groups, cf. [Skopenkov2005], [Crowley&Skopenkov2008], [Skopenkov2008].
For  the group
the group  has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
has been described as follows, in terms of exact sequences [Haefliger1966], cf. [Levine1965], [Haefliger1966a], [Milgram1972], [Habegger1986].
Theorem 4.4 [Haefliger1966].
For 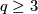 there is the following exact sequence of abelian groups:
there is the following exact sequence of abelian groups:
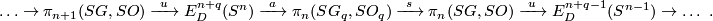
Here 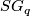 is the space of maps
is the space of maps 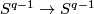 of degree
of degree  . Restricting a map from
. Restricting a map from 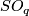 to
to 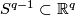 identifies
identifies 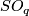 as a subspace of
as a subspace of 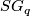 . Define
. Define 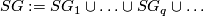 . Analogously define
. Analogously define  . Let
. Let  be the stabilization homomorphism. The attaching invariant
be the stabilization homomorphism. The attaching invariant  and the map
and the map  are defined in [Haefliger1966], see also [Skopenkov2005,
are defined in [Haefliger1966], see also [Skopenkov2005,  3].
3].
5 Some remarks on codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in  ), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.2 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots.
See e.g. the interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
6 Proof of classification of (4k-1)-knots in 6k-space
Theorem 6.1.
The Haefliger invariant 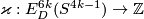 is injective for
is injective for  .
.
The proof is a certain simplification of [Haefliger1962]. We present an exposition structured to make it more accessible to non-specialists.
Lemma 6.2.
Let  be a framed
be a framed 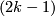 -connected
-connected  -submanifold of
-submanifold of 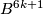 such that
such that 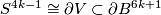 , signature of
, signature of  is zero, and
is zero, and 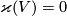 .
Then there is a submanifold
.
Then there is a submanifold 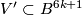 such that
such that 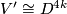 and
and  .
.
Proof of Theorem 6.1 using Lemma 6.2.
By the first three paragraphs of the proof of Theorem 3.1 in [Haefliger1962], for any embedding 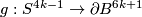 such that
such that 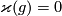 there is a framed
there is a framed 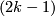 -connected
-connected  -submanifold
-submanifold  of
of 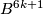 with zero signature such that
with zero signature such that 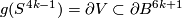 and
and 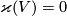 .
Then by Lemma 6.2 there is a submanifold
.
Then by Lemma 6.2 there is a submanifold 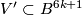 such that
such that 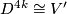 and
and 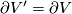 .
Recall that isotopy classes of embeddings
.
Recall that isotopy classes of embeddings 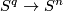 are in 1--1 correspondence with
are in 1--1 correspondence with  -cobordism classes of oriented submanifolds of
-cobordism classes of oriented submanifolds of  diffeomorphic to
diffeomorphic to 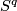 for
for 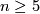 ,
, 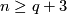 , cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence
, cf. [Haefliger1966, 1.8], [Kervaire1965].
Hence  is isotopic to standart embedding.
is isotopic to standart embedding. 
To prove Lemma 6.2 we need Lemmas 6.3, 6.4 and 6.5. Below manifolds can have non-empty boundaries.
Lemma 6.3 [Whitney lemma; [Prasolov2007],  22].
Let
22].
Let 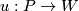 be a map from a connected oriented
be a map from a connected oriented  -manifold
-manifold  to a simply connected oriented
to a simply connected oriented 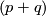 -manifold
-manifold  . If
. If 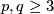 , then
, then
- If
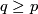 , there is a homotopy
, there is a homotopy 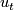 such that
such that 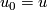 and
and 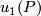 is an embedding.
is an embedding.
- Suppose in addition that
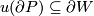 and there is a map
and there is a map 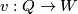 with
with 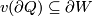 from a connected oriented
from a connected oriented  -manifold
-manifold 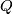 such that the algebraic intersection number of
such that the algebraic intersection number of 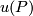 and
and 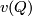 is zero. Then there is a homotopy
is zero. Then there is a homotopy 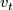 relative to the boundary such that
relative to the boundary such that 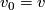 and
and 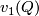 does not intersect
does not intersect 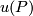 . If
. If  is an embedding, the homotopy
is an embedding, the homotopy 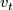 can be chosen so that
can be chosen so that 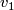 is an embedding.
is an embedding.
Below we denote by 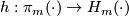 the Hurewicz map.
the Hurewicz map.
Lemma 6.4. Let  be a
be a 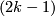 -connected
-connected  -manifold, and let
-manifold, and let 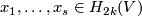 be homology classes such that
be homology classes such that 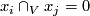 for every
for every 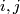 .
Then there are embeddings
.
Then there are embeddings 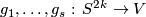 with pairwise disjoint images representing
with pairwise disjoint images representing 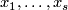 , respectively.
, respectively.
Proof. As  is
is 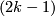 -connected,
-connected, 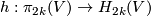 is an isomorphism.
For an element
is an isomorphism.
For an element 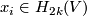 , let
, let 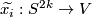 be a representative of the homotopy class
be a representative of the homotopy class 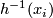 .
Applying item 1 of Lemma 6.3 to
.
Applying item 1 of Lemma 6.3 to  , we may assume that
, we may assume that 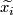 is an embedding.
is an embedding.
Make the following inductive procedure.
At the  -th step,
-th step, 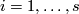 , assume that the embeddings
, assume that the embeddings 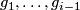 are already constructed, and we construct
are already constructed, and we construct 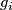 .
Since
.
Since 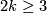 and
and  is simply connected,
is simply connected, 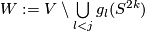 is simply connected for any
is simply connected for any 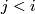 .
The algebraic intersection number of
.
The algebraic intersection number of 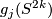 and
and 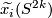 is zero for any
is zero for any  .
Hence we can apply item 2 of Lemma 6.3 to
.
Hence we can apply item 2 of Lemma 6.3 to 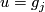 and
and 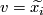 and
and  as above for any
as above for any 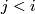 .
So
.
So 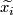 is replaced by a homotopic embedding
is replaced by a homotopic embedding 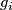 , and the images of
, and the images of 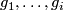 are pairwise disjoint.
After
are pairwise disjoint.
After  -th step we obtain a required set of embeddings.
-th step we obtain a required set of embeddings.

Lemma 6.5.
Let  be an orientable
be an orientable  -submanifold of
-submanifold of 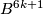 , and
, and 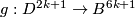 be an embedding such that
be an embedding such that 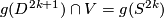 and over
and over  the manifold
the manifold  has a framing whose first vector is tangent to
has a framing whose first vector is tangent to 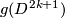 .
Assume that
.
Assume that  has zero algebraic self-intersection in
has zero algebraic self-intersection in  .
Then
.
Then  extends to an embedding
extends to an embedding 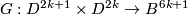 such that
such that 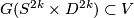 .
.
Proof. (A slightly different proof is presented in the proof of Proposition 3.3 in [Haefliger1962].)
Since  has zero algebraic self-intersection in
has zero algebraic self-intersection in  , the Euler class of the normal bundle of
, the Euler class of the normal bundle of  in
in  is zero.
Since over
is zero.
Since over  the manifold
the manifold  has a framing, we obtain that
has a framing, we obtain that  has a framing in
has a framing in  .
.
Identify all the normal spaces of 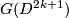 with the normal space at
with the normal space at 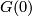 .
The normal framing
.
The normal framing  of
of  in
in  is orthogonal to
is orthogonal to 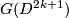 .
So
.
So  defines a map
defines a map 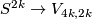 .
Let
.
Let 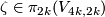 be the homotopy class of this map.
This is the obstruction to extending
be the homotopy class of this map.
This is the obstruction to extending  to a normal
to a normal 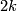 -framing of
-framing of  in
in 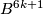 (so apriori
(so apriori 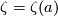 ).
It suffices to prove that
).
It suffices to prove that 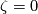 .
.
Consider the exact sequence of the bundle  :
:
 .
By the following well-known assertion,
.
By the following well-known assertion, 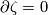 :
if
:
if 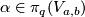 , then
, then 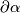 is the obstruction to trivialization of the orthogonal complement to the field of
is the obstruction to trivialization of the orthogonal complement to the field of  -frames in
-frames in 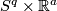 corresponding to a representative of
corresponding to a representative of  .
.
Consider a map of the exact sequences associated to the inclusion 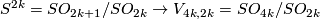 .
The composition
.
The composition 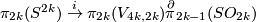 is the boundary map
is the boundary map 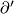 .
The group
.
The group 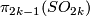 is in natural 1--1 correspondence with
is in natural 1--1 correspondence with 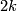 -bundles over
-bundles over 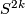 .
The image
.
The image 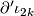 is the tangent bundle
is the tangent bundle  of
of 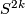 .
Since the Euler class of
.
Since the Euler class of 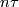 is
is 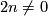 , the map
, the map 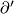 is injective.
is injective.
Alternatively, by [Fomenko&Fuchs2016, Corollary in  25.4]
25.4] 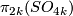 is a finite group (in [Fomenko&Fuchs2016, Corollary in
is a finite group (in [Fomenko&Fuchs2016, Corollary in  25.4] the formula for
25.4] the formula for 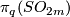 is correct, although the formula for
is correct, although the formula for 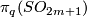 is incorrect because
is incorrect because 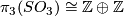 ).
Since
).
Since 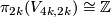 , we obtain that
, we obtain that 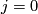 for
for 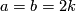 .
This and
.
This and 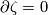 imply that
imply that 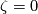 .
.

Lemma 6.6.
Let  be a
be a  -submanifold of
-submanifold of 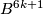 and let
and let 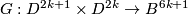 be an embedding such that
be an embedding such that 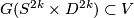 .
Then there is a smooth submanifold
.
Then there is a smooth submanifold 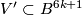 homeomorphic to
homeomorphic to 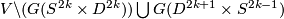 and such that
and such that 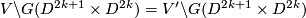 .
.
Lemma 6.6 is essentialy proved in [Haefliger1962,  3.3].
3.3].
Proof of Lemma 6.2 using Lemmas 6.4, 6.5.
By the fourth paragraph of the proof of Theorem 3.1 in [Haefliger1962], there is a basis 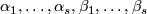 in
in 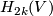 such that
such that 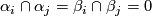 ,
, 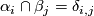 and
and 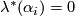 for any
for any 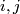 .
From Lemma 6.4 it follows that there are embeddings
.
From Lemma 6.4 it follows that there are embeddings 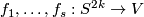 with pairwise disjoint images representing
with pairwise disjoint images representing 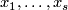 , respectively.
[!!!such that
, respectively.
[!!!such that ![f_{i*}[S^{2k}]=\alpha_i](/images/math/3/b/2/3b268affe6aabac0a3606326baf06b92.png) for every
for every  ]
]
For  denote by
denote by 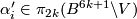 the homotopy class of the shift of
the homotopy class of the shift of  by the first vector of the framing of
by the first vector of the framing of  on
on 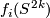 .
Since
.
Since 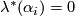 , we have
, we have 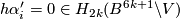 .
Since
.
Since 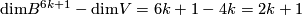 , the complement
, the complement 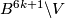 is
is 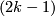 -connected.
Hence by Hurewicz Theorem
-connected.
Hence by Hurewicz Theorem 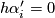 implies
implies 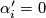 .
Therefore there are extensions
.
Therefore there are extensions 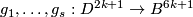 of
of 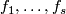 such that
such that 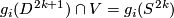 .
.
Take  such that
such that 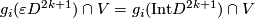 for any
for any 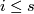 .
Take a tubular neighborhoods
.
Take a tubular neighborhoods 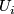 of
of 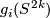 such that
such that 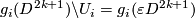 for any
for any  .
The algebraic intersection number of
.
The algebraic intersection number of  and
and 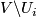 equals
equals ![\lambda^*(\alpha_i)=\lambda^*(g_{i*}[S^{2k}])=0](/images/math/7/4/2/7421b0739b5cce6ae14a3247ea7ab1fc.png) .
We have
.
We have 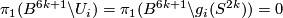 .
So we can apply item 2 of Lemma 6.3 to
.
So we can apply item 2 of Lemma 6.3 to 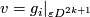 ,
, 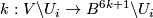 the inclusion, and
the inclusion, and 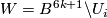 .
So we may assume that
.
So we may assume that 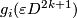 does not intersect
does not intersect 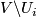 .
Hence we may assume that
.
Hence we may assume that 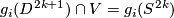 .
.
Apply Lemma 6.5 to 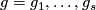 one by one, and to the manifold
one by one, and to the manifold  .
Denote by
.
Denote by 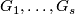 the resulting maps.
Define manifolds
the resulting maps.
Define manifolds 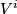 for
for 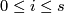 inductively.
Let
inductively.
Let 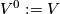 , and let
, and let 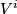 be a manifold
be a manifold 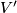 obtained applying Lemma 6.6 for
obtained applying Lemma 6.6 for 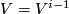 and
and 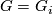 .
By Lemma 6.6,
.
By Lemma 6.6, 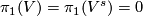 and
and 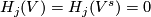 for
for 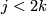 .
Since
.
Since 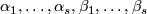 is a symplectic basis in
is a symplectic basis in 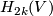 , it follows that
, it follows that 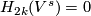 .
Then from Generalized Poincare conjecture proved by Smale it follows that
.
Then from Generalized Poincare conjecture proved by Smale it follows that 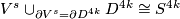 .
Hence
.
Hence 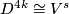 .
Then take
.
Then take 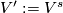 .
.

References
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Guillou&Marin1986] L. Guillou and A.Marin, Eds., A la r\'echerche de la topologie perdue, 1986, Progress in Math., 62, Birkhauser, Basel
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
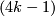 -spheres in
-spheres in 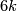 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Kervaire1965] M. A. Kervaire, Les noeuds de dimensions sup'erieures, Bull. Soc. Math. France 93 (1965), 225-271.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Pontryagin1959] L. S. Pontryagin, Smooth manifolds and their applications in homotopy theory, Amer. Math. Soc. Translations, Ser. 2, Vol. 11, Providence, R.I. (1959), 1–114. MR0115178 (22 #5980) Zbl 0084.19002
- [Prasolov2007] V. V. Prasolov, Elements of homology theory, American Mathematical Society, 2007. MR2313004 (2008d:55001) Zbl 1120.55001
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Takase2004] M. Takase, A geometric formula for Haefliger knots, Topology 43 (2004), no.6, 1425–1447. MR2081431 (2005e:57032) Zbl 1060.57021