Intersection form
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let  be a closed oriented
be a closed oriented  -manifold (PL or smooth). After Poincaré one studies the intersection number of transverse submanifolds or chains in
-manifold (PL or smooth). After Poincaré one studies the intersection number of transverse submanifolds or chains in  .
The intersection number gives a bilinear intersection product
.
The intersection number gives a bilinear intersection product
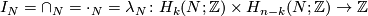
defined on the homology of  .
For
.
For 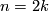 this is the intersection form of
this is the intersection form of  denoted by
denoted by 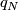 .
For
.
For 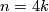 the signature of this form is the signature
the signature of this form is the signature 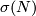 of
of  .
The intersection product is closely related to the notions of characteristic classes and linking form.
These are important invariants used in the classification of manifolds.
.
The intersection product is closely related to the notions of characteristic classes and linking form.
These are important invariants used in the classification of manifolds.
2 Definition
Take a triangulation  of
of  .
Denote by
.
Denote by 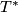 the dual cell subdivision.
Represent classes
the dual cell subdivision.
Represent classes ![[x]\in H_k(N;\Zz_2)](/images/math/7/0/7/707dad1546f3e2d2b347d942a382cab6.png) and
and ![[y]\in H_{n-k}(N;\Zz_2)](/images/math/4/6/7/4679c012b7ce2e40274b6c40ad1762d2.png) by cycles
by cycles  and
and  viewed as unions of
viewed as unions of  -simplices of
-simplices of  and
and 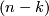 -simplices of
-simplices of 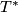 , respectively.
Define the modulo 2 intersection number by the formula
, respectively.
Define the modulo 2 intersection number by the formula
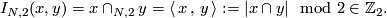
Define the modulo 2 intersection product
![\displaystyle I_{N,2}=\cap_{N,2}: H_k(N;\Zz_2) \times H_{n-k}(N;\Zz_2) \to \Zz_2\quad\text{by}\quad I_{N,2}([x],[y]):=I_{N,2}(x,y).](/images/math/3/a/9/3a9d69a54208e265e76fa92de305c3ef.png)
This product is well-defined because the intersection of a cycle and a boundary consists of an even number of points (by definition of a cycle and a boundary).
Analogously, counting intersections with signs, one defines the intersection number
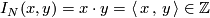
of integer chains 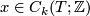 and
and 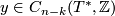 .
Clearly, the product of a cycle and a boundary is zero.
Hence this defines the above intersection product
.
Clearly, the product of a cycle and a boundary is zero.
Hence this defines the above intersection product
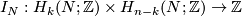 .
.
See [Kirby1989, Chapter II], [Skopenkov2005, Remark 2.3], [Skopenkov2015b,  6].
6].
Remark 2.1. (a) Using the notion of transversality, one can give an equivalent (and `more general') definition as follows. Take a  -chain
-chain 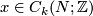 and an
and an 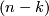 -chain
-chain 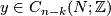 which are transverse to each other. The signed count of the intersections between
which are transverse to each other. The signed count of the intersections between  and
and  gives the intersection number
gives the intersection number 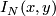 . A particular case is intersection number of immersions.
Then define the intersection product
. A particular case is intersection number of immersions.
Then define the intersection product 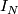 by
by ![I_N([x],[y]):=I_N(x,y)](/images/math/2/7/d/27d0a1c2e4c3335add9a5d5191f022ab.png) .
.
(b) Using the notion of cup product, one can give a dual (and so an equivalent) definition:
![\displaystyle I_N(x,y) = \langle x^*\smile y^*,[N]\rangle \in \Z,](/images/math/b/0/9/b098fae44db83b9fa8ee187a581e1526.png)
where 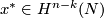 ,
, 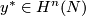 are the Poincaré duals of
are the Poincaré duals of  ,
,  , and
, and ![[N]](/images/math/3/5/8/3581986b0e7b591acd8d60e6ee096f5d.png) is the fundamental class of the manifold
is the fundamental class of the manifold  . We can also define the cup (cohomology intersection) product
. We can also define the cup (cohomology intersection) product
![\displaystyle I_N^*: H^k(N;\Zz) \times H^{n-k}(N;\Zz) \to \Zz \quad\text{by}\quad I_N^*(p,q) = \langle p \smile q , [N] \rangle .](/images/math/d/d/3/dd301a192d5a20a4267f2bf7881bcfb7.png)
The definition of a cup product is `dual' (and so is analogous) to the above definition of the intersection product on homology, but is more abstract. However, the definition of a cup product generalizes to complexes (and so to topological manifolds). This is an advantage for mathematicians who are interested in complexes and topological manifolds (not only in PL and smooth manifolds).
3 Simple properties
The following properties are easy to check using the simple direct definition; they also follow from simple properties of the cup product.
The intersection product is bilinear. Hence it vanishes on torsion elements. Thus it descends to a bilinear (integer) intersection pairing
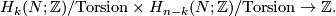
on the free modules.
We have
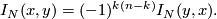
Hence for 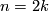
- If
 is even the form
is even the form 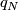 is symmetric:
is symmetric: 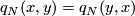 .
.
- If
 is odd the form
is odd the form 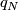 is skew-symmetric:
is skew-symmetric: 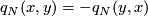 .
.
4 Poincaré duality
Theorem 4.1.[Poincaré duality] (a) The modulo 2 intersection product is non-degenerate.
(b) The integer intersection pairing is unimodular (in particular non-degenerate)
5 Definition of signature
Let  be a symmetric bilinear form on a free
be a symmetric bilinear form on a free 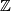 -module.
Denote by
-module.
Denote by 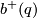 (
(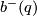 ) the number of positive (negative) eigenvalues.
) the number of positive (negative) eigenvalues.
Note that since  is symmetric, it is diagonalisable over the real numbers, so
is symmetric, it is diagonalisable over the real numbers, so 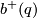 (
(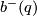 ) is the dimension of a maximal subspace on which the form is positive (negative) definite.
) is the dimension of a maximal subspace on which the form is positive (negative) definite.
Then the signature of  is defined to be
is defined to be
Tex syntax error
 is divisible by 4, the signature
is divisible by 4, the signature Tex syntax erroris defined to be the signature of the intersection form of
 .
.
6 Equivalence of bilinear forms
Let  and
and 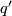 be unimodular bilinear forms on underlying free
be unimodular bilinear forms on underlying free 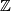 -modules
-modules  and
and 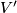 respectively. The forms
respectively. The forms  and
and 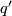 are called equivalent or isomorphic if there is an isomorphism
are called equivalent or isomorphic if there is an isomorphism 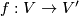 such that
such that 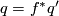 .
.
The rank of  is the rank of the underlying
is the rank of the underlying 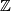 -module
-module  .
.
7 Skew-symmetric bilinear forms
The skew-symmetric hyperbolic form of rank  ,
, 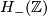 , is defined by the following intersection matrix
, is defined by the following intersection matrix
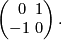
Proposition 7.1.
Every skey-symmetri uni-modular bilinear form over  ,
,  , isomorphic to the sum of some number of hyperbolic forms:
, isomorphic to the sum of some number of hyperbolic forms:
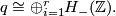
In particular the rank of  , in this case
, in this case 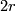 , is even.
, is even.
8 Symmetric bilinear forms
The classification of uni-modular definite symmetric bilinear forms is a deep and difficult problem. However the situation becomes much easier when the form is indefinite. Fundamental invariants are rank, signature and the following two.
A form  is called definite if it is positive or negative definite, otherwise it is called indefinite.
is called definite if it is positive or negative definite, otherwise it is called indefinite.
A form  may have two different types. It is of type even if
may have two different types. It is of type even if 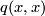 is an even number for any element
is an even number for any element  . Equivalently, if
. Equivalently, if  is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,
is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,  is said of type odd.
is said of type odd.
8.1 Classification of indefinite forms
There is a simple classification result of indefinite forms [Serre1970],[Milnor&Husemoller1973]:
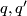 over
over 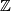 are equivalent if and only if
are equivalent if and only if  and
and 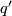 have the same rank, signature and type.
have the same rank, signature and type. There is a further invariant of a unimodular symmetric bilinear form  on
on  : An element
: An element 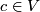 is called a characteristic vector of the form if one has
is called a characteristic vector of the form if one has
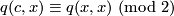
for all elements 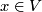 . Characteristic vectors always exist. In fact, when reduced modulo 2, the map
. Characteristic vectors always exist. In fact, when reduced modulo 2, the map 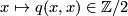 is linear. By unimodularity there therefore exists an element
is linear. By unimodularity there therefore exists an element  such that the map
such that the map 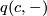 equals this linear map.
equals this linear map.
The form  is even if and only if
is even if and only if  is a characteristic vector.
If
is a characteristic vector.
If  and
and 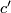 are characteristic vectors for
are characteristic vectors for  , then there is an element
, then there is an element  with
with 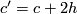 . This follows from unimodularity. As a consequence, the number
. This follows from unimodularity. As a consequence, the number 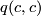 is independent of the chosen characteristic vector
is independent of the chosen characteristic vector  modulo 8. One can be more specific:
modulo 8. One can be more specific:
Proposition 8.2.
For a characteristic vector  of the unimodular symmetric bilinear form
of the unimodular symmetric bilinear form  one has
one has
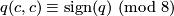
Proof:
Suppose  is a characteristic vector of
is a characteristic vector of  . Then
. Then 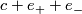 is a characteristic vector of the form
is a characteristic vector of the form
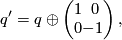
where 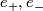 form basis elements of the additional
form basis elements of the additional  summand with square
summand with square 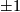 . We notice that
. We notice that
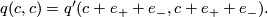
However, the form 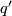 is indefinite, so the above classification theorem applies. In particular,
is indefinite, so the above classification theorem applies. In particular, 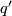 is odd and has the same signature as
is odd and has the same signature as  , so it is equivalent to the diagonal form with
, so it is equivalent to the diagonal form with 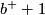 summands of (+1) and
summands of (+1) and 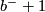 summands of
summands of 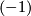 . This diagonal form has a characteristic vector
. This diagonal form has a characteristic vector 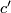 that is simply a sum of basis elements in which the form is diagonal. Of course
that is simply a sum of basis elements in which the form is diagonal. Of course 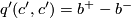 . The claim now follows from the fact that the square of a characteristic vector is independent of the chosen characteristic vector modulo 8.
. The claim now follows from the fact that the square of a characteristic vector is independent of the chosen characteristic vector modulo 8.
Corollary 8.3. The signature of an even (definite or indefinite) form is divisible by 8.
8.2 Examples, Realisations of indefinite forms
We shall show that any indefinite form permitted by the above theorem and corollary can be realised.
All possible values of rank and signature of odd forms are realised by direct sums of the forms of rank 1,
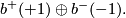
An even positive definite form of rank 8 is given by the  matrix
matrix
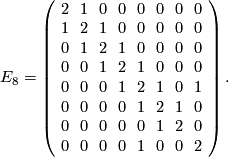
Likewise, the matrix 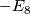 represents a negative definite even form of rank 8.
represents a negative definite even form of rank 8.
On the other hand, the matrix  given by
given by
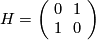
determines an indefinite even form of rank 2 and signature 0. It is easy to see that the direct sums
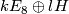
with 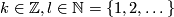 realise all unimodular symmetric indefinite even forms that are allowed by the above classification result. Here we use the convention that
realise all unimodular symmetric indefinite even forms that are allowed by the above classification result. Here we use the convention that 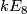 is the
is the  -fold direct sum of
-fold direct sum of 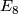 for positive
for positive  and
and 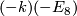 is the
is the 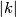 -fold direct sum of the negative definite form
-fold direct sum of the negative definite form 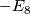 .
.
9 References
- [Kirby1989] R.C. Kirby, The topology of 4-manifolds, Lecture Notes in Math. 1374, Springer-Verlag, 1989. MR1001966 (90j:57012)
- [Milnor&Husemoller1973] J. Milnor and D. Husemoller, Symmetric bilinear forms, Springer-Verlag, New York, 1973. MR0506372 (58 #22129) Zbl 0292.10016
- [Serre1970] J. Serre, Cours d'arithmétique, Presses Universitaires de France, Paris, 1970. MR0255476 (41 #138) Zbl 0432.10001
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2015b] A. Skopenkov, Algebraic Topology From Geometric Viewpoint (in Russian), MCCME, Moscow, 2015, 2020. Preprint of a part in English
10 External links
- The Wikipedia page on Poincaré duality
 -manifold (PL or smooth). After Poincaré one studies the intersection number of transverse submanifolds or chains in
-manifold (PL or smooth). After Poincaré one studies the intersection number of transverse submanifolds or chains in  .
The intersection number gives a bilinear intersection product
.
The intersection number gives a bilinear intersection product
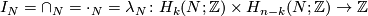
defined on the homology of  .
For
.
For 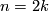 this is the intersection form of
this is the intersection form of  denoted by
denoted by 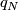 .
For
.
For 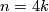 the signature of this form is the signature
the signature of this form is the signature 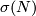 of
of  .
The intersection product is closely related to the notions of characteristic classes and linking form.
These are important invariants used in the classification of manifolds.
.
The intersection product is closely related to the notions of characteristic classes and linking form.
These are important invariants used in the classification of manifolds.
2 Definition
Take a triangulation  of
of  .
Denote by
.
Denote by 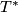 the dual cell subdivision.
Represent classes
the dual cell subdivision.
Represent classes ![[x]\in H_k(N;\Zz_2)](/images/math/7/0/7/707dad1546f3e2d2b347d942a382cab6.png) and
and ![[y]\in H_{n-k}(N;\Zz_2)](/images/math/4/6/7/4679c012b7ce2e40274b6c40ad1762d2.png) by cycles
by cycles  and
and  viewed as unions of
viewed as unions of  -simplices of
-simplices of  and
and 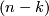 -simplices of
-simplices of 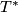 , respectively.
Define the modulo 2 intersection number by the formula
, respectively.
Define the modulo 2 intersection number by the formula
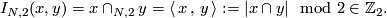
Define the modulo 2 intersection product
![\displaystyle I_{N,2}=\cap_{N,2}: H_k(N;\Zz_2) \times H_{n-k}(N;\Zz_2) \to \Zz_2\quad\text{by}\quad I_{N,2}([x],[y]):=I_{N,2}(x,y).](/images/math/3/a/9/3a9d69a54208e265e76fa92de305c3ef.png)
This product is well-defined because the intersection of a cycle and a boundary consists of an even number of points (by definition of a cycle and a boundary).
Analogously, counting intersections with signs, one defines the intersection number
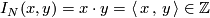
of integer chains 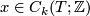 and
and 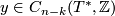 .
Clearly, the product of a cycle and a boundary is zero.
Hence this defines the above intersection product
.
Clearly, the product of a cycle and a boundary is zero.
Hence this defines the above intersection product
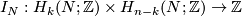 .
.
See [Kirby1989, Chapter II], [Skopenkov2005, Remark 2.3], [Skopenkov2015b,  6].
6].
Remark 2.1. (a) Using the notion of transversality, one can give an equivalent (and `more general') definition as follows. Take a  -chain
-chain 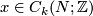 and an
and an 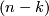 -chain
-chain 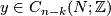 which are transverse to each other. The signed count of the intersections between
which are transverse to each other. The signed count of the intersections between  and
and  gives the intersection number
gives the intersection number 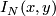 . A particular case is intersection number of immersions.
Then define the intersection product
. A particular case is intersection number of immersions.
Then define the intersection product 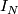 by
by ![I_N([x],[y]):=I_N(x,y)](/images/math/2/7/d/27d0a1c2e4c3335add9a5d5191f022ab.png) .
.
(b) Using the notion of cup product, one can give a dual (and so an equivalent) definition:
![\displaystyle I_N(x,y) = \langle x^*\smile y^*,[N]\rangle \in \Z,](/images/math/b/0/9/b098fae44db83b9fa8ee187a581e1526.png)
where 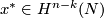 ,
, 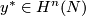 are the Poincaré duals of
are the Poincaré duals of  ,
,  , and
, and ![[N]](/images/math/3/5/8/3581986b0e7b591acd8d60e6ee096f5d.png) is the fundamental class of the manifold
is the fundamental class of the manifold  . We can also define the cup (cohomology intersection) product
. We can also define the cup (cohomology intersection) product
![\displaystyle I_N^*: H^k(N;\Zz) \times H^{n-k}(N;\Zz) \to \Zz \quad\text{by}\quad I_N^*(p,q) = \langle p \smile q , [N] \rangle .](/images/math/d/d/3/dd301a192d5a20a4267f2bf7881bcfb7.png)
The definition of a cup product is `dual' (and so is analogous) to the above definition of the intersection product on homology, but is more abstract. However, the definition of a cup product generalizes to complexes (and so to topological manifolds). This is an advantage for mathematicians who are interested in complexes and topological manifolds (not only in PL and smooth manifolds).
3 Simple properties
The following properties are easy to check using the simple direct definition; they also follow from simple properties of the cup product.
The intersection product is bilinear. Hence it vanishes on torsion elements. Thus it descends to a bilinear (integer) intersection pairing
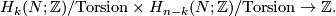
on the free modules.
We have
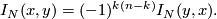
Hence for 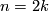
- If
 is even the form
is even the form 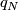 is symmetric:
is symmetric: 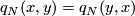 .
.
- If
 is odd the form
is odd the form 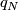 is skew-symmetric:
is skew-symmetric: 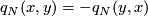 .
.
4 Poincaré duality
Theorem 4.1.[Poincaré duality] (a) The modulo 2 intersection product is non-degenerate.
(b) The integer intersection pairing is unimodular (in particular non-degenerate)
5 Definition of signature
Let  be a symmetric bilinear form on a free
be a symmetric bilinear form on a free 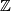 -module.
Denote by
-module.
Denote by 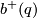 (
(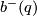 ) the number of positive (negative) eigenvalues.
) the number of positive (negative) eigenvalues.
Note that since  is symmetric, it is diagonalisable over the real numbers, so
is symmetric, it is diagonalisable over the real numbers, so 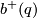 (
(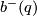 ) is the dimension of a maximal subspace on which the form is positive (negative) definite.
) is the dimension of a maximal subspace on which the form is positive (negative) definite.
Then the signature of  is defined to be
is defined to be
Tex syntax error
 is divisible by 4, the signature
is divisible by 4, the signature Tex syntax erroris defined to be the signature of the intersection form of
 .
.
6 Equivalence of bilinear forms
Let  and
and 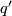 be unimodular bilinear forms on underlying free
be unimodular bilinear forms on underlying free 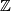 -modules
-modules  and
and 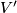 respectively. The forms
respectively. The forms  and
and 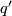 are called equivalent or isomorphic if there is an isomorphism
are called equivalent or isomorphic if there is an isomorphism 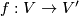 such that
such that 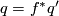 .
.
The rank of  is the rank of the underlying
is the rank of the underlying 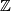 -module
-module  .
.
7 Skew-symmetric bilinear forms
The skew-symmetric hyperbolic form of rank  ,
, 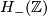 , is defined by the following intersection matrix
, is defined by the following intersection matrix
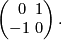
Proposition 7.1.
Every skey-symmetri uni-modular bilinear form over  ,
,  , isomorphic to the sum of some number of hyperbolic forms:
, isomorphic to the sum of some number of hyperbolic forms:
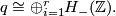
In particular the rank of  , in this case
, in this case 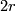 , is even.
, is even.
8 Symmetric bilinear forms
The classification of uni-modular definite symmetric bilinear forms is a deep and difficult problem. However the situation becomes much easier when the form is indefinite. Fundamental invariants are rank, signature and the following two.
A form  is called definite if it is positive or negative definite, otherwise it is called indefinite.
is called definite if it is positive or negative definite, otherwise it is called indefinite.
A form  may have two different types. It is of type even if
may have two different types. It is of type even if 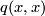 is an even number for any element
is an even number for any element  . Equivalently, if
. Equivalently, if  is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,
is written as a square matrix in a basis, it is even if the elements on the diagonal are all even. Otherwise,  is said of type odd.
is said of type odd.
8.1 Classification of indefinite forms
There is a simple classification result of indefinite forms [Serre1970],[Milnor&Husemoller1973]:
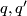 over
over 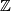 are equivalent if and only if
are equivalent if and only if  and
and 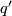 have the same rank, signature and type.
have the same rank, signature and type. There is a further invariant of a unimodular symmetric bilinear form  on
on  : An element
: An element 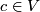 is called a characteristic vector of the form if one has
is called a characteristic vector of the form if one has
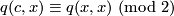
for all elements 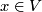 . Characteristic vectors always exist. In fact, when reduced modulo 2, the map
. Characteristic vectors always exist. In fact, when reduced modulo 2, the map 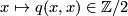 is linear. By unimodularity there therefore exists an element
is linear. By unimodularity there therefore exists an element  such that the map
such that the map 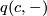 equals this linear map.
equals this linear map.
The form  is even if and only if
is even if and only if  is a characteristic vector.
If
is a characteristic vector.
If  and
and 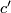 are characteristic vectors for
are characteristic vectors for  , then there is an element
, then there is an element  with
with 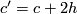 . This follows from unimodularity. As a consequence, the number
. This follows from unimodularity. As a consequence, the number 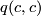 is independent of the chosen characteristic vector
is independent of the chosen characteristic vector  modulo 8. One can be more specific:
modulo 8. One can be more specific:
Proposition 8.2.
For a characteristic vector  of the unimodular symmetric bilinear form
of the unimodular symmetric bilinear form  one has
one has
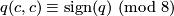
Proof:
Suppose  is a characteristic vector of
is a characteristic vector of  . Then
. Then 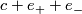 is a characteristic vector of the form
is a characteristic vector of the form
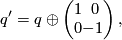
where 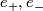 form basis elements of the additional
form basis elements of the additional 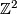 summand with square
summand with square 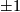 . We notice that
. We notice that
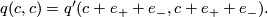
However, the form 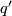 is indefinite, so the above classification theorem applies. In particular,
is indefinite, so the above classification theorem applies. In particular, 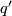 is odd and has the same signature as
is odd and has the same signature as  , so it is equivalent to the diagonal form with
, so it is equivalent to the diagonal form with 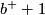 summands of (+1) and
summands of (+1) and 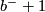 summands of
summands of 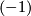 . This diagonal form has a characteristic vector
. This diagonal form has a characteristic vector 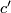 that is simply a sum of basis elements in which the form is diagonal. Of course
that is simply a sum of basis elements in which the form is diagonal. Of course 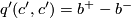 . The claim now follows from the fact that the square of a characteristic vector is independent of the chosen characteristic vector modulo 8.
. The claim now follows from the fact that the square of a characteristic vector is independent of the chosen characteristic vector modulo 8.
Corollary 8.3. The signature of an even (definite or indefinite) form is divisible by 8.
8.2 Examples, Realisations of indefinite forms
We shall show that any indefinite form permitted by the above theorem and corollary can be realised.
All possible values of rank and signature of odd forms are realised by direct sums of the forms of rank 1,
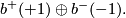
An even positive definite form of rank 8 is given by the 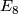 matrix
matrix
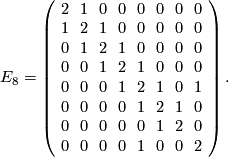
Likewise, the matrix 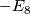 represents a negative definite even form of rank 8.
represents a negative definite even form of rank 8.
On the other hand, the matrix  given by
given by
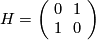
determines an indefinite even form of rank 2 and signature 0. It is easy to see that the direct sums
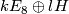
with 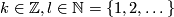 realise all unimodular symmetric indefinite even forms that are allowed by the above classification result. Here we use the convention that
realise all unimodular symmetric indefinite even forms that are allowed by the above classification result. Here we use the convention that 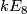 is the
is the  -fold direct sum of
-fold direct sum of 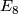 for positive
for positive  and
and 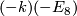 is the
is the 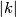 -fold direct sum of the negative definite form
-fold direct sum of the negative definite form 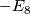 .
.
9 References
- [Kirby1989] R.C. Kirby, The topology of 4-manifolds, Lecture Notes in Math. 1374, Springer-Verlag, 1989. MR1001966 (90j:57012)
- [Milnor&Husemoller1973] J. Milnor and D. Husemoller, Symmetric bilinear forms, Springer-Verlag, New York, 1973. MR0506372 (58 #22129) Zbl 0292.10016
- [Serre1970] J. Serre, Cours d'arithmétique, Presses Universitaires de France, Paris, 1970. MR0255476 (41 #138) Zbl 0432.10001
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2015b] A. Skopenkov, Algebraic Topology From Geometric Viewpoint (in Russian), MCCME, Moscow, 2015, 2020. Preprint of a part in English
10 External links
- The Wikipedia page on Poincaré duality