Talk:Whitehead torsion (Ex)

We can compute that

$(1-t-t^{-1})\cdot(1-t^2-t^3) = 1$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}(1-t-t^{-1})\cdot(1-t^2-t^3) = 1$ 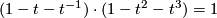so the element is a unit. The map 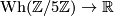$\mathrm{Wh}(\Z/5\Z) \to \Rr$$\mathrm{Wh}(\Z/5\Z) \to \Rr$ can be described as follows.

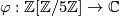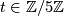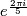There is a ring homomorphism $\varphi: \Zz\lbrack \Zz/5\Zz \rbrack \to \Cc$$\varphi: \Zz\lbrack \Zz/5\Zz \rbrack \to \Cc$ sending a generator $t \in \Zz/5\Zz$$t \in \Zz/5\Zz$ to $e^{\frac{2\pi i}{5}}$$e^{\frac{2\pi i}{5}}$ . Now we consider the composite

$\displaystyle \xymatrix{K_1(\Zz\lbrack \Zz/5\Zz \rbrack) \ar[r]^-{\varphi_*} \ar@{->>}[d] & K_1(\Cc) \ar[r]^-{\det} & \Cc^\times \ar[r]^-{|-|} & \Rr_{>0} \ar[r]^-{\ln} & \Rr \\ \mathrm{Wh}(\Zz/5\Zz) \ar@/_1.3pc/@{-->}[urrrr] & & & & }$

By definition it takes the class of some automorphism 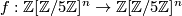$f: \Zz\lbrack \Zz/5\Zz \rbrack^n \to \Zz\lbrack \Zz/5\Zz \rbrack^n$$f: \Zz\lbrack \Zz/5\Zz \rbrack^n \to \Zz\lbrack \Zz/5\Zz \rbrack^n$ to the real number 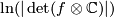$\ln(| \det(f\otimes \Cc) |)$$\ln(| \det(f\otimes \Cc) |)$ . The above composite is a well-defined group homomorphism as all single maps are well-defined group homomorphisms, so it remains to check whether it factors over the Whitehead group. So let 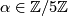$\alpha \in \Zz/5\Zz$$\alpha \in \Zz/5\Zz$. Then by left multiplication it defines a map ;

$\displaystyle \xymatrix{ \Zz\lbrack \Zz/5\Zz \rbrack \ar[r]^-{\alpha} & \Zz\lbrack \Zz/5\Zz \rbrack}$

and inducing it up to the complex numbers gives the map ;

$\displaystyle \xymatrix{\Cc \ar[r]^-{e^{\frac{2\pi i\alpha}{5}}} & \Cc}$

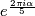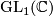given by multiplication by $e^{\frac{2\pi i\alpha}{5}}$$e^{\frac{2\pi i\alpha}{5}}$ . On $\mathrm{GL}_1(\Cc)$$\mathrm{GL}_1(\Cc)$ the determinant is of course the identity map, so we need to compute ;

$\displaystyle \ln(| e^{\frac{2\pi i\alpha}{5}} |) = 0$ $$\displaystyle \ln(| e^{\frac{2\pi i\alpha}{5}} |) = 0$$

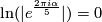
which follows since 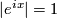$| e^{ix} | = 1$$| e^{ix} | = 1$ for all real numbers $x$$x$ , in particular for $\frac{2\pi \alpha}{5}$$\frac{2\pi \alpha}{5}$ .

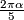Now to show that 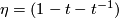$\eta = (1-t-t^{-1})$$\eta = (1-t-t^{-1})$ generates an infinite cyclic subgroup of 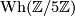$\mathrm{Wh}(\Zz/5\Zz)$$\mathrm{Wh}(\Zz/5\Zz)$ it suffices to show that 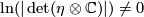$\ln(| \det(\eta\otimes \Cc)|) \neq 0$$\ln(| \det(\eta\otimes \Cc)|) \neq 0$ because then 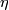$\eta$$\eta$ is not a torsion element.

For this we simply calculate that ;

$\displaystyle \eta\otimes \Cc = 1 - e^{\frac{2\pi}{5}} - e^{\frac{-2\pi}{5}}$ $$\displaystyle \eta\otimes \Cc = 1 - e^{\frac{2\pi}{5}} - e^{\frac{-2\pi}{5}}$$

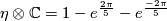
hence it follows that ;

$\displaystyle | \eta\otimes \Cc | = 1 - 2\cos(\frac{2\pi}{5}) \neq 1$ $$\displaystyle | \eta\otimes \Cc | = 1 - 2\cos(\frac{2\pi}{5}) \neq 1$$

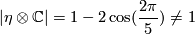
since 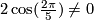$2\cos(\frac{2\pi}{5}) \neq 0$$2\cos(\frac{2\pi}{5}) \neq 0$ . In particular applying the logarithm we get ;

$\displaystyle \ln(|\det(\eta\otimes \Cc)|) \neq 0$ $$\displaystyle \ln(|\det(\eta\otimes \Cc)|) \neq 0$$

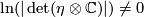
which we wanted to show.