Thom spaces (Ex)
From Manifold Atlas
(Redirected from Thom spaces)
Exercise 0.1.
Let 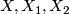 be
be  -complexes and let
-complexes and let 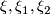 be vector bundles
over
be vector bundles
over  respectively.
Denote by
respectively.
Denote by 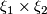 the product bundle over
the product bundle over 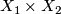 .
Find homeomorphisms
.
Find homeomorphisms
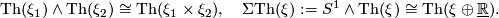
With the following exercises we work out the details of [Lück2001, page 58f].
Exercise 0.2.
Let 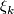 be the universal oriented vector bundle of rank
be the universal oriented vector bundle of rank 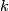 and let
and let 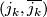 :
: 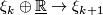 be a bundle map. Define
be a bundle map. Define
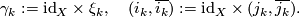
Show that for all 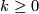 we have
we have 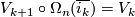 .
.
Exercise 0.3. Define
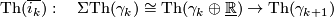
and
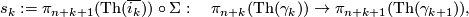
where 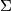 :
: 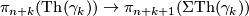 is the suspension homomorphism.
Show that for all
is the suspension homomorphism.
Show that for all 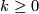 we have
we have 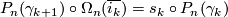 .
.
Question 0.4. Can we do similar things for unoriented manifolds, manifolds with spin structure,...?