Template:Arone&Krushkal2021
From Manifold Atlas
G. Arone, V. Krushkal, Embedding obstructions in 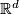 from the Goodwillie-Weiss calculus and Whitney disks, arxiv preprint.
from the Goodwillie-Weiss calculus and Whitney disks, arxiv preprint.
[edit] 1 Comment
- It is simple and known since [Wu1965] that if a space
 embeds into
embeds into 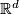 , then for any
, then for any  there exists a
there exists a 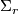 -equivariant map
-equivariant map 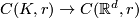 , see also survey [Skopenkov2006, end of
, see also survey [Skopenkov2006, end of  5]. It would be nice to know if (for any
5]. It would be nice to know if (for any  , not only for
, not only for 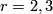 )
) 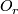 is the primary obstruction (in the sense of classical obstruction theory) to the existence of a
is the primary obstruction (in the sense of classical obstruction theory) to the existence of a 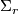 -equivariant map
-equivariant map 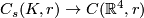 agreeing with the given
agreeing with the given 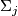 -equivariant maps
-equivariant maps 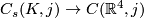 ,
, 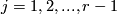 . Cf. Proposition 2.11. This would clarify the relation of Goodwillie-Weiss calculus (in this particular situation) to classical algebraic topology.
. Cf. Proposition 2.11. This would clarify the relation of Goodwillie-Weiss calculus (in this particular situation) to classical algebraic topology.
- It would be nice to mention that analogous (but simpler) obstruction to the existence of a map without
 -fold points (more precisely, of an almost
-fold points (more precisely, of an almost  -embedding) is known. See e.g. the survey [Skopenkov2016, end of
-embedding) is known. See e.g. the survey [Skopenkov2016, end of  1.3]. This analogy suggests that it would be nice to know if the Arone-Krushkal obstructions
1.3]. This analogy suggests that it would be nice to know if the Arone-Krushkal obstructions
- are trivial for  not a prime power (for the analogous result on obstruction to
not a prime power (for the analogous result on obstruction to  -almost embeddability see the survey [Skopenkov2016, Theorem 3.3 (\"Ozaydin)]);
-almost embeddability see the survey [Skopenkov2016, Theorem 3.3 (\"Ozaydin)]);
- have finite order for any  (for the analogous obstruction
(for the analogous obstruction 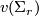 to
to  -almost embeddability we have
-almost embeddability we have 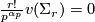 , see the survey [Skopenkov2016,
, see the survey [Skopenkov2016,  3.2]);
3.2]);
- are sufficient to almost-embeddability (for the analogous results on  -almost embeddability see the survey [Skopenkov2016, Theorems 3.1 (Mabillard-Wagner) and 3.5]).
-almost embeddability see the survey [Skopenkov2016, Theorems 3.1 (Mabillard-Wagner) and 3.5]).
- For the well-known geometric definition of the Milnor number
 see e.g. [Skopenkov2012,
see e.g. [Skopenkov2012,  4.6,
4.6,  4.7]. Definition 3.4 is analogous to the following equivalent definition, which is presumably due to Matsumoto (see paper, page 2, the second paragraph after theorem 1, citation of [37] for the triple linking number case, i.e., n=1). Assume that
4.7]. Definition 3.4 is analogous to the following equivalent definition, which is presumably due to Matsumoto (see paper, page 2, the second paragraph after theorem 1, citation of [37] for the triple linking number case, i.e., n=1). Assume that 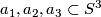 are pairwise disjoint oriented knots such that
are pairwise disjoint oriented knots such that 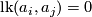 . Let
. Let 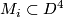 ,
, 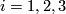 , be general position oriented singular disks spanned by the knots
, be general position oriented singular disks spanned by the knots 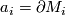 . Since
. Since 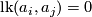 , we have
, we have 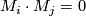 . So we can split the points from
. So we can split the points from 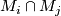 into pairs of points having opposite signs. Take disjoint union
into pairs of points having opposite signs. Take disjoint union 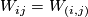 of the naturally oriented Whitney disks corresponding to this splitting. (The orientation of
of the naturally oriented Whitney disks corresponding to this splitting. (The orientation of 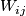 is induced from the orientation on their boundary circles which are oriented from the negative intersection point to the positive intersection point along
is induced from the orientation on their boundary circles which are oriented from the negative intersection point to the positive intersection point along 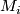 , and vice versa along
, and vice versa along 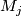 .) Then In this definition singular disks could not be replaced by Seifert surfaces because Borromean rings in
.) Then In this definition singular disks could not be replaced by Seifert surfaces because Borromean rings in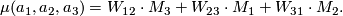
 bound pairwise disjoint Seifert surfaces in
bound pairwise disjoint Seifert surfaces in 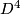 .
.
- The usual name for transformations analogous to `stabilization' of Definition 3.7 (resulting in adding a coboundary to a cocycle) is `(generalized) van Kampen finger move'. For such transformations see Figure 1 and surveys [Skopenkov2006,
 4,
4,  8], [Skopenkov2016, end of
8], [Skopenkov2016, end of  3.3], [Skopenkov2018i,
3.3], [Skopenkov2018i,  1.5.3].
1.5.3].
- In
 8.4, 2nd paragraph, instead of `PL embeddability is established' there should be `PL almost embeddability is established'.
8.4, 2nd paragraph, instead of `PL embeddability is established' there should be `PL almost embeddability is established'.
[edit] 2 References
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2012] A. Skopenkov, Algebraic Topology From Algorithmic Standpoint, draft of a book (partly in Russian)
- [Skopenkov2016] A. Skopenkov, A user's guide to the topological Tverberg Conjecture, Russian Math. Surveys, 73:2 (2018), 323--353. Full updated version: arXiv:1605.05141.
- [Skopenkov2018i] A. Skopenkov, Invariants of graph drawings in the plane, Arnold Math. J., 6 (2020) 21-55. Full updated version: arXiv:1805.10237
- [Wu1965] W. T. Wu, A Theory of Embedding, Immersion and Isotopy of Polytopes in an Euclidean Space, Peking: Science Press, 1965.