Talk:S-duality II (Ex)
The map we use is closely related to the previous exercise so we will copy and paste some terminology used there - note that we will use 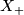 where
where  is used there, and have changed the diagonal map appropriately:
is used there, and have changed the diagonal map appropriately:
Let  be a finite CW complex. Embed
be a finite CW complex. Embed 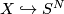 with regular neighbourhood
with regular neighbourhood  , so that
, so that
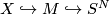
with 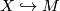 a homotopy-equivalence and
a homotopy-equivalence and  an
an  -dimensional manifold-with-boundary embedded in
-dimensional manifold-with-boundary embedded in 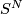 .
.
Now let
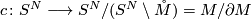
be the collapse map,
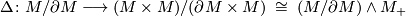
be the map induced by
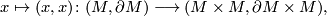
and let  be the composite
be the composite
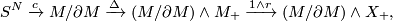
where 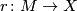 is a chosen homotopy-inverse for
is a chosen homotopy-inverse for  .
.
Solution 0.1.
First, take 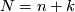 where
where  is the dimension of
is the dimension of  . Fix a Thom class
. Fix a Thom class 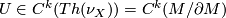 and a class
and a class ![[X]\in C_n(X)](/images/math/3/d/f/3df3efce268943425d48ff4572ec6271.png) determining the Poincaré duality for
determining the Poincaré duality for  .
.
Take reduced chain complexes (denoted 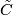 ) for the spaces in the composite
) for the spaces in the composite  . We then make a choice of Eilenberg-Zilber map (unique up to chain homotopy) so that
. We then make a choice of Eilenberg-Zilber map (unique up to chain homotopy) so that
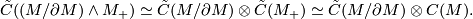
The chain-level slant map now involves a choice - in general if we have two chains  and
and  then the slant involves a choice of ordering to form
then the slant involves a choice of ordering to form 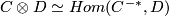 or
or 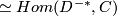 . When considering
. When considering  -duality, the choice represents the symmetry that
-duality, the choice represents the symmetry that 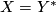 iff
iff 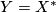 . We will need to choose the slant map so that
. We will need to choose the slant map so that
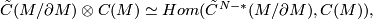
this is followed with the map induced by 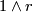 so that the overall slant map isomorphism induced is
so that the overall slant map isomorphism induced is ![-\backslash \alpha_*([S^N]):\tilde{H}^{N-*}(M/\partial M)\to H_*(X)](/images/math/8/e/1/8e1c7d51c0140af5ad6afd2aa800cb1d.png) (see the previous exercise for a justification of this, albeit for the opposite choice of slant).
(see the previous exercise for a justification of this, albeit for the opposite choice of slant).
Considering the composite  again, note that before we use the smash map
again, note that before we use the smash map 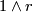 , it is still valid to use the identity for slant product that for any
, it is still valid to use the identity for slant product that for any 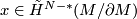 , we have
, we have
![\displaystyle x\setminus \Delta_*(c_*([S^N])) \;=\; x\cap c_*([S^N]) \;\in\; H_{*}(M),](/images/math/7/6/8/76833b88b266e902838050d6f30df794.png)
as this is still a (relative) definition of cap product on the chain level.
We now want to know how the slant map interacts with the smash map 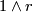 . In general for any
. In general for any 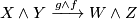 and
and 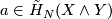 , we have a commutative diagram:
, we have a commutative diagram:
![\displaystyle \xymatrix{ C(X\wedge Y)\ar[d]_{(g\wedge f)_*}\ar[r]^-{\simeq}&Hom(C(X)^{-*},C(Y))\ar[d]\\ C(W\wedge Z)\ar[r]^-{\simeq}&Hom(C(W)^{-*},C(Z))}](/images/math/3/c/7/3c741779ad1db8b06b0e702d97b16f68.png)
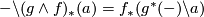 .
.
Hence
![\displaystyle r_*(U\backslash \Delta(c_*([S^N])))=r_*(U\cap c_*([S^N])).](/images/math/3/b/8/3b80ffe83f67a907ac23c228a19cf82b.png)
![\pm[X]](/images/math/c/7/7/c77a7fefb3add7f3afeeb7e707890a3e.png) by the definition of the Spivak normal structure.
by the definition of the Spivak normal structure.
Solution 0.2.
This now follows easily from breaking the diagram down in a careful fashion to
![\displaystyle \xymatrix{ C^{n-*}(X)\ar[ddr]^{-\cap [X]}\ar[r]^{r^*}& C^{n-*}(M)\ar[r]^-{-\cup U} &C^{n+k-*}(M,\partial M)\ar[ddl]^{-\backslash \alpha_*([S^N])}\\ &&\\ &C(X)&}](/images/math/7/b/2/7b27f595d498f2d9d12fa22fa3a8c418.png)
and noting that following the top side of the diagram round to 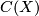 gives
gives
![\displaystyle r_*((r^*(-)\cup U)\cap c_*([S^N]))=-\cap r_*(U\cap c_*([S^N]))](/images/math/3/5/e/35e54d712351c60c07fdd81b2be6c0b4.png)