Oberwolfach Surgery Seminar 2012: Discussion
This page is for discussion following the seminar
- General information
- Exercises
- Glossary
- Surgery on the Manifold Atlas
- Videos of the Oberwolfach lectures
- Philipp Kühl's stenographic lecture notes.
[edit] 1 Recommended reading
Tibor's comments on 07/06/2012:
For a quick and very readable basic introduction to algebraic surgery I would very much recommend Andrew's article:
- Foundations of algebraic surgery, Topology of high-dimensional manifolds, No. 1, 2 (Trieste, 2001), Abdus Salam Int. Cent. Theoret. Phys., Trieste (2002), 491–514. [Ranicki2002a]
Here the basic idea of algebraic surgery is explained and the relation to cobordisms.
For a quick introduction to the algebraic surgery exact sequence which involves the structure group 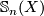 I would recommend Andrew's article
I would recommend Andrew's article
- The structure set of an arbitrary space, the algebraic surgery exact sequence and the total surgery obstruction, School on High-dimensional Manifold Topology, 519--538, ICTP Trieste (2002). [Ranicki2002b]
A general note about the notation. There are two notations for the groups that measure the difference between the quadratic and symmetric  -groups. One is
-groups. One is 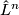 and the other
and the other 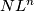 . These groups have different definitions, hence the notation, but they are isomorphic, see Proposition 2.11 in [Ranicki1992].
. These groups have different definitions, hence the notation, but they are isomorphic, see Proposition 2.11 in [Ranicki1992].
Andrew recommended the lecture notes of Adam Mole from Andrew's 2008 Muenster course, which I can only agree with. Here you often find more motivation than in published articles.
Of those published articles, I would recommend to begin with the first two for the basics of algebraic surgery (but now this is on a higher level than those above):
- The algebraic theory of surgery I., Proc. London Math. Soc. (3) 40, 87--192 (1980) [Ranicki1980]
- The algebraic theory of surgery II., Proc. London Math. Soc. (3) 40, 193--283 (1980) [Ranicki1980a]
For the algebraic surgery exact sequence and the total surgery obstruction, of course there is the blue book
- Algebraic L-theory and Topological Manifolds, Cambridge Tracts in Mathematics 102, CUP (1992) [Ranicki1992]
which can be accompanied by
- The total surgery obstruction revisited by P.Kuehl, T.Macko and A.Mole arXiv:1104.50 (2011) [Kühl&Macko&Mole2011]
which is meant partly as a readable summary (mostly without proofs) of the setup of the algebraic surgery exact sequence and partly as a place where some more details in the technical parts of the proof that TSO is TSO are given.
Of course there is the original paper of Andrew:
- The total surgery obstruction, Algebraic topology, Aarhus 1978 (Proc. Sympos., Univ. Aarhus, Aarhus, 1978), Springer (1979), 275–316 [Ranicki1979]
with most of the great ideas already present (although in a slightly different form sometimes, it's 35 years old, after all).
Finally, from a more modern point of view (using the language of  -categories), there are lecture notes of Jacob Lurie:
-categories), there are lecture notes of Jacob Lurie:
- Algebraic L-theory and surgery, Jacob Lurie's 2011 Harvard course.
Links to all the material above can be found on Andrew's website. Some of it is under the links "Surgery bits and pieces" -> "Books, papers, theses, notes, links, etc": in particular Adam Mole's notes and Jacob Lurie's lecture notes may be found here. The easiest way to find items on Andrew's website is to just Google for their titles!
[edit] 2 References
- [Kühl&Macko&Mole2011] P. Kuehl, T. Macko and A. Mole, The total surgery obstruction revisited, (2011). Available at the arXiv:1104.5092.
- [Ranicki1979] A. Ranicki, The total surgery obstruction, Algebraic topology, Aarhus 1978 (Proc. Sympos., Univ. Aarhus, Aarhus, 1978), Springer (1979), 275–316. MR561227 (81e:57034) Zbl 1069.57019
- [Ranicki1980] A. Ranicki, The algebraic theory of surgery. I. Foundations, Proc. London Math. Soc. (3) 40 (1980), no.1, 87–192. MR560997 (82f:57024a) Zbl 0471.57012
- [Ranicki1980a] A. Ranicki, The algebraic theory of surgery. II. Applications to topology, Proc. London Math. Soc. (3) 40 (1980), no.2, 193–283. MR566491 (82f:57024b) Zbl 0471.57012
- [Ranicki1992] A. A. Ranicki, Algebraic
 -theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
-theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
- [Ranicki2002a] A. Ranicki, Foundations of algebraic surgery, Topology of high-dimensional manifolds, No. 1, 2 (Trieste, 2001), Abdus Salam Int. Cent. Theoret. Phys., Trieste (2002), 491–514. MR1937022 (2004a:57042) Zbl 0471.57010
- [Ranicki2002b] A. Ranicki, The structure set of an arbitrary space, the algebraic surgery exact sequence and the total surgery obstruction, Topology of high-dimensional manifolds, No. 1, 2 (Trieste, 2001), Abdus Salam Int. Cent. Theoret. Phys., Trieste (2002), 515–538. MR1937023 (2004a:57043) Zbl 1069.57019