Classifying Poincaré complexes via fundamental triples
|
The user responsible for this page is Bea Bleile. No other user may edit this page at present. |
|
This page is being refereed under the supervision of the editorial board. Hence the page may not be edited at present. As always, the discussion page remains open for observations and comments. |
Let 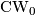 be the category of reduced CW-complexes, that is CW-complexes with
be the category of reduced CW-complexes, that is CW-complexes with  -skeleton a point which is the base-point, and base-point preserving cellular maps. Given an object,
-skeleton a point which is the base-point, and base-point preserving cellular maps. Given an object,  , in
, in 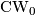 , let
, let 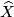 be the universal cover of
be the universal cover of  , and let
, and let 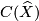 be its cellular chain complex viewed as a complex of left modules over the integer group ring
be its cellular chain complex viewed as a complex of left modules over the integer group ring ![\mathbb Z[\pi_1 X]](/images/math/f/6/3/f63509bcae9a444a3faef44afaa7f90a.png) . To obtain a functor we assume that each object
. To obtain a functor we assume that each object  in
in 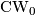 is endowed with a base point in the universal covering
is endowed with a base point in the universal covering 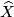 over the base point of
over the base point of  . Then a map
. Then a map 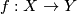 in
in 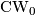 induces a unique base point preserving covering map which, in turn, induces a map
induces a unique base point preserving covering map which, in turn, induces a map 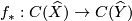 ensuring that
ensuring that 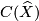 is functorial in
is functorial in  .
.
Given a homomorphism 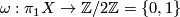 , we define the anti-isomorphism of group rings,
, we define the anti-isomorphism of group rings, ![\overline{\phantom{x}}: {\mathbb Z[\pi_1 X]} \rightarrow {\mathbb Z[\pi_1 X]}](/images/math/d/3/c/d3c2fe3565864188804867fe45220d6f.png) , by
, by 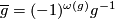 for
for 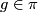 and extending linearly to all of
and extending linearly to all of ![\Zz[\pi]](/images/math/5/9/a/59abcee2c0404c04e89fb508a53c9890.png) . Then, for a left
. Then, for a left ![{\mathbb Z[\pi_1 X]}](/images/math/f/8/3/f83107010b493ba6c140a43f1b1418ec.png) -module,
-module,  , the right module
, the right module 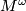 has the same underlying abelian group and action given by
has the same underlying abelian group and action given by 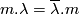 for
for 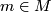 and
and ![\lambda \in \mathbb Z[\pi_1 X]](/images/math/7/d/a/7da2a6383d6130fbeb08695d2011edf9.png) . For
. For 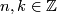 , we put
, we put
Tex syntax error
 (
(Tex syntax error-complex),
![X = (X, \omega_X, [X])](/images/math/2/4/1/241cc76ef5fd0d69aec4b7fe26f19271.png) , consists of an object
, consists of an object  in
in Tex syntax errorwith finitely presented fundamental group
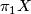 , an orientation character,
, an orientation character, 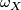 , viewed as a group homomorphism
, viewed as a group homomorphism 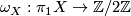 and a fundamental class
and a fundamental class Tex syntax error, such that
Tex syntax error
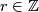 and every left
and every left ![\mathbb Z [\pi_1 X]](/images/math/8/b/6/8b6e4a443a8f7fb3891c745cf136cd4b.png) -module
-module  . An oriented morphism of
. An oriented morphism of Tex syntax error-complexes
![f: (X, \omega_X, [X]) \rightarrow (Y, \omega_Y, [Y])](/images/math/2/5/5/255a1c45683f0c1f2e82c6132c9268de.png) is a morphism
is a morphism 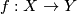 in
in Tex syntax error, such that
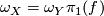 and
and ![f_{\ast}[X] = [Y]](/images/math/b/e/a/bea4c05d0f3c489adcd89e9eefb4fc50.png) . The category
. The category Tex syntax erroris the category consisting of
Tex syntax error-complexes and oriented or degree
 morphisms of
morphisms of Tex syntax error—complexes.
Let
 -types be the full subcategory of the homotopy category
-types be the full subcategory of the homotopy category Tex syntax errorconsisting of
Tex syntax error-complexes
 in
in Tex syntax errorwith
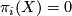 for
for 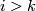 and let
and let
Tex syntax error
 -th Postnikov functor. For
-th Postnikov functor. For  , a fundamental triple
, a fundamental triple 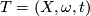 of formal dimension
of formal dimension  consists of an
consists of an  -type
-type  , a homomorphism
, a homomorphism 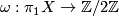 and an element
and an element Tex syntax error. A morphism
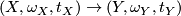 between fundamental triples is a homotopy class
between fundamental triples is a homotopy class 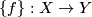 of maps of the
of maps of the  -types, such that
-types, such that 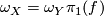 and
and 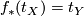 . We obtain the category
. We obtain the category Tex syntax errorof fundamental triples
 of formal dimension
of formal dimension  .
.Every degree
 morphism
morphism 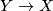 in
in Tex syntax errorinduces a surjection
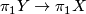 on fundamental groups, see for example [Browder1972a]. The category
on fundamental groups, see for example [Browder1972a]. The category Tex syntax erroris the subcategory consisting of all morphisms inducing surjections on fundamental groups, and we obtain the functor
Tex syntax error
Theorem 1.1.
The functor 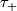 reflects isomorphisms and is full for
reflects isomorphisms and is full for  , that is,
, that is,  is surjective onto sets of morphisms and
is surjective onto sets of morphisms and 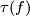 is an isomorphism if and only if
is an isomorphism if and only if  is an isomorphism..
is an isomorphism..
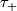 reflects isomorphisms. To show that
reflects isomorphisms. To show that 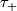 is full requires work. Given
is full requires work. Given Tex syntax error-complexes
 and
and  ,
,  , and a morphism
, and a morphism 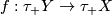 in
in Tex syntax error, we first construct a chain map
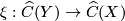 preserving fundamental classes, that is,
preserving fundamental classes, that is, ![\xi_{\ast}[Y] = [X]](/images/math/c/6/4/c6448e8a4adcf8e23031a017eb83065b.png) . Then we use the category
. Then we use the category Tex syntax errorof homotopy systems of order
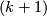 introduced in [Baues1991] to realize
introduced in [Baues1991] to realize  by a map
by a map 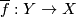 with
with 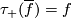 .
.
 . Two
. Two Tex syntax error-complexes are orientedly homotopy equivalent if and only if their fundamental triples are isomorphic.
 by Thomas [Thomas1969], Swarup [Swarup1974], and Hendriks [Hendriks1977], to arbitrary dimension. It also establishes Turaev's conjecture [Turaev1989] on
by Thomas [Thomas1969], Swarup [Swarup1974], and Hendriks [Hendriks1977], to arbitrary dimension. It also establishes Turaev's conjecture [Turaev1989] on Tex syntax error-complexes whose
 -type is an Eilenberg-Mac Lane space
-type is an Eilenberg-Mac Lane space 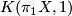 .
Theorem 1.1 also yields a criterion for the existence of a map of degree one between
.
Theorem 1.1 also yields a criterion for the existence of a map of degree one between Tex syntax error-complexes, recovering Swarup's result for maps between
 -manifolds and Hendriks' result for maps between
-manifolds and Hendriks' result for maps between Tex syntax error-complexes.
Special cases of Theorem 1.1 and 1.2 were proved by Hambleton and Kreck [Hambleton&Kreck1988] for 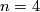 . Teichner extended their approach to the non-oriented case in his thesis [Teichner1992].
Cavicchioli and Spaggiari [Cavicchioli&Spaggiari2001] studied the homotopy type of finite oriented Poincar\'e complexes in even dimensions.
. Teichner extended their approach to the non-oriented case in his thesis [Teichner1992].
Cavicchioli and Spaggiari [Cavicchioli&Spaggiari2001] studied the homotopy type of finite oriented Poincar\'e complexes in even dimensions.
Tex syntax error-complex,
 , is completely determined by its quadratic form. The
, is completely determined by its quadratic form. The  -type of such an
-type of such an  , with
, with 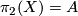 , is an Eilenberg-Mac Lane space
, is an Eilenberg-Mac Lane space Tex syntax errorwith
Tex syntax error. The image of the fundamental class,
![[X]](/images/math/b/6/9/b697f334e90f4eaaec7edab7dc1a384c.png) , under the secondary boundary homomorphism in Whitehead's Certain Exact Sequence is the quadratic form of
, under the secondary boundary homomorphism in Whitehead's Certain Exact Sequence is the quadratic form of  . Hence, in this case, the functor,
. Hence, in this case, the functor,  , coincides with the functor
, coincides with the functor Tex syntax errorof Theorem 2.1.8 in [Baues2003].
 ,
, Tex syntax error-complexes
 and
and  and a map
and a map 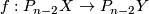 , there is a degree
, there is a degree  map,
map, 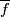 , rendering
, rendering
![\displaystyle \xymatrix{ X \ar[r]^-{p_{n-2}} \ar@{..>}[d]_{\overline f} & P_{n-2}X \ar[d]^f \\ Y \ar[r]^-{p_{n-2}} & P_{n-2}Y}](/images/math/9/8/c/98c15ca585831a4015f3e759ad7312a5.png)
homotopy commutative, if and only if  induces a surjection on fundamental groups, is compatible with the orientations
induces a surjection on fundamental groups, is compatible with the orientations 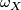 and
and 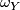 , that is,
, that is, 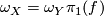 , and
, and
![\displaystyle f_{\ast}p_{n-2 \ast}[X] = p_{n-2 \ast}[Y].](/images/math/9/7/7/97700d99e1f786afe00d3335c4f082d7.png)
Corollary 1.3 is Corollary 3.3 in [Baues&Bleile2008].
Tex syntax error-complex
 , let
, let Tex syntax errorbe the group of oriented homotopy equivalences of
 in
in Tex syntax errorand
Tex syntax errorthe group of automorphisms of the triple
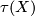 in
in Tex syntax error. Then the latter is a subgroup of
Tex syntax errorand there is a surjection of groups
Tex syntax error
Corollary 1.4 is included in Corollary 4.4 in [Baues&Bleile2008].
 , let
, let ![[\frac{n}{2}]](/images/math/c/e/3/ce35bed745e577a468dbf05fc57b225e.png) be the integer part of
be the integer part of 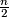 . Associating with a
. Associating with a Tex syntax error-complex,
 , the pre-fundamental triple
, the pre-fundamental triple ![(P_{[\frac{n}{2}]}X, \omega_X, p_{[\frac{n}{2}]\ast}[X])](/images/math/d/2/6/d2646516bef77dcdf2d18fbdf672add9.png) , an orientation preserving map between
, an orientation preserving map between Tex syntax error-complexes is a homotopy equivalence if and only if the induced map between pre-fundamental triples is an isomorphism. However, pre-fundamental triples do not determine the homotopy type of a
Tex syntax error-complex, as is demonstrated by the fake products
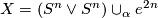 , where
, where  is the sum of the Whitehead product,
is the sum of the Whitehead product, ![[\iota_1 , \iota_2]](/images/math/a/c/d/acd39e7ffdf87edd607e66cb5ca4d891.png) , of the inclusions of the factors in the wedge product, and an element
, of the inclusions of the factors in the wedge product, and an element 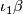 with a non-trivial element
with a non-trivial element 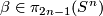 having trivial Hopf invariant. Pre-fundamental triples coincide with the fundamental triple for
having trivial Hopf invariant. Pre-fundamental triples coincide with the fundamental triple for 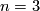 and
and 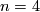 . It remains an open problem to enrich the structure of a pre-fundamental triple to obtain an analogue of Theorem 1.2.
. It remains an open problem to enrich the structure of a pre-fundamental triple to obtain an analogue of Theorem 1.2. 1 References
- [Baues&Bleile2008] H. J. Baues and B. Bleile, Poincaré duality complexes in dimension four, Algebr. Geom. Topol. 8 (2008), no.4, 2355–2389. MR2465744 (2010b:57028) Zbl 1164.57008
- [Baues1991] H. J. Baues, Combinatorial homotopy and
 -dimensional complexes, Walter de Gruyter & Co., 1991. MR1096295 (92h:55008) Zbl 0716.55001
-dimensional complexes, Walter de Gruyter & Co., 1991. MR1096295 (92h:55008) Zbl 0716.55001
- [Baues2003] H. Baues, The homotopy category of simply connected 4-manifolds, Cambridge University Press, 2003. MR1996198 (2004g:57039) Zbl 1039.55009
- [Browder1972a] W. Browder, Poincaré spaces, their normal fibrations and surgery, Invent. Math. 17 (1972), 191–202. MR0326743 (48 #5086) Zbl 0244.57007
- [Cavicchioli&Spaggiari2001] A. Cavicchioli and F. Spaggiari, On the homotopy type of Poincaré spaces, Ann. Mat. Pura Appl. (4) 180 (2001), no.3, 331–358. MR1871619 (2002k:57053) Zbl 1034.57020
- [Hambleton&Kreck1988] I. Hambleton and M. Kreck, On the classification of topological
 -manifolds with finite fundamental group, Math. Ann. 280 (1988), no.1, 85–104. MR928299 (89g:57020) Zbl 0616.57009
-manifolds with finite fundamental group, Math. Ann. 280 (1988), no.1, 85–104. MR928299 (89g:57020) Zbl 0616.57009
- [Hendriks1977] H. Hendriks, Obstruction theory in
 -dimensional topology: an extension theorem, J. London Math. Soc. (2) 16 (1977), no.1, 160–164. MR0454980 (56 #13222) Zbl 03605632
-dimensional topology: an extension theorem, J. London Math. Soc. (2) 16 (1977), no.1, 160–164. MR0454980 (56 #13222) Zbl 03605632
- [Milnor1958] J. Milnor, On simply connected
 -manifolds, Symposium internacional de topología algebraica International symposi um on algebraic topology, Universidad Nacional Autónoma de México and UNESCO, Mexico City (1958), 122–128. MR0103472 (21 #2240) Zbl 0105.17204
-manifolds, Symposium internacional de topología algebraica International symposi um on algebraic topology, Universidad Nacional Autónoma de México and UNESCO, Mexico City (1958), 122–128. MR0103472 (21 #2240) Zbl 0105.17204
- [Swarup1974] G. A. Swarup, On a theorem of C. B. Thomas, J. London Math. Soc. (2) 8 (1974), 13–21. MR0341474 (49 #6225) Zbl 0281.57003
- [Teichner1992] P. Teichner, Topological 4-manifolds with finite fundamental group PhD Thesis, University of Mainz, Germany, Shaker Verlag 1992, ISBN 3-86111-182-9.
- [Thomas1969] C. B. Thomas, The oriented homotopy type of compact
 -manifolds, Proc. London Math. Soc. (3) 19 (1969), 31–44. MR0248838 (40 #2088) Zbl 0167.21502
-manifolds, Proc. London Math. Soc. (3) 19 (1969), 31–44. MR0248838 (40 #2088) Zbl 0167.21502
- [Turaev1989] V. G. Turaev, Three-dimensional Poincaré complexes: homotopy classification and splitting, Mat. Sb. 180 (1989), no.6, 809–830, translation in Math. USSR-Sb. 67 (1990), 261–282. MR1015042 (91c:57031) Zbl 0717.57008
- [Wall1967a] C. T. C. Wall, Poincaré complexes. I, Ann. of Math. (2) 86 (1967), 213–245. MR0217791 (36 #880)
- [Whitehead1949] J. H. C. Whitehead, On simply connected,
 -dimensional polyhedra, Comment. Math. Helv. 22 (1949), 48–92. MR0029171 (10,559d) Zbl 0039.39503
-dimensional polyhedra, Comment. Math. Helv. 22 (1949), 48–92. MR0029171 (10,559d) Zbl 0039.39503
2 External links
- The Encyclopedia of Mathematics article about Poincaré complexes
- The Wikipedia page about Poincaré complexes
- Poincaré complex in n-Lab