Orientation character
|
The users responsible for this page are: Daniel Kasprowski, Christoph Winges. No other users may edit this page at present. |
|
This Definitions page is being reviewed under the supervision of the editorial board. Hence the page may not be edited at present. As always, the discussion page remains open for observations and comments. |
Contents |
1 Definition
Let  be a connected topological manifold throughout.
The following definition can be found in [Davis&Kirk2001, Section 5].
The orientation character is a homomorphism
be a connected topological manifold throughout.
The following definition can be found in [Davis&Kirk2001, Section 5].
The orientation character is a homomorphism
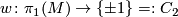
which may be defined as follows. Take the orientation covering 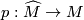 and let
and let 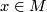 be the base point with lifts
be the base point with lifts 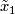 and
and 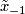 in
in 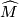 .
For a loop
.
For a loop ![\gamma \colon ([0, 1], \{0, 1\}) \to (M, x)](/images/math/a/e/b/aeb2bc492307160daa03d04a83a540f3.png) based at
based at  ,
let
,
let ![\tilde \gamma \colon [0, 1] \to M](/images/math/1/5/c/15cac579d1f09184b4a1765132c3ab09.png) be the lift of
be the lift of 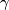 with
with 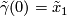 and define
and define  on the homotopy class of
on the homotopy class of 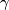 by
by
![\displaystyle w([\gamma]) := \left\{ \begin{array}{rl} 1~~ & \text{if $\tilde{\gamma}(1) = \tilde x_1$,} \\ -1~~ & \text{if $\tilde{\gamma}(1) = \tilde x_{-1}$.} \end{array} \right.](/images/math/f/8/7/f876d7ea45e9d6ecec88e6185fb5d558.png)
The orientation character 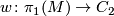 induces a map
induces a map 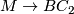 from
from  to the classifying space of
to the classifying space of 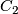 ,
which is unique up to homotopy. By the definition of the orientation character, this map classifies the orientation covering.
So
,
which is unique up to homotopy. By the definition of the orientation character, this map classifies the orientation covering.
So  is trivial if and only if
is trivial if and only if 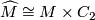 , and therefore
, and therefore  is orientable.
is orientable.
2 Alternative descriptions
Let 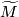 be the universal covering of
be the universal covering of  . Then
. Then 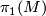 acts on
acts on 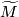 by deck transformations.
by deck transformations.
Proposition 2.1.
Let 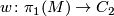 be the orientation character. Then
be the orientation character. Then ![w([\gamma])=1](/images/math/1/e/c/1ec1b0635b602345a2c40d159a4420de.png) if and only if the action of
if and only if the action of ![[\gamma]](/images/math/a/7/7/a7704c0624b013e1ae49d39783fe8a76.png) on
on 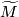 is orientation preserving.
is orientation preserving.
Proof.
If  is orientable, then an orientation on
is orientable, then an orientation on  induces an orientation on
induces an orientation on 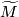 and every deck transformation is orientation preserving.
If
and every deck transformation is orientation preserving.
If  is non-orientable, then the standard orientation of the orientation covering
is non-orientable, then the standard orientation of the orientation covering 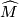 of
of  induces an orientation on
induces an orientation on 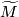 .
By construction the non-trivial deck transformation of
.
By construction the non-trivial deck transformation of 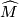 is orientation-reversing. Therefore, a deck transformation of
is orientation-reversing. Therefore, a deck transformation of 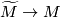 is orientation preserving if and only if it acts trivially on
is orientation preserving if and only if it acts trivially on 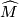 .
.

If the manifold 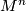 carries a smooth structure, the orientation
character can be additionally characterised in terms of tangential data.
Define a map
carries a smooth structure, the orientation
character can be additionally characterised in terms of tangential data.
Define a map 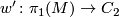 in the
following way:
Let
in the
following way:
Let 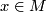 be the base point. Pick a chart
be the base point. Pick a chart 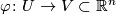 around
around  . Let
. Let 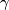 be a based loop in
be a based loop in  .
The standard orientation
.
The standard orientation ![[e_1, \dots, e_n]](/images/math/1/4/7/147b47c0180ac8516262935d6a7bc832.png) of
of 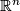 corresponds to an orientation
corresponds to an orientation  of
of 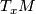 under the differential of
under the differential of
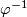 (cf. Orientation of manifolds).
Fibre transport along
(cf. Orientation of manifolds).
Fibre transport along 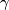 yields another orientation
yields another orientation 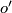 of
of 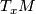 . Now set
. Now set
![\displaystyle w^\prime([\gamma]) := \left\{ \begin{array}{rl} 1~~ & \text{if $o^\prime=o$,} \\ -1~~ & \text{if $o^\prime=-o$.} \end{array} \right.](/images/math/2/9/a/29a864a178dc830d62741382219a360c.png)
Using the comparison between homological and tangential orientation (see Orientation of manifolds), one can show the following:
Proposition 2.2.
The map 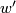 is a well-defined group homomorphism and coincides with the orientation character
is a well-defined group homomorphism and coincides with the orientation character  .
.
In addition to this geometric characterisation, the orientation character also admits a description in terms of characteristic classes:
Under the "evaluation" homomorphism of the Universal Coefficient Theorem  ,
the first Stiefel-Whitney class
,
the first Stiefel-Whitney class 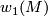 corresponds to a homomorphism
corresponds to a homomorphism
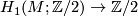 which we also call
which we also call 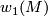 .
.
Proposition 2.3.
Let 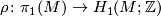 be the Hurewicz homomorphism.
Then the orientation character of
be the Hurewicz homomorphism.
Then the orientation character of  coincides with the composition
coincides with the composition 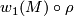 via the canonical isomorphism
via the canonical isomorphism 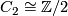 .
.
Proof.
All 1-manifolds are orientable, so suppose that 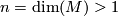 .
Let
.
Let 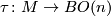 classify the tangent bundle of
classify the tangent bundle of  and consider the induced map
and consider the induced map 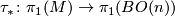 .
Now
.
Now 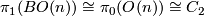 is generated by the classifying map of the Möbius bundle;
denote this class by
is generated by the classifying map of the Möbius bundle;
denote this class by ![[\eta]](/images/math/4/3/0/430fca6222b9927883e05d9c51bc2cb6.png) . Hence, for a based loop
. Hence, for a based loop 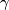 in
in  with homotopy class
with homotopy class ![[\gamma] \in \pi_1(M)](/images/math/9/5/9/959f1927245b6dcdfab80ed32ee9c522.png) ,
we see the pullback
,
we see the pullback 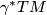 is non-trivial if and only if
is non-trivial if and only if ![\tau_*([\gamma]) = [\eta]](/images/math/8/0/1/801121f4cfc23029ea706cf6b9c4e762.png) .
By Proposition 2.1, we see that
.
By Proposition 2.1, we see that ![w([\gamma]) = 1](/images/math/5/b/6/5b616cdcc399f5cf6c4179755050e7b1.png) if and only if
if and only if ![\tau_*([\gamma]) = [\eta]](/images/math/8/0/1/801121f4cfc23029ea706cf6b9c4e762.png) .
Applying the Universal Coefficient Theorem for
.
Applying the Universal Coefficient Theorem for 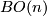 , we see that the universal first Stiefel-Whitney class
, we see that the universal first Stiefel-Whitney class 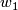 ,
which generates
,
which generates 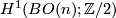 , has the property that
, has the property that ![w_1(\rho([\eta])) = 1](/images/math/c/3/4/c3439a8c9df68619727e1258c8437486.png) .
Hence, we see that
.
Hence, we see that ![w([\gamma]) = 1](/images/math/5/b/6/5b616cdcc399f5cf6c4179755050e7b1.png) if and only if
if and only if ![\tau_*([\gamma]) = [\eta]](/images/math/8/0/1/801121f4cfc23029ea706cf6b9c4e762.png) if and only if
if and only if ![w_1(\rho(\tau_*[\gamma])) = 1](/images/math/d/3/b/d3b0a00376f8ab24ae41c24a7544ae5e.png) if and only if
if and only if ![w_1(M)(\rho([\gamma])) = 1](/images/math/d/8/d/d8d26b0e59f3596b926d89587bc35460.png) .
.

3 Examples
- Since
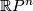 is orientable if and only if
is orientable if and only if  is odd, the orientation character
is odd, the orientation character 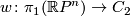 is trivial if and only if
is trivial if and only if  is odd. If
is odd. If  is even,
is even, 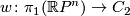 is an isomorphism.
is an isomorphism.
- The open Möbius strip has fundamental group
 and is non-orientable. Therefore, the orientation character is given by the surjection
and is non-orientable. Therefore, the orientation character is given by the surjection 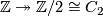 .
.
- If
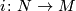 is an embedding of a manifold of the same dimension (possibly with boundary), then the orientation character of
is an embedding of a manifold of the same dimension (possibly with boundary), then the orientation character of  is given as the composition
is given as the composition 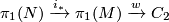 . This follows from the fact that the atlas of
. This follows from the fact that the atlas of  with local orientations induces by restriction an atlas of
with local orientations induces by restriction an atlas of  with local orientations. Therefore, the orientation covering of
with local orientations. Therefore, the orientation covering of  is the orientation covering of
is the orientation covering of  restricted to
restricted to  .
.
- Let
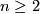 . The preimage of an embedded disk
. The preimage of an embedded disk 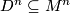 in the orientation covering
in the orientation covering 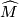 is a disjoint union of two disks. The orientation covering of a connected sum
is a disjoint union of two disks. The orientation covering of a connected sum 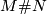 along
along 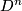 is the "double connected sum" of the orientation coverings along the preimages of
is the "double connected sum" of the orientation coverings along the preimages of 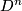 in the orientation coverings. How to pair the disks is determined by the local orientations. From this it follows that the orientation character of
in the orientation coverings. How to pair the disks is determined by the local orientations. From this it follows that the orientation character of 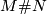 is given by the pushout
is given by the pushout ![\displaystyle \xymatrix{\pi_1(S^{n-1})\ar[r]\ar[d]&\pi_1(M\backslash \text{int}(D^n))\ar[d]\ar[ddr]&\\ \pi_1(N\backslash \text{int}(D^n))\ar[r]\ar[drr]&\pi_1(M\#N)\ar@{-->}[dr]&\\&&C_2}](/images/math/9/0/b/90b87fbed0564c128fcd03a13d3e5967.png)
4 The orientation character via Poincaré duality
Even though the original definition is very geometric, the orientation character is already completely determined by the homotopy type of a given closed manifold. Both the Hurewicz homomorphism and the first Stiefel-Whitney class are homotopy invariants (for the second point, see the Manifold Atlas page Wu class), so we already know this for differentiable manifolds by Proposition 2.3. In general this is most easily seen in the more abstract setting of Poincaré complexes, see [Lück2001, Section 3.1].
Lemma 4.1.
If ![(X, [X], w)](/images/math/2/5/2/252d1554e3a68ed094d5839fd83061f0.png) is a connected Poincaré complex, then
is a connected Poincaré complex, then  is the only homomorphism
is the only homomorphism 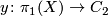 such that
such that  is a Poincaré complex with orientation character
is a Poincaré complex with orientation character  .
.
Proof.
Suppose ![(X,[X],y)](/images/math/b/f/0/bf096de76ba8a56645dcbe8388236295.png) is a connected Poincaré complex. We first introduce some notation:
is a connected Poincaré complex. We first introduce some notation:
-
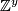 denotes
denotes  as a right
as a right ![\mathbb{Z}[\pi_1(X)]](/images/math/6/0/0/6000cfbde265d4e4a836a3979b050aa4.png) -module, where the
-module, where the 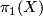 -action is given by
-action is given by 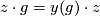 .
.
-
![\mathbb{Z}[\pi_1(X)]^y := \mathbb{Z}^y \otimes_{\mathbb{Z}[\pi_1(X)]}\mathbb{Z}[\pi_1(X)]](/images/math/a/6/d/a6def5f059980446b95cc183260b758f.png) , where the tensor product is equipped with the diagonal action.
, where the tensor product is equipped with the diagonal action.
- For a left
![\mathbb{Z}[\pi_1(X)]](/images/math/6/0/0/6000cfbde265d4e4a836a3979b050aa4.png) -chain complex
-chain complex 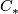 , we define
, we define 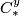 analogous to (2.).
analogous to (2.).
Applying 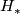 to the
to the ![\mathbb{Z}[\pi_1(X)]](/images/math/6/0/0/6000cfbde265d4e4a836a3979b050aa4.png) -chain equivalence
-chain equivalence ![? \cap [X] \colon C^{n-*}(\widetilde{X}) \to C_*(\widetilde{X})^y](/images/math/7/1/e/71e64e5dad6ab0f03986495d1a717842.png) , we obtain an
isomorphism of
, we obtain an
isomorphism of ![\mathbb{Z}[\pi_1(X)]](/images/math/6/0/0/6000cfbde265d4e4a836a3979b050aa4.png) -modules
-modules
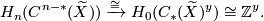
Note that the left hand side is independent of the orientation character  . Therefore,
. Therefore, 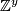 is isomorphic to
is isomorphic to 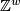 as a
as a ![\Zz[\pi_1(X)]](/images/math/c/4/a/c4a38c87cc533a28127f14739be9ba73.png) -module and
-module and  and
and  have to agree.
have to agree.

Corollary 4.2.
If ![(X, [X], w)](/images/math/2/5/2/252d1554e3a68ed094d5839fd83061f0.png) is a connected Poincaré complex, then
is a connected Poincaré complex, then  depends only on the homotopy type of
depends only on the homotopy type of  .
.
Proof.
Let ![(X,[X],w)](/images/math/5/5/7/557e5cad86ac0ee4f17f0f20bb8001c4.png) and
and ![(X',[X'],w')](/images/math/0/3/6/0363f659e0ef272ed4620361afc14593.png) be connected Poincaré complexes and
be connected Poincaré complexes and 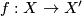 be a homotopy equivalence. Then
be a homotopy equivalence. Then ![(X,[X],w'\circ f_*\colon\pi_1(X)\to C_2)](/images/math/1/9/5/195323937c3df1e9b70ef523668fa4b1.png) is a Poincaré complex and
is a Poincaré complex and  and
and  have to agree.
have to agree.

Remark 4.3. The above statements are also true for connected Poincaré pairs.
Proposition 2.3 generalises to the following:
Proposition 4.4 [Byun1999, Lemma 4.3]. Using the Universal Coefficients Theorem and the Hurewicz map, the orientation character of a connected Poincaré complex coincides with the first Stiefel-Whitney class of its Spivak normal fibration.
5 References
- [Byun1999] Y. Byun, Tangent fibration of a Poincaré complex, J. London Math. Soc. (2) 59 (1999), no.3, 1101–1116. MR1709099 (2000f:57023) Zbl 0935.57032
- [Davis&Kirk2001] J. F. Davis and P. Kirk, Lecture notes in algebraic topology, American Mathematical Society, 2001. MR1841974 (2002f:55001) Zbl 1018.55001
- [Lück2001] W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020
6 External links
- The Wikipedia page about the orientation character