Whitehead torsion V (Ex)
(Difference between revisions)
m |
m |
||
| Line 2: | Line 2: | ||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
# Show that the operations (1)-(5) from {{citeD|Lück2001|Section 1.4}} used in the definition of the Whitehead group in fact yield equivalence classes of invertible matrices of arbitrary size. | # Show that the operations (1)-(5) from {{citeD|Lück2001|Section 1.4}} used in the definition of the Whitehead group in fact yield equivalence classes of invertible matrices of arbitrary size. | ||
| + | # Show that addition is well-defined in the Whitehead group via | ||
| + | $$ [A] + [B] = \left [\begin{array}{cc} A & 0 \\ 0 & B \end{array} \right] = [(A) \cdot (B \oplus \text{Id}_{n-m})].$$ | ||
| + | Here $A$ is an $n \times n$ matrix, $B$ is an $m \times m$ matrix with $n \geq m$, $O$ denotes the zero $n \times m$ and $m \times n$ matricies and $\cdot$ denotes matrix multiplication. | ||
# Show that $Wh(e)$ is trivial. | # Show that $Wh(e)$ is trivial. | ||
{{endthm}} | {{endthm}} | ||
Revision as of 12:13, 26 March 2012
Exercise 0.1.
- Show that the operations (1)-(5) from [Lück2001, Section 1.4] used in the definition of the Whitehead group in fact yield equivalence classes of invertible matrices of arbitrary size.
- Show that addition is well-defined in the Whitehead group via
![\displaystyle [A] + [B] = \left [\begin{array}{cc} A & 0 \\ 0 & B \end{array} \right] = [(A) \cdot (B \oplus \text{Id}_{n-m})].](/images/math/0/f/8/0f8cc51d28a38b2f28c06a0e40d79f83.png)
Here  is an
is an 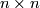 matrix,
matrix,  is an
is an 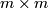 matrix with
matrix with 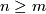 ,
, 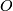 denotes the zero
denotes the zero 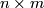 and
and 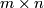 matricies and
matricies and  denotes matrix multiplication.
denotes matrix multiplication.
- Show that
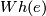 is trivial.
is trivial.
The exercises and hints on this page were sent by Alex Koenen and Arkadi Schelling.