Wall realisation (Ex)

Exercise 0.1. Given a compact $<wikitex>; {{beginthm|Exercise}} Given a compact n-1$-manifold $X$ show that we can attach two $n$-handles to $X \times I$ in such a way that the geometric intersection number of immersed spheres representing these handles (i.e. the upper hemisphere, say, is given by the core of the handle und the lower on by a map into $X \times I$) is $\pm g$ for a given $g \in \pi_1(X,(b,0))$, where $b \in X$ is some fixed point. \ Hint: Such a construction is sketched in L¸ck's Article on pages 115 - 116 (and in our talk), all that remains to be checked is the signs. {{endthm}} {{beginrem|Hint}} Assume that the cores of the handles are homotopic in $X \times I$. 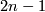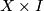{{endrem}} </wikitex> == References == {{#RefList:}} [[Category:Exercises]]2n-1$-manifold $X$ show that we can attach two $n$-handles to $X \times I$ in such a way that the geometric intersection number of immersed spheres representing these handles (i.e. 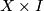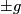the upper hemisphere, say, is given by the core of the handle und the lower on by a map into $X \times I$) is $\pm g$ for a given 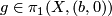$g \in \pi_1(X,(b,0))$, where 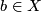$b \in X$ is some fixed point.

Hint 0.2. Such a construction is sketched in [Lück2001, pp.115 - 116] all that remains to be checked is the signs. In particular, you may assume that the attaching spheres of the $n$-handles are homotopic in 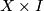$X \times I$.